"MooseGesture" - Python Mouse Gestures Module
Posted by Al Sweigart in misc
"MooseGesture" is a Python module that implements a basic mouse gesture recognition system. It can identify gestures made up of strokes in the eight cardinal and diagonal directions.
A mouse gesture is holding down the mouse button and moving the mouse cursor in a specific pattern to issue a command.
Mouse gestures are a way of dragging with the mouse in order to draw out a certain pattern. The most mainstream uses of mouse gestures in computer software are for web browsers. (Chrome, Firefox, Opera, Internet Explorer)
Mouse gestures can provide an interesting game mechanic that you can add to your own programs (similar to what the Wiimote does in a few games).
You can download the module (and a simple Pygame test script that uses it) here:
MooseGestures & Test App (zipped)
Simon Gesture - A game that uses the MooseGesture module.
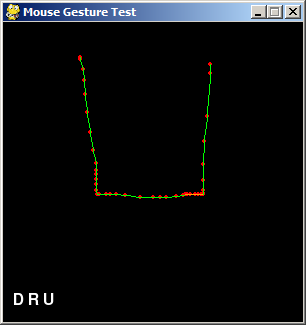
(The screenshot above shows the test app after entering a mouse gesture. It correctly identifies the gesture as Down Right Up.)
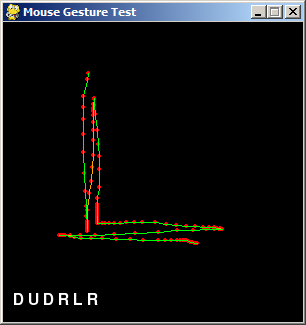
(The above screenshot shows a more complicated gesture: Down, Up, Down, Right, Left, Right.)
Description of the Algorithm
First, some nomenclature (at least how I use it):
- A "point" is a 2D tuple of x, y values. These values can be ints or floats, MooseGesture supports both.
- A "point pair" is a point and its immediately subsequent point, i.e. two points that are next to each other.
- A "segment" is two or more ordered points forming a series of lines.
- A "stroke" is a segment with all its point pairs going in a single direction (one of the 8 cardinal or diagonal directions: up, upright, left, etc.)
- A "gesture" is one or more strokes in a specific pattern, e.g. up then right then down then left.
The identification of strokes is based on a simple slope calculation between two points. MooseGesture can identify several strokes in a row in the eight cardinal and diagonal directions (up, down, left, right, and the four diagonals in between). MooseGesture does not recognize two strokes in the same direction performed in succession, but sees it as just one stroke in that direction. So up, up, down, down, left, right, left right would be identified as just up, down, left, right.
A slope is calculated between two XY coordinates with the basic "rise over run" calculation: (y2 - y1) / (x2 - x1)
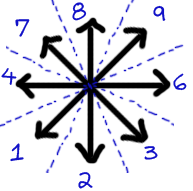
The slope is then categorized into one of the eight directions by checking which "zone" it falls into. Each of the eight zones spans 45 degrees. To make it easier to remember, I've numbered them according to the same directions the numbers on your keyboard's number pads align to:
The key is to know when one stroke ends and another begins, and to allow for some inaccuracy and imperfection from the user. MooseGesture does this by breaking up the user's gesture into overlapping "segments" and testing for a consistent direction on all point pairs in that segment.
Here's what I mean. Say the user's gesture (which is just an ordered list of XY points) looks like this:
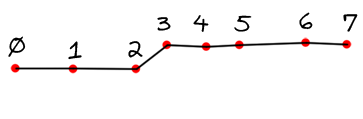
The user intends to just have a simple to-the-right gesture, but because of some natural shaky mouse movement there is a little deviation in it. We want this deviation to be ignored, and not identified as an additional upright stroke. The segment consistency checks in our algorithm will ignore these little bumps.
A "segment" has a starting point, and then continues to include subsequent points until it meets a minimum segment length (and no longer). (The minimum segment length is adjustable. A smaller minimum segment length lets strokes be shorter but increases the odds of misidentified strokes.) So say the gesture has 10 points (which we'll call 0 to 9) altogether. The first segment starts at point 0 and goes on for some number of points until it is at least the minimum segment length. The second segment starts at point 1. This means that the second segment overlaps the first for a bit. (This depends on the lengths of the segments, which depends on how close together/far apart the points are.)
The last segment will start at the latest point that we can get a segment that meets the minimum segment length. So if the distance between points 7 to 8 to 9 is less than the minimum segment length, there won't be a segment that starts at point 7 (or, logically, at point 8).
Note that the length of a segment is the sum of lengths of its point pairs, not the distance between the first and last points in the segment. For example, the distance between points 0 and 1, 1 and 2, and 2 and 3. It would not be the distance between points 0 and 3.
Here's an animated gif that shows a gesture with 8 points (0 to 7), with the segments highlighted in turn:
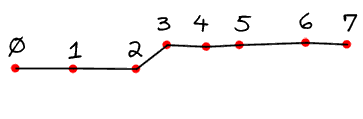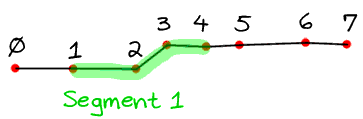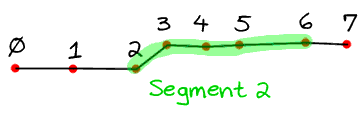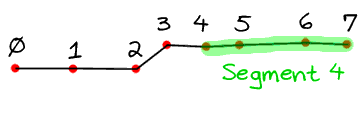
The Algorithm:
- Split up the gesture's points into segments that meet the minimum segment length.
- For each segment: Calculate the slope of each point pair and categorize them into one of the eight directions based which "zone" the slope falls in.
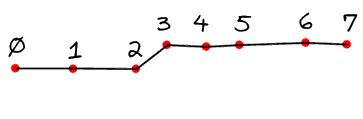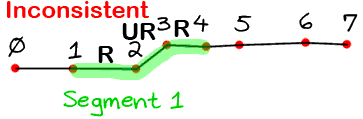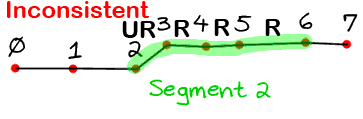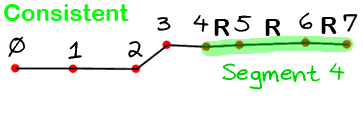
- If all of the point pairs in the segment agree on the direction, then this segment is considered consistent and the direction is added to the list of identified strokes. See the animated gif below for an example of consistent/inconsistent segments, the R stands for "right direction point pair" and the UR for "upright direction point pair".
- The list of identified strokes is returned as the identified gesture.
(There is one exception to adding a consistent segment: if the previously identified stroke is in the same direction as this one, then we don't add the direction. This prevents multiple sequential strokes in the same direction, i.e. up-up-up-left-left is just considering up-left.)
This algorithm lets us ignore tiny deviations because they will create an inconsistent segment (i.e. a segment wit pair points going in different directions. So we drop that segment from being considered an identified stroke. But there is bound to be some segments before and after it that are consistent.
One limitation is that MooseGesture can only identify direction. It can't identify lengths or specific shapes. So these two paths are both interpreted as the same gesture by MooseGesture (upright, downright, left):
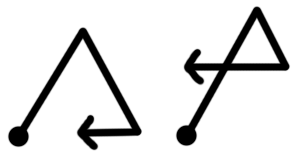
This is just an algorithm that I came up with literally over a weekend. Even for gestures with an absurd number of points in them, it seems to run in a couple milliseconds. It can probably be improved, but will work just fine for most Python games. I'll be converting the module to JavaScript in the future. Email me any questions you might have. Enjoy!




