Recursion Explained with the Flood Fill Algorithm (and Zombies and Cats)
Posted by Al Sweigart in misc
This is a programming tutorial for beginner and intermediate programmers who want to learn what recursion is. The programming language used for the examples is Python, but you can probably follow along if you know programming in some other language such as PHP or JavaScript. There’s a lot more information about recursion on the Wikipedia article: http://en.wikipedia.org/wiki/Recursion_(computer_science) But this guide is meant to be a more practical guide to show how handy recursion is.
The source code of everything in this article can be downloaded here: floodfill_src.zip
Consider the Lazy Zombie
This is a cat:

This is a normal human:

This is a normal human who has been turned into an ungodly, flesh-eating zombie of the undead:

Zombies are lazy and will only bite things that are next to them. Humans that are bitten will then turn into zombies:

There is an interesting recursive principle here, because the humans that have turned into zombies will start to bite other humans that are next to them, which will make more zombies, who bite more adjacent humans, which will make more zombies, and so on and so on in a chain reaction:

Zombies don’t bite cats though. (Well, they do, but a zombie-bitten cat won’t turn into a zombie.) If you put a zombie next to a cat, you’ll just end up with a zombie and a cat:

So as long as there is a cat between the human and the lazy zombie, the human is safe:

The same cannot be said of any humans who don’t have a cat between them and a zombie:

So not only does this simple lazy-zombie principle cause a chain reaction of zombies, it also causes this chain reaction to stop when a cat is encountered. (Public Service Announcement: In the event of a zombie apocalypse, please locate your local crazy cat person for safety and shelter.)

Let’s make a two dimensional field of humans, cats, and zombies like this:

All we need is one starting zombie, and you’ll see the infection spread until the entire human population is zombified. But there’s hope. If there is an enclosed ring of cats blocking the initial zombie, then humanity is (slightly) saved. (In our example, zombies don’t bite diagonally.)

But if there is a gap in the cats, then the entire population is doomed:

This whole zombie thing is an elaborate and silly analogy for the flood fill algorithm.
The Basics: Recursive Calls and Base Cases
A recursive function is simply a function that calls itself. Here’s the simplest possible recursive function:
def foo():
foo()
The foo() function does nothing but call itself. The function doesn’t do anything useful (well, it will crash your program. That's kind of like being useful.) A recursive function's function call to itself is a recursive call.
Here's a program that calls this pointless recursive function:
def foo(): foo() foo()
You can download it here: stackoverflow.py If you run this program, you'll get this error message: “RuntimeError: maximum recursion depth exceeded” (This is called a "stack overflow" and is explained later.) Stack overflows happen when a recursive function doesn't have a base case (explained next).
Here's a relatively more useful recursive function:
def countdown(n):
print(n)
if n == 0: # this is the base case
return # return, instead of making more recursive calls
countdown(n - 1) # the recursive call
countdown(10)
You can download this program here: simplerecursion.py. When you run this program, the countdown() function is called and passed the integer 10 for the n parameter. The function will print this number, and then later call itself but pass the integer 9 (which is what n - 1 is). That second call to countdown results in 9 being printed to the screen, and then calls itself and passes 8. This keeps going until countdown() is called with an n parameter of 0. Then it just returns to the function which called it, which is the countdown() function. That function then returns to the function that called it (also the countdown() function) and the program keeps returning until it has returned from the original countdown() function call.
The condition that a recursive function will stop making recursive calls to itself is called the base case.
A Stupid Recursive Example: Fibonacci Sequence
The recursion property can do some pretty cool and powerful things. Most textbook examples of recursion show the Fibonacci sequence. The Fibonacci sequence is a sequence of numbers that begins with the numbers 1 and 1, and then each number afterwards is the sum of the two previous numbers:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55 and so on…
A recursive function to calculate the Nth number of the Fibonacci sequence that is typed into Python’s interactive shell would look like this:
>>> def getFib(n): ... if n == 1 or n == 2: ... return 1 ... return getFib(n-1) + getFib(n-2) ... >>> getFib(4) 3 >>> getFib(10) 55 >>>
This works because to calculate getFib(5), you just add the results of getFib(4) and getFib(3) (and those in turn make more calls to getFib() until they reach the base case where getFib(1) or getFib(2) is called.) A good indicator that you can perform a task by using recursion is that the task can be divided into identical smaller sub-tasks. The Nth Fibonacci number can be calculated by calculating the N-1 and N-2 Fibonacci numbers, which themselves can be calculated by finding other Fibonacci numbers, until you reach the base case of having to calculate the 1st or 2nd Fibonacci numbers (which are both just 1.)
But this is a stupid example of recursive functions. You could have easily written an iterative (that is, non-recursive) function to do the same thing:
>>> def getFib(n): ... a = 1 ... b = 1 ... i = 3 ... while i <= n: ... c = a + b ... a = b ... b = c ... i = i + 1 ... return b ... >>> getFib(10) 55 >>>
The iterative function is a little bit longer, but it does the exact same thing as the recursive version and is probably easier to understand. This stupid example doesn’t show the power of recursion very well. Why learn recursion when straightforward iterative approach works just as well? Consider the flood fill problem, which does not have an obvious non-recursive solution...
Flood Filling
Flood filling is when you want to change the color of an area of color in an image. It’s available in a lot of graphics programs and usually looks like a paint bucket being tilted over, like this:
![]()
For example, if we flood fill a circle, the change will look like this (the blue dot indicates where the flood filling starts):
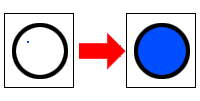
The blue flood filling starts at that blue point (which was originally white), so it will keep spreading as long as it finds adjacent white pixels. Imagine it as blue paint pouring on that dot, and it keeps spreading until it hits any non-white colors (like the black circle). If we started the flood filling from the outside of the circle, then the entire outside area would be filled up instead:
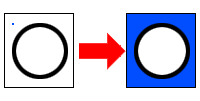
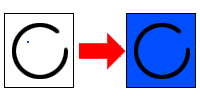
Flood filling a circle that is not completely enclosed wouldn’t work the same way. The flood filling color would “leak out” the open space in the circle and then fill up the outside space as well:
The really clever thing about flood fill is that it can fill up any arbitrary enclosed shape:
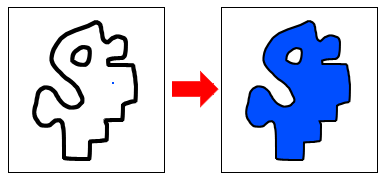
The image on your screen is nothing but individual squares of color called pixels. In order to change the color of the pixels, our function will have to calculate the X and Y coordinates of each pixel that needs to be changed. It isn’t really obvious how to do that. There are so many different possible shapes, so how can we write one function that will handle all the possible shapes there are?
Let’s write some code that does this. Here’s some simple pseudocode of a flood fill function:
def floodfill(x, y, oldColor, newColor): # assume surface is a 2D image and surface[x][y] is the color at x, y. if surface[x][y] != oldColor: # the base case return surface[x][y] = newColor floodfill(x + 1, y, oldColor, newColor) # right floodfill(x - 1, y, oldColor, newColor) # left floodfill(x, y + 1, oldColor, newColor) # down floodfill(x, y - 1, oldColor, newColor) # up
In this pseudocode example, surface[x][y] represents a pixel on some drawing surface (such as a window) of different pixels. You call the floodfill() function once with an X and Y coordinate, the color of the pixel you want to flood, and the new color that will flood the surface.
If the X and Y coordinate on the surface matches the old color, it changes it to the new color. Not only that, but it will then call floodfill() on the pixel to its right, left, down, and up direction. It doesn’t matter what order these pixels are called, the result will always be the same. If those neighboring pixels are also the same as the old color, then the process starts all over again (just like a human turned into a zombie will begin biting all the neighboring humans). Those floodfill() calls will make other floodfill() calls, until they finally all return to the original floodfill() call, which itself returns. The surface will then have the old color flooded with the new color.
Notice that our flood fill function has four recursive calls each time it is called. (Our countdown function only had one recursive call each time it was called.) This is fine. Some recursive algorithms just use different numbers of recursive function calls in their recursive functions.
The base case for flood fill is when a different color (or the edge of the image) is encountered. That's when the recursive calls stop.
Text Flood Fill
Here's a Python program that implements the flood fill algorithm with a 2D text field: recursivefloodfill.py
The text field in the program (which you can change yourself to play around with) originally looks like this:
.................... .......XXXXXXXXXX... .......X........X... .......X........X... ..XXXXXX........X... ..X.............X... ..X.............X... ..X........XXXXXX... ..X........X........ ..XXXX..XXXX........ .....XXXX........... .................... ....................
The program than starts flood filling at the coordinate (5, 8) (which is inside the outline of X's) with the + character. The floodFill() function sees that the character at (5, 8) is a period, so it will then recursive call itself on the neighboring coordinates and as long as these calls find a period at those coordinates, they will change it to a plus sign and continue to make recursive calls. The base case that stops more recursive calls is when a non-period character is found. The text field then looks like this:
.................... .......XXXXXXXXXX... .......X++++++++X... .......X++++++++X... ..XXXXXX++++++++X... ..X+++++++++++++X... ..X+++++++++++++X... ..X++++++++XXXXXX... ..X++++++++X........ ..XXXX++XXXX........ .....XXXX........... .................... ....................
Then the floodFill() function is called again, this time on the coordinate (0, 0) (which is the top left corner of the field, and outside the X's) with the s character. The text field then looks like this:
ssssssssssssssssssss sssssssXXXXXXXXXXsss sssssssX++++++++Xsss sssssssX++++++++Xsss ssXXXXXX++++++++Xsss ssX+++++++++++++Xsss ssX+++++++++++++Xsss ssX++++++++XXXXXXsss ssX++++++++Xssssssss ssXXXX++XXXXssssssss sssssXXXXsssssssssss ssssssssssssssssssss ssssssssssssssssssss
The program that does the text flood fill can be downloaded here: recursivefloodfill.py
Room Counting Program
This flood fill technique can be very useful for different problems. Imagine that you had some text that represented a map of different walls in a space. The #’s represent the walls. Given this as input, how can you find out how many intact rooms are in the data? For example, here's one possible map with four rooms (the wall that does not form a closed off room does not count as a room):
........................#..... ........................#..... ........................#..... .....######.............###### .....#....#....######......... .....#....#....#....#.....#... .....######....##.###.....#... ................#.#.......#### ................#.#........... ######.....######.#######..... #....#.....#............#..... ###..#.....#............#..... ###..#.....##############..... #....#........................ ######........................
You can use flood fill to find out the answer. Just perform the flood fill algorithm on every possible empty space (in this case, the empty spaces are represented by periods). The number of rooms will be the number of times you find an empty space, minus one (since the area outside of all rooms will count as a “room”.)
You can download a program that implements our room counting function here: roomcounter.py You can modify the textmap variable to experiment with the function.
Flood filling the empty spaces will mark the map so that we know if we’ve already marked a room before.
Sierpinski Triangles
Another example of a recursive function is a function that will draw Sierpinski triangles. A Sierpinski triangle simply is a triangle with an upside down triangle inside of it. This forms three other triangles (one on the top center, bottom left, and bottom right). It looks like the Triforce from the Legend of Zelda games.
Drawing several levels of Sierpinski triangles is a recursive job. First you draw one Sierpinski triangle, and then you draw three more smaller Sierpinkski triangles, one in each of the three sub-triangles. Then you draw three more Sierpinski triangles each of the three sub-triangles in each of the three sub-triangles, and so on. Each level of drawing multiplies the total number of triangles by three. So 4 levels means 3 * 3 * 3 * 3 = 3^4 = 81 triangles. Seven levels of Sierpinski triangles would create 3^7 or 2,187 triangles. Here’s an animation of a new layer of Sierpinski triangles being drawn:

This animation maxes out at the 7th recursive level, since by then the sub-triangles become smaller than one pixel and can’t be drawn. (If the triangle looks a little funny, that’s because slight rounding errors happen once the triangles get so tiny.) The program that generates this animation is here: sierpinski.py (this requires Pygame to be installed.)
A Sierpinski triangle is known as a fractal, which are shapes that are composed of smaller, self-similar shapes. Recursion is naturally suited for making fractal pictures, which look pretty cool. There's a bunch of cool looking examples on the Wikipedia page for fractals: http://en.wikipedia.org/wiki/Fractal
Recursion is at the base of fractals, and fractals are at the base of terrain generation algorithms. Many games don't have programmers design mountains by individually setting each polygon that makes up a mountain or hilly grassland. Instead they use a terrain generation algorithm (which is a bit too detailed to go into in this article. Check out the Wikipedia page: http://en.wikipedia.org/wiki/Fractal_landscape )
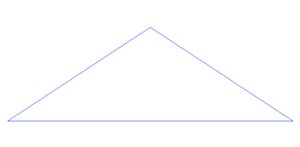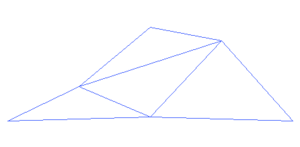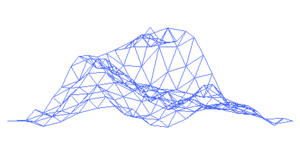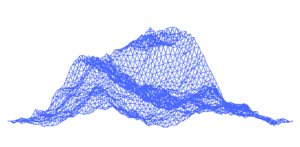
Recursion is Just a Fancy Way of Using a Stack
A stack is just like an array or a list, with one exception: items can only be added or removed from the very end of the stack. (Although when stacks are drawn out, people usually draw them vertically and things are only added or removed from the top of the stack. Think of a stack of plates.) It’s a very basic computer science data structure, and one that the computer actually uses at a low level. Programming languages just add a bunch of fancy features and manipulation of low level data structures (such as Python’s lists, dictionaries, or things like lists that contain lists) so that it is easier to write programs.
Some detailed info about stacks can be found on the Wikipedia page: http://en.wikipedia.org/wiki/Stack_(data_structure)
Think about what happens when your program calls a function. The execution jumps from the line of code that is calling the function and to the first line of code inside the function. After the function returns, the execution jumps back to the line after the calling line. If your programs calls a function named foo() which calls another function named bar(), the program’s execution will finish running bar(), jump back to the line in foo() that called bar(), finish running foo(), and then return back to the line that called foo().
How does Python remember which line to jump back to when it returns from a function? It uses a stack. Look at this simple program which we described earlier:
def foo():
bar()
def bar():
print('Hello')
foo()
This program calls foo(), which calls bar(), which then returns back to foo(), which then returns back to the line that called foo(). Every time a function is called, the line calling the function is saved to the stack. When a function returns, the item at the top of the stack is removed. Adding an item to the top of the stack is called “pushing” an item onto the stack. Removing an item from the top of the stack is called “popping” an item off the stack. If we drew out the “stack”, it would look like this:
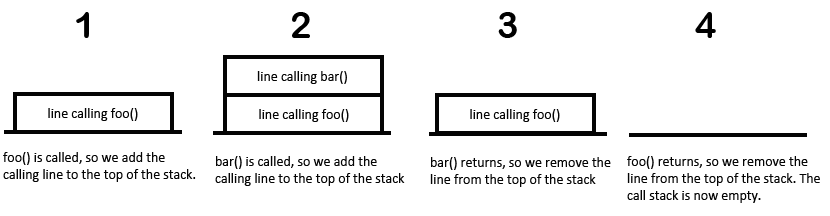
If you called a function that called a function that called a function that called a function, this is how Python keeps track of where to return to whenever a function returns. This stack is called the “call stack”. (It’s also sometimes called an execution stack or run-time stack.) The Wikipedia page for call stacks is here: http://en.wikipedia.org/wiki/Call_stack
The call stack is stored in the computer’s memory. It cannot become infinitely large because no computer has an infinite amount of memory. So when a recursive function has a bug and never reaches a base case, eventually the computer runs out of memory and crashes the program. This is called a “stack overflow”. In Python, a stack overflow error looks like this: “RuntimeError: maximum recursion depth exceeded”
Hey, instead of implicitly using the call stack when we have recursive functions, why don’t we just use our own stack structure instead? Then we could implement the flood fill algorithm without this complicated recursion stuff. (This is generally a bad idea. Recursion is really useful once you get used to them, and much easier than making your own data structure. But this example here is just to show how recursion is really just a nifty use of a stack data structure.)
Here’s an example. Notice the addition of a list (which we use as a stack) and the lack of recursive function calls (i.e. the floodfill() function never calls floodfill()):
def floodfill(x, y, oldColor, newColor): # assume surface is a 2D image and surface[x][y] is the color at x, y. theStack = [ (x, y) ] while len(theStack) > 0: x, y = theStack.pop() if surface[x][y] != oldColor: continue surface[x][y] = newColor theStack.append( (x + 1, y) ) # right theStack.append( (x - 1, y) ) # left theStack.append( (x, y + 1) ) # down theStack.append( (x, y - 1) ) # up
This function does the same thing that the recursive version of floodfill() does, but with a stack instead of recursion. This is possible because recursion is really just using a stack itself (i.e. the call stack). But just as learning how to make programs with functions makes your programs easier to write (and if it was written by someone else, easier to read), once you master recursion, it is a very simple way to write programs that do complex tasks.
You can email Al any questions you have at [email protected]




