“How much math do I need to know to program?” Not That Much, Actually.
Sun 18 March 2012 Al Sweigart
Here are some posts I’ve seen on the r/learnprogramming subreddit forum:
- How much math do you need to become a good programmer?
- Should I brush up on math?
- This may be the dumbest question I have ever posted online. How much math does one actually need to be a good programmer?
Math and programming have a somewhat misunderstood relationship. Many people think that you have to be good at math or made good grades in math class before you can even begin to learn programming. But how much math does a person need to know in order to program?
Not that much actually. This article will go into detail about the kinds of math you should know for programming. You probably know it already.
For general programming, you should know the following:
- Addition, subtraction, division, and multiplication – And really, the computer will be doing the adding, subtracting, dividing, and multiplying for you anyway. You just have to know when you need to do these operations.
- Mod – The mod operation is the “remainder” and its sign is usually the % percent sign. So 23 divided by 7 is 3 with a remainder of 2. But 23 mod 7 is 2.
- The even/odd mod test trick – If you want to know if a number is odd or even, mod it by 2. If the result is 0, the number is even. If the result is 1, the number is odd. 23 mod 2 is 1, so you know 23 is odd. 24 mod 2 is 0, so you know 24 is even. If x mod 2 is 0, you know that whatever number is stored in the variable x is even.
- To get a percentage of a number, multiply that number by the percent number with the decimal point in front of it. So to get 54% of 279, multiple 0.54 * 279. This is why 1.0 often means 100% and 0.0 means 0%.
- Know what negative numbers are. A negative number times a negative number is a positive. A negative times a positive is negative. That’s about it.
- Know what a Cartesian coordinate system is. In programming, the (0, 0) origin is the top left corner of the screen or window, and the Y axis increases going down.
- Know the Pythagorean theorem, and that it can be used to find the distance between two points on a Cartesian coordinate system. The Pythagorean theorem is a^2 + b^2 = c^2. What this usually means in programming is the distance between coordinate (x1, y1) and (x2, y2) will just be sqrt( (x1 – x2)^2 + (y1 – y2)^2 ).
- Know what decimal, binary, and hexadecimal numbering systems are. Decimal numbers are the numbers we’re used to that have ten digits: 0 to 9. It’s commonly thought that humans develop this system because we have ten fingers and counted on our fingers.
Computers work with binary data, which is a number system with only two digits: 0 and 1. This is because we build computers out of electronics components where it’s cheaper to make them only recognize two different states (one state to represent 0 and the other to represent 1).
The numbers are still the exact same, but they are written out differently because there are a different number of digits in each system. Because hex has 6 more digits than the 0-9 numerals can provide, we use the letters A through F for the digits above 9. The easiest way to show these number systems is with an odometer. The following three odometers always show the same number, but they are written out differently in different number systems:
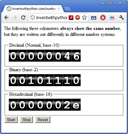
See the Odometer Number Systems page in a new window.
You don’t even have to know the math of converting a number from one number system to another. Every programming language has functions that can do this for you.
(On a side note, hexadecimal is used because one hexadecimal digit can represent exactly four binary digits. So since 3 in hex represents 0011 in binary and A in hex represents 1010. This has the nice effect that the hex number 3A (which is 58 in decimal) is written in binary as 00111010. Hex is used in programming because it is a shorthand for binary. Nobody likes writing out all those ones and zeros.)
And that’s about it. Other than the number system stuff, you probably already knew all the math you needed to know to do programming. Despite the popular conception, math isn’t really used that much in programming. You would need to know math in order to write programs that do, say, earthquake simulators. But that’s more about needing to know math for earthquakes rather than needing to know math for programming an earthquake simulator.
Advanced Mathematics in Some Areas of Programming
There’s a few areas of programming where some additional math knowledge might be needed (but for 95% of the software you’ll write, you don’t need to know it.)
3D games and 3D graphics – 3D stuff will usually involve knowing trigonometry and linear algebra (that is, math dealing with matrices). Of course, there are many 3D graphics libraries that implement all this math programming for you, so you don’t need to know the math.
2D physics (like Angry Birds) and 3D physics (like many popular 3D games use) – To do programming that involves physics, you’ll need to learn some physics equations and formulas (specifically mechanics, which is the type of physics with springs, gravity, and balls rolling down inclined planes.) However, there are several physics engines and software libraries that implement this stuff for you, so you really don’t need to know the physics equations to make a game like Angry Birds.
Cryptography – And really, by cryptography, I just mean RSA. In which case, you’d have to learn some math about how prime numbers work and doing the Greatest Common Divisor (which is a dead simple algorithm, although plenty of programming languages have gcd() function that does this for you.) Other encryption ciphers are mostly moving data around in specific steps. For example, this Flash animation shows the steps in the AES “Rijndael” cipher. All the steps are basically substituting numbers for other numbers, shifting rows of numbers over, mixing up columns of numbers, and doing basic addition with numbers.
And that’s just if you want to write your own encryption ciphers (which you shouldn’t do, because there are already plenty of good ones and without expertise your cipher will probably suck and be easily cracked.) If you just want to write a program that encrypts data, there are software libraries that implement encryption and decryption functions already.
So even for the above situations, you don’t need to know the math to make programs with 3D graphics, physics, or encryption. Just learn to use the libraries.
What You Do Need to Learn to Do Programming
What you do need to learn is how to model data and devise algorithms. This basically means, how to take some real-world calculation or some data processing, and write out code that makes the computer do it. For example, in the game Dungeons and Dragons the characters and monsters have several different statistics for combat:
- HP, or hit points, is the amount of damage a person can take before dying. More HP means you can take more damage before dying.
- AC, or armor class, is a measure of the chance your armor has of blocking an attack. The lower the AC, the more protective the armor is.
- THAC0 (pronounced “thay-co”), or “To Hit Armor Class 0”, is a measure of how skillful the person is at making a successful hit on an opponent. The lower the THAC0, the more accurate the person’s attack is.
- The damage of the weapon is written out as something like 1d6+2. This means the damage is the amount from rolling 1 six-sided dice, and then adding 2 to it. A damage stat of 2d4 would be rolling 2 four-sided dice and adding them together. (Dungeons and Dragons uses 4, 6, 8, 10, 12, and 20-sided dice.)
To see if an attacker hits a defender, the attacker rolls a twenty-sided die. If this number is equal to or greater than the attacker’s THAC0 minus the defender’s AC, then the hit is successful and the defender takes damage. Otherwise, the defender has either dodged or blocked the attack and takes no damage.
Let’s take two Dungeon and Dragons characters, Alice and Bob, with the following stats:
- Alice: HP 14, AC 5, THAC0 18, DAMAGE 1d6
- Bob: HP 12, AC 7, THAC0 16, DAMAGE 2d4
So Alice has two more hit points than Bob and better armor (remember, lower AC is better). But Bob is more likely to make a successful hit (remember, lower THAC0 is better) and does more damage. We can tell Bob’s damage is better because 2d4 will result in 2 to 8 points of damage, while Alice’s 1d6 will result in 1 to 6 points of damage. (If you knew statistics math, you could calculate that Bob’s expected value of damage is 5, which is larger than Alice’s expected value of damage is 3.5.)
So would you bet on Alice or Bob to win in a fight? It’s hard to tell, they seem pretty evenly matched. Even if you knew a lot of statistics, doing all these calculations would be a pain. But you don’t need to know statistics in order to write a program that simulates Dungeons and Dragons combat (that is, models this process) and then run several hundred or thousand simulated fights and see who wins on average.
Here’s such a program written in Python: (Download source)
import random, copy NUM_FIGHTS = 1 VERBOSE = True # Lower thac0 and lower ac values are better. Higher damage & hp values are better. aliceTemplate = {'name': 'Alice', 'hp': 14, 'ac': 5, 'thac0': 18, 'dmgnum': 1, 'dmgsize':6, 'dmgmod': 0} bobTemplate = {'name': 'Bob', 'hp': 12, 'ac': 7, 'thac0': 16, 'dmgnum': 2, 'dmgsize':4, 'dmgmod': 0} def display(s): if VERBOSE: print(s) def attack(attacker, defender): if random.randint(1, 20) >= attacker['thac0'] - defender['ac']: damage = 0 for i in range(attacker['dmgnum']): damage += random.randint(1, attacker['dmgsize']) damage += attacker['dmgmod'] display('%s (%s hp) hits %s (%s hp) for %s points of damage. %s is reduced to %s hp.' % (attacker['name'], attacker['hp'], defender['name'], defender['hp'], damage, defender['name'], defender['hp'] - damage)) defender['hp'] -= damage else: display('%s misses %s.' % (attacker['name'], defender['name'])) aliceWins = 0 bobWins = 0 for i in range(NUM_FIGHTS): display('======================') display('Start of combat #%s' % (i+1)) alice = copy.deepcopy(aliceTemplate) bob = copy.deepcopy(bobTemplate) while True: attack(alice, bob) if bob['hp'] <= 0: break attack(bob, alice) if alice['hp'] <= 0: break if alice['hp'] <= 0: display('Alice has died.') bobWins += 1 if bob['hp'] <= 0: display('Bob has died.') aliceWins += 1 print() print('Alice won %s (%s%%) fights. Bob won %s (%s%%) fights.' % (aliceWins, round(aliceWins / NUM_FIGHTS * 100, 2), bobWins, round(bobWins / NUM_FIGHTS * 100, 2)))
When you run this program, it produces output like this:
====================== Start of combat #1 Alice misses Bob. Bob (12 hp) hits Alice (14 hp) for 6 points of damage. Alice is reduced to 8 hp. Alice misses Bob. Bob misses Alice. Alice misses Bob. Bob misses Alice. Alice misses Bob. Bob misses Alice. Alice (8 hp) hits Bob (12 hp) for 5 points of damage. Bob is reduced to 7 hp. Bob misses Alice. Alice misses Bob. Bob misses Alice. Alice misses Bob. Bob (7 hp) hits Alice (8 hp) for 2 points of damage. Alice is reduced to 6 hp. Alice (6 hp) hits Bob (7 hp) for 6 points of damage. Bob is reduced to 1 hp. Bob misses Alice. Alice (6 hp) hits Bob (1 hp) for 1 points of damage. Bob is reduced to 0 hp. Bob has died. Alice won 1 (100.0%) fights. Bob won 0 (0.0%) fights.
But maybe Alice just got lucky in this one fight. Let’s reprogram this program to turn off the verbose output (displaying text on the screen takes a lot more time than running the simulation) and up the number of fights to 30,000 (this is just changing the NUM_FIGHTS variable to 30000 and the VERBOSE variable to False):
Alice won 12909 (43.03%) fights. Bob won 17091 (56.97%) fights.
So we can see that with the given stats, Bob is at a slight advantage. The computer just ran 30,000 simulated fights. If we were to play 30,000 fights of Dungeons and Dragons with pencil, paper, and physical dice, it would take months to calculate this. But my laptop had the results in less than 8 seconds.
But what if we increased Alice’s hit points from 14 to 20. Who would win then?
Alice won 19438 (64.79%) fights. Bob won 10562 (35.21%) fights.
We see that those 6 extra hit points turns the tables and gives Alice the advantage. How about if her hit points were only increased to 16 instead of 20?
Alice won 15176 (50.59%) fights. Bob won 14824 (49.41%) fights.
We see that just tweaking the stats by 2 hit points is just enough to even out the advantages that Bob gets from his higher level of damage.
And when you look at this program, the only math it uses is addition, subtraction, and multiplication and division to find a percentage. Even if we made the simulation more sophisticated to account for the effects of magic spells, healing potions, multiple attackers, and switching to different weapons in mid-combat, we wouldn’t need to know more math or have made good math grades to do the programming for it.
Sure, go ahead and learn more math. It can only help you become a better programmer. But how much math do you need to know to program? Very little, actually.
UPDATE: I guess I'd add basic algebra to the required knowledge, but only insofar as that if X * 3 = 12 knowing why X is 4.
(Here's a list of other discussions on Reddit about this topic.)
- Math in programming - I'm concerned that I should give up trying (89 comments)
- Is there hope for having a career in programming if I'm terrible at math? (50 comments)
- What areas of math are the most important to computer science/programming? (26 comments)
- Why is Discrete Math so important? (20 comments)
- How much math do you need to become a good programmer? (20 comments)
- Is it possible to be "almost ok" at math and still be a good desirable programmer? (13 comments)
- Should I brush up on math? (10 comments)
- This may be the dumbest question I have ever posted online. How much math does one actually need to be a good programmer? (11 comments)
- I'm trying to learn c++ but why do tutorials always have math problems? (7 comments)
- Worth while improving math skills? (8 comments)
- What math courses should I take if I really want to delve into 3D? (15 comments)
- What is a better supplement to a BS in Computer Science? Math or Physics? (11 comments)
- The importance of Math for Programming? (6 comments)










