|
|
Capítulo 16 |
Simulación de IA para Reversi |
Temas Tratados En Este Capítulo:
· Simulaciones
· Porcentajes
· Gráficos de Torta
· División Entera
· La función round()
· Partidas “Computadora vs. Computadora”
El algoritmo de IA de Reversi es simple, pero consigue vencerme en casi todas las partidas. Esto es porque la computadora puede procesar instrucciones rápido, entonces comprobar todas las posiciones en el tablero y elegir la jugada que da el mayor puntaje es fácil para la computadora. Seguir este procedimiento a mano me tomaría demasiado tiempo.
El programa Reversi del Capítulo 14 tenía dos funciones, obtenerJugadaJugador() y obtenerJugadaComputadora(), las cuales devolvían una jugada en forma de lista [x, y] de dos elementos. Además ambas funciones tenían los mismos parámetros: la estructura de datos tablero y la baldosa correspondiente al jugador. obtenerJugadaJugador() decidía qué jugada [x, y] devolver permitiendo al jugador escribir sus coordenadas. obtenerJugadaComputadora() decidía qué jugada devolver ejecutando el algoritmo de IA de Reversi.
¿Qué pasa cuando reemplazamos la llamada a obtenerJugadaJugador() por una llamada a obtenerJugadaComputadora()? En este caso el jugador nunca ingresaría una jugada, sino que ¡la computadora lo haría por él! ¡La computadora estaría jugando contra sí misma!
Crearemos tres nuevos programas, cada uno basado en el programa Reversi del capítulo anterior:
· Crearemos AISim1.py a partir de reversi.py
· Crearemos AISim2.py a partir de AISim1.py
· Crearemos AISim3.py a partir de AISim2.py
Haciendo que la Computadora Juegue contra sí Misma
Para guardar el archivo reversi.py como AISim1.py haz clic en File (Archivo) ► Save As (Guardar Como), y luego ingresa AISim1.py como nombre de archivo y haz clic en Guardar. Esto creará una copia del código fuente de Reversi en un nuevo archivo que podrás modificar sin que los cambios afecten al juego Reversi original (tal vez quieras volver a jugarlo). Cambia la siguiente línea en AISim1.py:
266. jugada = obtenerJugadaJugador(tableroPrincipal, baldosaJugador)
Por esta otra (el cambio está en negrita):
266. jugada = obtenerJugadaComputadora(tableroPrincipal, baldosaJugador)
Ahora ejecuta el programa. Observa que el juego aún te pregunta si quieres ser X u O, pero no te pedirá que ingreses ninguna jugada. Al haber reemplazado obtenerJugadaJugador(), ya no se llama al código que obtiene esta entrada del jugador. Todavía debes pulsar enter luego de las jugadas que originalmente correspondían a la computadora (debido a la instrucción input('Presiona enter para ver la jugada de la computadora.') en la línea 285), ¡pero la partida se juega sola!
Hagamos algunos otros cambios a AISim1.py. Todas las funciones que has definido para Reversi pueden permanecer iguales. Pero reemplacemos toda la sección principal del programa (de la línea 246 en adelante) por el código que se muestra a continuación. Aunque algo del código permanecerá igual, cambiaremos la mayor parte. Pero las líneas anteriores a 246 son las mismas que en el programa Reversi del capítulo anterior.
Si obtienes errores luego de escribir este código, compara lo que has escrito con el código del libro usando la herramienta diff online en http://invpy.com/es/diff/AISim1.
AISim1.py
246. print('¡Bienvenido a Reversi!')
247.
248. while True:
249. # Reiniciar el tablero y la partida.
250. tableroPrincipal = obtenerNuevoTablero()
251. reiniciarTablero(tableroPrincipal)
252. if quiénComienza() == 'jugador':
253. turno = 'X'
254. else:
255. turno = 'O'
256. print('La ' + turno + ' comenzará.')
257.
258. while True:
259. dibujarTablero(tableroPrincipal)
260. puntajes = obtenerPuntajeTablero(tableroPrincipal)
261. print('X ha obtenido %s puntos. O ha obtenido %s puntos.' % (puntajes['X'], puntajes['O']))
262. input('Presiona Enter para continuar.')
263.
264. if turno == 'X':
265. # Turno de X.
266. otraBaldosa = 'O'
267. x, y = obtenerJugadaComputadora(tableroPrincipal, 'X')
268. hacerJugada(tableroPrincipal, 'X', x, y)
269. else:
270. # Turno de O.
271. otraBaldosa = 'X'
272. x, y = obtenerJugadaComputadora(tableroPrincipal, 'O')
273. hacerJugada(tableroPrincipal, 'O', x, y)
274.
275. if obtenerJugadasVálidas(tableroPrincipal, otraBaldosa) == []:
276. break
277. else:
278. turno = otraBaldosa
279.
280. # Mostrar el puntaje final.
281. dibujarTablero(tableroPrincipal)
282. puntajes = obtenerPuntajeTablero(tableroPrincipal)
283. print('X ha obtenido %s puntos. O ha obtenido %s puntos.' % (puntajes['X'], puntajes['O']))
284.
285. if not jugarDeNuevo():
286. sys.exit()
Cómo Funciona el Código de AISim1.py
El programa AISim1.py es prácticamente igual programa original Reversi, excepto que la llamada a obtenerJugadaJugador() ha sido reemplazada por una llamada a obtenerJugadaComputadora(). Ha habido también otros cambios menores al texto que se imprime en la pantalla para hacer que la partida sea más fácil de seguir.
Cuando ejecutas el programa AISim1.py, todo lo que puedes hacer es pulsar enter luego de cada turno hasta que la partida termine. Prueba ejecutar algunas partidas y observa a la computadora jugar contra sí misma. Ambos jugadores X y O usan el mismo algoritmo, de modo que es realmente cuestión de suerte quién gana. Cada jugador ganará aproximadamente la mitad de las veces.
Haciendo que la Computadora Juegue contra sí Misma Varias Veces
Pero ¿qué pasaría si creásemos un nuevo algoritmo? Entonces podríamos hacer jugar esta nueva IA contra la que hemos implementado en obtenerJugadaComputadora(), y ver cuál es mejor. Hagamos algunos cambios al código fuente. Haz lo siguiente para crear AISim2.py:
1. Haz clic en File (Archivo) ► Save As (Guardar Como).
2. Guarda este archivo como AISim2.py de modo que puedas hacer cambios sin afectar a AISim1.py. (En este punto, AISim1.py y AISim2.py tendrán el mismo código.)
3. Haz cambios a AISim2.py y guarda ese archivo. (AISim2.py contendrá los nuevos cambios y AISim1.py mantendrá el código original, sin modificar.)
Añade el siguiente código. Los agregados están en negrita, y algunas líneas han sido eliminadas. Cuando hayas terminado de hacer cambios en el archivo, guárdalo como AISim2.py.
AISim2.py
Si obtienes errores luego de copiar este código, compáralo con el código del libro usando la herramienta diff online en http://invpy.com/es/diff/AISim2.
AISim2.py
246. print('¡Bienvenido a Reversi!')
247.
248. victoriasx = 0
249. victoriaso = 0
250. empates = 0
251. numPartidas = int(input('Ingresa el número de partidas a jugar: '))
252.
253. for partida in range(numPartidas):
254. print('Partida #%s:' % (partida), end=' ')
255. # Reiniciar el tablero y la partida.
256. tableroPrincipal = obtenerNuevoTablero()
257. reiniciarTablero(tableroPrincipal)
258. if quiénComienza() == 'jugador':
259. turno = 'X'
260. else:
261. turno = 'O'
262.
263. while True:
264. if turno == 'X':
265. # Turno de X.
266. otraBaldosa = 'O'
267. x, y = obtenerJugadaComputadora(tableroPrincipal, 'X')
268. hacerJugada(tableroPrincipal, 'X', x, y)
269. else:
270. # Turno de O.
271. otraBaldosa = 'X'
272. x, y = obtenerJugadaComputadora(tableroPrincipal, 'O')
273. hacerJugada(tableroPrincipal, 'O', x, y)
274.
275. if obtenerJugadasVálidas(tableroPrincipal, otraBaldosa) == []:
276. break
277. else:
278. turno = otraBaldosa
279.
280. # Mostrar el puntaje final.
281. puntajes = obtenerPuntajeTablero(tableroPrincipal)
282. print('X ha obtenido %s puntos. O ha obtenido %s puntos.' % (puntajes['X'], puntajes['O']))
283.
284. if puntajes['X'] > puntajes['O']:
285. victoriasx += 1
286. elif puntajes['X'] < puntajes['O']:
287. victoriaso += 1
288. else:
289. empates += 1
290.
291. numPartidas = float(numPartidas)
292. porcentajex = round(((victoriasx / numPartidas) * 100), 2)
293. porcentajeo = round(((victoriaso / numPartidas) * 100), 2)
294. porcentajeempate = round(((empates / numPartidas) * 100), 2)
295. print('X ha ganado %s partidas (%s%%), O ha ganado %s partidas (%s%%), empates en %s partidas (%s%%) sobre un total de %s partidas.' % (victoriasx, porcentajex, victoriaso, porcentajeo, empates, porcentajeempate, numPartidas))
Cómo Funciona el Código de AISim2.py
Hemos agregado las variables victoriasx, victoriaso y empates en las líneas 248 a 250 para llevar un registro de cuántas veces gana X, cuántas gana O y cuántas veces se produce un empate. Las líneas 284 a 289 incrementan estas variables al final de cada partida, antes de que el bucle se reinicie con un nuevo juego.
Hemos eliminado del programa la mayoría de las llamadas a la función print(), así como las llamadas a dibujarTablero(). Cuando ejecutes AISim2.py, te preguntará cuántas partidas deseas simular. Ahora que hemos quitado la llamada a dibujarTablero() y reemplazado el bucle while True el bucle for partida in range(numPartidas):, el programa puede simular un número de partidas sin detenerse a esperar que el usuario escriba nada. Aquí hay una prueba de ejecución de diez partidas computadora vs. computadora de Reversi:
¡Bienvenido a Reversi!
Ingresa el número de partidas a jugar: 10
Partida #0: X ha obtenido 40 puntos. O ha obtenido 23 puntos.
Partida #1: X ha obtenido 24 puntos. O ha obtenido 39 puntos.
Partida #2: X ha obtenido 31 puntos. O ha obtenido 30 puntos.
Partida #3: X ha obtenido 41 puntos. O ha obtenido 23 puntos.
Partida #4: X ha obtenido 30 puntos. O ha obtenido 34 puntos.
Partida #5: X ha obtenido 37 puntos. O ha obtenido 27 puntos.
Partida #6: X ha obtenido 29 puntos. O ha obtenido 33 puntos.
Partida #7: X ha obtenido 31 puntos. O ha obtenido 33 puntos.
Partida #8: X ha obtenido 32 puntos. O ha obtenido 32 puntos.
Partida #9: X ha obtenido 41 puntos. O ha obtenido 22 puntos.
X ha ganado 5 partidas (50.0%), O ha ganado 4 partidas (40.0%), empates en 1 partidas (10.0%) sobre un total de 10.0 partidas.
Como los algoritmos tienen una componente aleatoria, puede ser que no obtengas exactamente los mismos números.
Imprimir cosas en la pantalla enlentece a la computadora, pero ahora que hemos eliminado ese código, la computadora puede jugar una partida completa de Reversi en uno o dos segundos. Piensa en esto. Cada vez que el programa imprime una de esas líneas con el puntaje final significa que ha jugado una partida completa (que son alrededor de cincuenta o sesenta jugadas, cada una de las cuales ha sido cuidadosamente comprobada para verificar que da la mayor cantidad posible de puntos).
Porcentajes
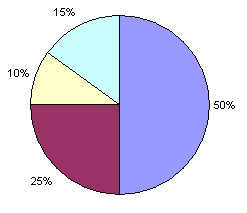
Figura 16-1: Un gráfico de torta con porciones de 10%, 15%, 25% y 50%.
Los porcentajes son una porción de una cantidad total, y están comprendidos entre 0% y 100%. Si tienes el 100% de una torta, quiere decir que tienes toda la torta. Si tienes el 0% de una torta, significa que no tienes torta en absoluto. 50% de la torta corresponde a la mitad de la torta. Una torta es una imagen de uso común cuando hablamos de porcentajes. De hecho, hay un tipo de gráfico llamado gráfico de torta que muestra a qué fracción del total corresponde una dada porción. La Figura 16-1 muestra un gráfico de torta dividido en porciones de 10%, 15%, 25% y 50%. Nota que la suma de 10% + 15% + 25% + 50% da un total de 100%: una torta entera.
Podemos calcular el porcentaje a través de una división. Para obtener un porcentaje, divide la parte que tienes por el total, y multiplica ese resultado por cien. Por ejemplo, si X ha ganado 50 partidas de 100, puedes calcular la expresión 50 / 100, que da como resultado 0.5. Multiplica este resultado por 100 para obtener un porcentaje (en este caso, 50%).
Observa que si X hubiese ganado 100 partidas de 200, podrías calcular el porcentaje dividiendo 100 / 200, que también se evaluaría a 0.5. Al multiplicar 0.5 por 100 para obtener el porcentaje, volverías a obtener 50%. Ganar 100 partidas de 200 es el mismo porcentaje (es decir, la misma porción) que ganar 50 juegos de 100.
La División se Evalúa a Punto Flotante
Es importante destacar que cuando al usar el operador / división, la expresión siempre se evaluará a un número de punto flotante. Por ejemplo, la expresión 10 / 2 se evaluará al valor de punto flotante 5.0, no al valor entero 5.
Es importante recordar esto, porque sumar un entero a un valor de punto flotante con el operador + suma también se evaluará siempre a un valor de punto flotante. Por ejemplo, 3 + 4.0 se evaluará al valor de punto flotante 7.0 y no al entero 7.
Prueba ingresar el siguiente código en la consola interactiva:
>>> spam = 100 / 4
>>> spam
25.0
>>> spam = spam + 20
>>> spam
45.0
Observa que en el ejemplo de arriba, el tipo de datos del valor almacenado en spam es siempre un valor de punto flotante. Puedes pasar el valor de punto flotante a la función int(), la cuál devolverá una forma entera del valor de punto flotante. Pero esto siempre redondeará el valor de punto flotante hacia abajo. Por ejemplo, las expresiones int(4.0), int(4.2) e int(4.9) se evaluarán a 4, y nunca a 5.
La función round()
La función round() redondeará un número float al float entero más cercano. Prueba ingresar lo siguiente en la consola interactiva:
>>> round(10.0)
10.0
>>> round(10.2)
10.0
>>> round(8.7)
9.0
>>> round(3.4999)
3.0
>>> round(2.5422, 2)
2.54
La función round() también tiene un parámetro opcional, donde puedes especificar hasta qué lugar quieres redondear el número. Por ejemplo, la expresión round(2.5422, 2) se evalúa a 2.54 y round(2.5422, 3) se evalúa a 2.542.
Mostrando las Estadísticas
291. numPartidas = float(numPartidas)
292. porcentajex = round(((victoriasx / numPartidas) * 100), 2)
293. porcentajeo = round(((victoriaso / numPartidas) * 100), 2)
294. porcentajeempate = round(((empates / numPartidas) * 100), 2)
295. print('X ha ganado %s partidas (%s%%), O ha ganado %s partidas (%s%%), empates en %s partidas (%s%%) sobre un total de %s partidas.' % (victoriasx, porcentajex, victoriaso, porcentajeo, empates, porcentajeempate, numPartidas))
El código al final del programa muestra al usuario cuántas veces han ganado X y O, cuántas veces han empatado, y a qué porcentajes corresponden estos números. Estadísticamente, cuantas más partidas simules, más exactos serán tus resultados para indicar cuál es el mejor algoritmo IA. Si sólo simulas diez partidas y X gana 3 de ellas, parecerá que el algoritmo de X gana sólo el 30% de las veces. Sin embargo, si simulases cien, o incluso mil partidas, probablemente veas que el algoritmo de X gana cerca del 50% (es decir, la mitad) de las partidas.
Para hallar los porcentajes, divide el número de victorias o empates por el número total de partidas. Luego, multiplica el resultado por 100. Aquí es posible que llegues a un número como 66.66666666666667. Entonces pasa este número a la función round() utilizando 2 como segundo parámetro para limitar la precisión a dos lugares decimales, de modo que devuelva en su lugar un float como 66.67 (el cual es mucho más legible).
Probemos otro experimento. Ejecuta AISim2.py de nuevo, pero esta vez hazlo simular 100 juegos:
Prueba de Ejecución de AISim2.py
¡Bienvenido a Reversi!
Ingresa el número de partidas a jugar: 100
Partida #0: X ha obtenido 42 puntos. O ha obtenido 18 puntos.
Partida #1: X ha obtenido 26 puntos. O ha obtenido 37 puntos.
Partida #2: X ha obtenido 34 puntos. O ha obtenido 29 puntos.
Partida #3: X ha obtenido 40 puntos. O ha obtenido 24 puntos.
...omitido por brevedad...
Partida #96: X ha obtenido 22 puntos. O ha obtenido 39 puntos.
Partida #97: X ha obtenido 38 puntos. O ha obtenido 26 puntos.
Partida #98: X ha obtenido 35 puntos. O ha obtenido 28 puntos.
Partida #99: X ha obtenido 24 puntos. O ha obtenido 40 puntos.
X ha ganado 46 partidas (46.0%), O ha ganado 52 partidas (52.0%), empates en 2 partidas (2.0%) sobre un total de 100.0 partidas.
Dependiendo de qué tan rápida sea tu computadora, esto puede llegar a tomar un par de minutos. Puedes ver que los resultados de los cien juegos tienden a ser mitad y mitad, ya que tanto X como O están usando el mismo algoritmo.
Comparando Diferentes Algoritmos IA
Vamos a agregar algunas nuevas funciones con algoritmos nuevos. Pero primero hagamos clic en File (Archivo) ► Save As (Guardar Como), y guardemos este archivo como AISim3.py. Agrega las siguientes funciones antes de la línea print('¡Bienvenido a Reversi!').
AISim3.py
Si obtienes errores luego de escribir este código, compáralo con el código fuente del libro usando la herramienta diff online en http://invpy.com/es/diff/AISim3.
AISim3.py
245. def obtenerJugadaAleatoria(tablero, baldosa):
246. # Devuelve una jugada al azar.
247. return random.choice(obtenerJugadasVálidas(tablero, baldosa))
248.
249.
250. def esBorde(x, y):
251. return x == 0 or x == 7 or y == 0 or y == 7
252.
253.
254. def obtenerEsquinaBordeMejorJugada(tablero, baldosa):
255. # Devuelve una jugada sobre una esquina, lado o la mejor jugada.
256. jugadasPosibles = obtenerJugadasVálidas(tablero, baldosa)
257.
258. # Ordena al azar las jugadas posibles.
259. random.shuffle(jugadasPosibles)
260.
261. # Ordena al azar las jugadas posibles.
262. for x, y in jugadasPosibles:
263. if esEsquina(x, y):
264. return [x, y]
265.
266. # Siempre ir por una esquina de ser posible.
267. for x, y in jugadasPosibles:
268. if esBorde(x, y):
269. return [x, y]
270.
271. return obtenerJugadaComputadora(tablero, baldosa)
272.
273.
274. def obtenerBordeMejorJugada(tablero, baldosa):
275. # Devuelve una jugada a una esquina, un lado o la mejor jugada posible.
276. jugadasPosibles = obtenerJugadasVálidas(tablero, baldosa)
277.
278. # Ordena al azar las jugadas posibles.
279. random.shuffle(jugadasPosibles)
280.
281. # Devuelve una jugada sobre un borde de ser posible.
282. for x, y in jugadasPosibles:
283. if esBorde(x, y):
284. return [x, y]
285.
286. return obtenerJugadaComputadora(tablero, baldosa)
287.
288.
289. def obtenerPeorJugada(tablero, baldosa):
290. # Devuelve la jugada que que convierta la menor cantidad de baldosas.
291. jugadasPosibles = obtenerJugadasVálidas(tablero, baldosa)
292.
293. # Ordena al azar las jugadas posibles.
294. random.shuffle(jugadasPosibles)
295.
296. # Recorre todas las jugadas posibles y recuerda la de mejor puntaje.
297. peorPuntaje = 64
298. for x, y in jugadasPosibles:
299. réplicaTablero = obtenerCopiaTablero(tablero)
300. hacerJugada(réplicaTablero, baldosa, x, y)
301. puntaje = obtenerPuntajeTablero(réplicaTablero)[baldosa]
302. if puntaje < peorPuntaje:
303. peorJugada = [x, y]
304. peorPuntaje = score
305.
306. return peorJugada
307.
308.
309. def obtenerEsquinaPeorJugada(tablero, baldosa):
310. # Devuelve la esquina, el especio o la jugada que convierta la menor cantidad de baldosas.
311. jugadasPosibles = obtenerJugadasVálidas(tablero, baldosa)
312.
313. # randomize the order of the possible moves
314. random.shuffle(possibleMoves)
315.
316. # Ordena al azar las jugadas posibles.
317. for x, y in jugadasPosibles:
318. if esEsquina(x, y):
319. return [x, y]
320.
321. return obtenerPeorJugada(tablero, baldosa)
322.
323.
324.
325. print('¡Bienvenido a Reversi!')
Cómo Funciona el Código de AISim3.py
Muchas de estas funciones son similares entre sí, y algunas de ellas usan la nueva función esBorde(). Aquí hay un recuento de los nuevos algoritmos que hemos creado:
Tabla 17-1: Funciones usadas para nuestra IA Reversi.
|
Function |
Description |
|
obtenerJugadaAleatoria() |
Elige al azar una jugada válida. |
|
obtenerEsquinaBordeMejorJugada() |
Juega en una esquina si hay alguna disponible. Si no hay esquinas, juega sobre un borde. Si no hay bordes disponibles, usa el algoritmo obtenerJugadaComputadora(). |
|
obtenerBordeMejorJugada() |
Toma un espacio sobre un borde si hay alguno disponible. Si no los hay, usa el algoritmo obtenerJugadaComputadora(). Esto quiere decir que se prefiere jugar sobre un borde antes que sobre una esquina. |
|
obtenerPeorJugada() |
Elige el espacio que resulta en la menor cantidad de baldosas convertidas. |
|
obtenerEsquinaPeorJugada() |
Juega sobre una esquina, si hay alguna disponible. Si no hay ninguna, usa el algoritmo obtenerPeorJugada(). |
Comparando el Algoritmo Aleatorio contra el Algoritmo Regular
Ahora lo único que queda por hacer es reemplazar una de las llamadas a obtenerJugadaComputadora() en la parte principal del programa por una de las nuevas funciones. Luego puedes simular varias partidas y ver con qué frecuencia un algoritmo vence al otro. Primero, reemplacemos el algoritmo de O por obtenerJugadaAleatoria() en la línea 351:
351. x, y = obtenerJugadaAleatoria(tableroPrincipal, 'O')
Ahora cuando ejecutes el programa con cien juegos, se verá aproximadamente así:
¡Bienvenido a Reversi!
Ingresa el número de partidas a jugar: 100
Partida #0: X ha obtenido 25 puntos. O ha obtenido 38 puntos.
Partida #1: X ha obtenido 32 puntos. O ha obtenido 32 puntos.
Partida #2: X ha obtenido 15 puntos. O ha obtenido 0 puntos.
...omitido por brevedad...
Partida #97: X ha obtenido 41 puntos. O ha obtenido 23 puntos.
Partida #98: X ha obtenido 33 puntos. O ha obtenido 31 puntos.
Partida #99: X ha obtenido 45 puntos. O ha obtenido 19 puntos.
X ha ganado 84 partidas (84.0%), O ha ganado 15 partidas (15.0%), empates en 1 partidas (1.0%) sobre un total de 100.0 partidas.
¡Vaya! X ha ganado muchas más partidas que O. Esto quiere decir que el algoritmo de obtenerJugadaComputadora() (jugar sobre las esquinas disponibles, o de otro modo tomar la jugada que convierta la mayor cantidad de baldosas) ha ganado más partidas que el algoritmo de obtenerJugadaAleatoria() (que elige jugadas al azar). Esto tiene sentido, ya que hacer elecciones inteligentes suele ser mejor que simplemente jugar al azar.
Comparando el Algoritmo Aleatorio contra sí Mismo
¿Y qué pasaría si cambiásemos el algoritmo de X para que también usase obtenerJugadaAleatoria()? Averigüémoslo cambiando obtenerJugadaComputadora() por obtenerJugadaAleatoria() en la llamada a la función de X en la línea 346 y ejecutando el programa otra vez.
¡Bienvenido a Reversi!
Ingresa el número de partidas a jugar: 100
Partida #0: X ha obtenido 37 puntos. O ha obtenido 24 puntos.
Partida #1: X ha obtenido 19 puntos. O ha obtenido 45 puntos.
...omitido por brevedad...
Partida #98: X ha obtenido 27 puntos. O ha obtenido 37 puntos.
Partida #99: X ha obtenido 38 puntos. O ha obtenido 22 puntos.
X ha ganado 42 partidas (42.0%), O ha ganado 54 partidas (54.0%), empates en 4 partidas (4.0%) sobre un total de 100.0 partidas.
Como puedes ver, cuando ambos jugadores juegan al azar cada uno gana aproximadamente el 50% de las veces. (En el caso de arriba, O parece haber tenido suerte ya que ganó algo más que la mitad de las partidas.)
Así como jugar en las esquinas es una buena idea porque estas fichas no pueden ser reconvertidas, jugar sobre los bordes también puede ser una buena idea. Sobre los lados, una baldosa tiene el borde del tablero y no está tan expuesta como las otras fichas. Las esquinas siguen siendo preferibles a los bordes, pero jugar sobre los lados (incluso cuando haya una movida que puede convertir más fichas) puede ser una buena estrategia.
Comparando el Algoritmo Regular contra el Algoritmo EsquinaBordeMejor
Cambiemos el algoritmo de X en la línea 346 por la función obtenerJugadaComputadora() (el algoritmo original) y el algoritmo de O en la línea 351 por obtenerEsquinaBordeMejorJugada() (que primero intenta jugar en una esquina, luego sobre un lado y finalmente toma la mejor jugada restante), y simulemos cien juegos para ver cuál es mejor. Prueba cambiar las llamadas a las funciones y ejecutar el programa de nuevo.
¡Bienvenido a Reversi!
Ingresa el número de partidas a jugar: 100
Partida #0: X ha obtenido 52 puntos. O ha obtenido 12 puntos.
Partida #1: X ha obtenido 10 puntos. O ha obtenido 54 puntos.
...omitido por brevedad...
Partida #98: X ha obtenido 41 puntos. O ha obtenido 23 puntos.
Partida #99: X ha obtenido 46 puntos. O ha obtenido 13 puntos.
X ha ganado 65 partidas (65.0%), O ha ganado 31 partidas (31.0%), empates en 4 partidas (4.0%) sobre un total de 100.0 partidas.
¡Vaya! Eso fue inesperado. Parece que elegir una jugada sobre el borde antes que una jugada que convierte más baldosas es una mala estrategia. El beneficio de jugar sobre el borde es menor que el costo de convertir menos baldosas del oponente. ¿Podemos confiar en estos resultados? Ejecutemos el programa de nuevo, pero juguemos mil partidas esta vez. Es posible que esto tome algunos minutos en tu computadora (¡pero tomaría semanas si quisieras hacerlo a mano!) Intenta cambiar las llamadas a las funciones y ejecutar de nuevo el programa.
¡Bienvenido a Reversi!
Ingresa el número de partidas a jugar: 1000
Partida #0: X ha obtenido 20 puntos. O ha obtenido 44 puntos.
Partida #1: X ha obtenido 54 puntos. O ha obtenido 9 puntos.
...omitido por brevedad...
Partida #998: X ha obtenido 38 puntos. O ha obtenido 23 puntos.
Partida #999: X ha obtenido 38 puntos. O ha obtenido 26 puntos.
X ha ganado 611 partidas (61.1%), O ha ganado 363 partidas (36.3%), empates en 26 partidas (2.6%) sobre un total de 1000.0 partidas.
La estadística de mayor precisión correspondiente a una ejecución de mil partidas es aproximadamente la misma que la estadística de la ejecución de cien partidas. Parece ser que elegir una jugada que convierte más baldosas es mejor idea que jugar sobre un borde.
Comparando el Algoritmo Regular contra el Algoritmo Peor
Ahora usemos obtenerJugadaComputadora() en la línea 346 para el algoritmo del jugador X y obtenerPeorJugada() en la línea 351 para el algoritmo del jugador O (este último elige la jugada que convierte la menor cantidad de fichas), y simulemos cien partidas. Prueba cambiar las llamadas a las funciones y ejecutar el programa de nuevo.
¡Bienvenido a Reversi!
Ingresa el número de partidas a jugar: 100
Partida #0: X ha obtenido 50 puntos. O ha obtenido 14 puntos.
Partida #1: X ha obtenido 38 puntos. O ha obtenido 8 puntos.
...omitido por brevedad...
Partida #98: X ha obtenido 36 puntos. O ha obtenido 16 puntos.
Partida #99: X ha obtenido 19 puntos. O ha obtenido 0 puntos.
X ha ganado 98 partidas (98.0%), O ha ganado 2 partidas (2.0%), empates en 0 partidas (0.0%) sobre un total de 100.0 partidas.
¡Vaya! El algoritmo en obtenerPeorJugada(), que siempre elige la jugada que convierte el menor número de baldosas, perderá casi siempre contra el algoritmo regular. Esto realmente no es sorprendente. (De hecho, ¡es sorprendente que esta estrategia haya conseguido ganar incluso un 2% de las partidas!)
Comparando el Algoritmo Regular contra el Algoritmo EsquinaPeor
¿Qué tal si reemplazamos obtener obtenerPeorJugada() en la línea 351 por obtenerEsquinaPeorJugada()? Este es el mismo algoritmo, excepto que toma cualquier posición disponible sobre una esquina antes de elegir la peor jugada. Prueba cambiar la llamada a la función y ejecutar de nuevo el programa.
¡Bienvenido a Reversi!
Ingresa el número de partidas a jugar: 100
Partida #0: X ha obtenido 36 puntos. O ha obtenido 7 puntos.
Partida #1: X ha obtenido 44 puntos. O ha obtenido 19 puntos.
...omitido por brevedad...
Partida #98: X ha obtenido 47 puntos. O ha obtenido 17 puntos.
Partida #99: X ha obtenido 36 puntos. O ha obtenido 18 puntos.
X ha ganado 94 partidas (94.0%), O ha ganado 6 partidas (6.0%), empates en 0 partidas (0.0%) sobre un total de 100.0 partidas.
El algoritmo obtenerEsquinaPeorJugada() aún pierde la mayoría de las partidas, pero parece ganar algunas más que obtenerPeorJugada() (6% comparado con un 2% del anterior). ¿Hace realmente una diferencia el jugar sobre las esquinas cuando están disponibles?
Comparando el Algoritmo Peor contra el Algoritmo EsquinaPeor
Podemos comprobar esto asignando obtenerPeorJugada() al algoritmo de X y obtenerEsquinaPeorJugada() al algoritmo de O, y luego ejecutando el programa. Prueba cambiar las llamadas a las funciones y ejecutar de nuevo el programa.
¡Bienvenido a Reversi!
Ingresa el número de partidas a jugar: 100
Partida #0: X ha obtenido 25 puntos. O ha obtenido 39 puntos.
Partida #1: X ha obtenido 26 puntos. O ha obtenido 33 puntos.
...omitido por brevedad...
Partida #98: X ha obtenido 36 puntos. O ha obtenido 25 puntos.
Partida #99: X ha obtenido 29 puntos. O ha obtenido 35 puntos.
X ha ganado 32 partidas (32.0%), O ha ganado 67 partidas (67.0%), empates en 1 partidas (1.0%) sobre un total de 100.0 partidas.
Efectivamente, incluso cuando en el resto de los casos estamos tomando la peor jugada, parece ser que jugar sobre las esquinas resulta en un mayor número de victorias. A pesar de que hemos comprobado que jugar sobre un borde hace que pierdas más frecuentemente, jugar sobre las esquinas siempre es una buena idea.
Resumen
Este capítulo no se ha tratado realmente de ningún juego nuevo, sino que ha presentado el modelado de varias estrategias para Reversi. Si quisiésemos comprobar a mano la efectividad de una estrategia tendríamos que pasar semanas, incluso meses, ejecutando cuidadosamente partidas de Reversi a mano y anotando los resultados. Pero si sabemos cómo programar una computadora para jugar Reversi, entonces podemos hacer que simule partidas por nosotros utilizando estas estrategias. Si piensas en esto, ¡verás que la computadora ejecuta millones de líneas de nuestro programa de Python en segundos! Tus experimentos con la simulación de Reversi pueden incluso ayudarte a mejorar tu estrategia para jugar Reversi en la vida real.
De hecho, este capítulo podría ser un buen proyecto para una feria de ciencias. El problema aquí es averiguar qué conjunto de jugadas consigue el mayor número de victorias contra otros conjuntos de jugadas, y elaborar una hipótesis sobre cuál es la mejor estrategia. Después de ejecutar varias simulaciones, puedes determinar qué estrategia funciona mejor. ¡Usando programación puedes convertir en un proyecto de feria de ciencias la simulación de cualquier juego de mesa! Y todo gracias a que sabes cómo dar instrucciones a la computadora para hacerlo, paso por paso, línea por línea. Puedes hablar el idioma de la computadora, y conseguir que haga por tí una enorme cantidad de procesamiento de datos y cálculo de números.
Eso ha sido lo último que veremos en este libro sobre juegos basados en texto. Los juegos que sólo utilizan texto pueden ser divertidos, incluso a pesar de ser simples. Pero la mayoría de los juegos modernos usan gráficos, sonido y animación para crear juegos con mucho más atractivo visual. En el resto de los capítulos de este libro, aprenderemos a crear juegos con gráficos usando un módulo de Python llamado Pygame.
