







Use this link to get 70% off the Automate the Boring Stuff online video course.
Support me on Patreon









This chapter goes over some simple mathematical concepts you will use in the rest of this book. In two-dimensional (2D) games, the graphics on the screen can move left or right and up or down. These games need a way to translate a place on the screen into integers the program can deal with.
This is where the Cartesian coordinate system comes in. Coordinates are numbers that represent a specific point on the screen. These numbers can be stored as integers in your program’s variables.
A common way to refer to specific places on a chessboard is by marking each row and column with letters and numbers. Figure 12-1 shows a chessboard that has each row and column marked.
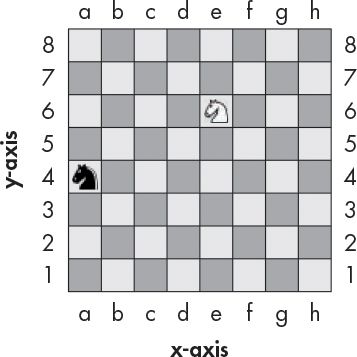
Figure 12-1: A sample chessboard with a black knight at (a, 4) and a white knight at (e, 6)
A coordinate for a space on the chessboard is a combination of a row and a column. In chess, the knight piece looks like a horse head. The white knight in Figure 12-1 is located at the point (e, 6) since it is in column e and row 6, and the black knight is located at point (a, 4) because it is in column a and row 4.
You can think of a chessboard as a Cartesian coordinate system. By using a row label and column label, you can give a coordinate that is for one—and only one—space on the board. If you’ve learned about Cartesian coordinate systems in math class, you may know that numbers are used for both the rows and columns. A chessboard using numerical coordinates would look like Figure 12-2.
The numbers going left and right along the columns are part of the x-axis. The numbers going up and down along the rows are part of the y-axis. Coordinates are always described with the x-coordinate first, followed by the y-coordinate. In Figure 12-2, the x-coordinate for the white knight is 5 and the y-coordinate is 6, so the white knight is located at the coordinates (5, 6) and not (6, 5). Similarly, the black knight is located at the coordinate (1, 4), not (4, 1), since the black knight’s x-coordinate is 1 and its y-coordinate is 4.
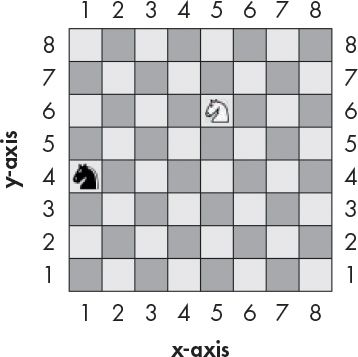
Figure 12-2: The same chessboard but with numeric coordinates for both rows and columns
Notice that for the black knight to move to the white knight’s position, the black knight must move two spaces up and four spaces to the right. But you don’t need to look at the board to figure this out. If you know the white knight is located at (5, 6) and the black knight is located at (1, 4), you can use subtraction to figure out this information.
Subtract the black knight’s x-coordinate from the white knight’s x-coordinate: 5 – 1 = 4. The black knight has to move along the x-axis by four spaces. Now subtract the black knight’s y-coordinate from the white knight’s y-coordinate: 6 – 4 = 2. The black knight has to move along the y-axis by two spaces.
By doing some math with the coordinate numbers, you can figure out the distances between two coordinates.
Cartesian coordinates also use negative numbers—numbers that are less than zero. A minus sign in front of a number shows it is negative: –1 is less than 0. And –2 is less than –1. But 0 itself isn’t positive or negative. In Figure 12-3, you can see the positive numbers increasing to the right and the negative numbers decreasing to the left on a number line.

Figure 12-3: A number line with positive and negative numbers
The number line is useful to see subtraction and addition. You can think of the expression 5 + 3 as the white knight starting at position 5 and moving 3 spaces to the right. As you can see in Figure 12-4, the white knight ends up at position 8. This makes sense, because 5 + 3 is 8.
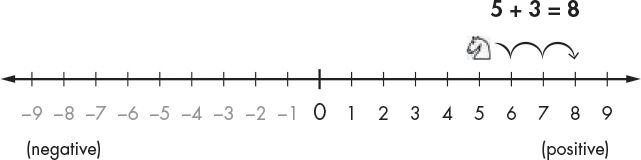
Figure 12-4: Moving the white knight to the right adds to the coordinate.
You subtract by moving the white knight to the left. So if the expression is 5 – 6, the white knight starts at position 5 and moves 6 spaces to the left, as shown in Figure 12-5.
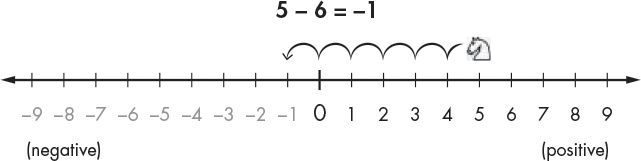
Figure 12-5: Moving the white knight to the left subtracts from the coordinate.
The white knight ends up at position –1. That means 5 – 6 equals –1.
If you add or subtract a negative number, the white knight moves in the opposite direction than it does with positive numbers. If you add a negative number, the knight moves to the left. If you subtract a negative number, the knight moves to the right. The expression –1 – (–4) would be equal to 3, as shown in Figure 12-6. Notice that –1 – (–4) has the same answer as –1 + 4.

Figure 12-6: The knight starts at –6 and moves to the right by 4 spaces.
You can think of the x-axis as a number line. Add another number line going up and down for the y-axis. If you put these two number lines together, you have a Cartesian coordinate system like the one in Figure 12-7.
Adding a positive number (or subtracting a negative number) would move the knight up on the y-axis or to the right on the x-axis, and subtracting a positive number (or adding a negative number) would move the knight down on the y-axis or to the left on the x-axis.
The (0, 0) coordinate at the center is called the origin. You may have used a coordinate system like this in your math class. As you’re about to see, coordinate systems like these have a lot of little tricks you can use to make figuring out coordinates easier.
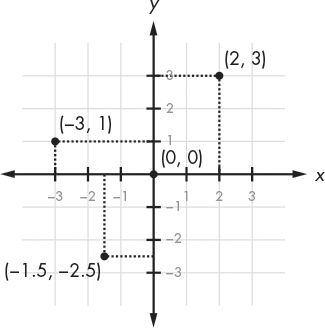
Figure 12-7: Putting two number lines together creates a Cartesian coordinate system.
Your computer screen is made up of pixels, the smallest dot of color a screen can show. It’s common for computer screens to use a coordinate system that has the origin (0, 0) at the top-left corner and that increases going down and to the right. You can see this in Figure 12-8, which shows a laptop with a screen resolution that is 1,920 pixels wide and 1,080 pixels tall.
There are no negative coordinates. Most computer graphics use this coordinate system for pixels on the screen, and you will use it in this book’s games. For programming, it’s important to know how coordinate systems work—both the kind used for mathematics and the kind used for computer screens.
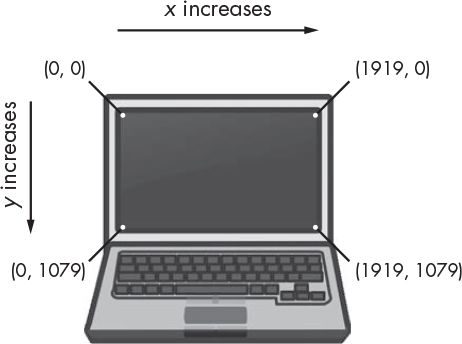
Figure 12-8: The Cartesian coordinate system on a computer screen
Subtracting and adding negative numbers is easy when you have a number line in front of you. It can also be easy without a number line. Here are three tricks to help you add and subtract negative numbers by yourself.
When you see a minus sign with a plus sign on the left, you can replace the plus sign with a minus sign. Imagine the minus sign “eating” the plus sign to its left. The answer is still the same, because adding a negative value is the same as subtracting a positive value. So 4 + –2 and 4 – 2 both evaluate to 2, as you can see here:
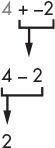
When you see the two minus signs next to each other without a number between them, they can combine into a plus sign. The answer is still the same, because subtracting a negative value is the same as adding a positive value:
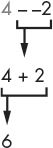
You can always swap the numbers in addition. This is the commutative property of addition. That means that doing a swap like 6 + 4 to 4 + 6 will not change the answer, as you can see when you count the boxes in Figure 12-9.
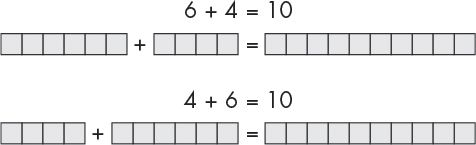
Figure 12-9: The commutative property of addition lets you swap numbers.
Say you are adding a negative number and a positive number, like –6 + 8. Because you are adding numbers, you can swap the order of the numbers without changing the answer. This means –6 + 8 is the same as 8 + –6. Then when you look at 8 + –6, you see that the minus sign can eat the plus sign to its left, and the problem becomes 8 – 6 = 2, as you can see here:

You’ve rearranged the problem so that it’s easier to solve without using a calculator or computer.
A number’s absolute value is the number without the minus sign in front of it. Therefore, positive numbers do not change, but negative numbers become positive. For example, the absolute value of –4 is 4. The absolute value of –7 is 7. The absolute value of 5 (which is already positive) is just 5.
You can figure out the distance between two objects by subtracting their positions and taking the absolute value of the difference. Imagine that the white knight is at position 4 and the black knight is at position –2. The distance would be 6, since 4 – –2 is 6, and the absolute value of 6 is 6.
It works no matter what the order of the numbers is. For example, –2 – 4 (that is, negative two minus four) is –6, and the absolute value of –6 is also 6.
Python’s abs() function returns the absolute value of an integer. Enter the following into the interactive shell:
>>> abs(-5)
5
>>> abs(42)
42
>>> abs(-10.5)
10.5
The absolute value of -5 is 5. The absolute value of a positive number is just the number, so the absolute value of 42 is 42. Even numbers with decimals have an absolute value, so the absolute value of -10.5 is 10.5.
Most programming doesn’t require understanding a lot of math. Up until this chapter, we’ve been getting by with simple addition and multiplication.
Cartesian coordinate systems are needed to describe where a certain position is located in a two-dimensional area. Coordinates have two numbers: the x-coordinate and the y-coordinate. The x-axis runs left and right, and the y-axis runs up and down. On a computer screen, the origin is in the top-left corner and the coordinates increase going right and downward.
The three math tricks you learned in this chapter make it easy to add positive and negative integers. The first trick is that a minus sign will eat the plus sign on its left. The second trick is that two minuses next to each other will combine into a plus sign. The third trick is that you can swap the position of the numbers you are adding.
The rest of the games in this book use these concepts because they have two-dimensional areas in them. All graphical games require understanding how Cartesian coordinates work.