14
CAESAR CIPHER

The program in this chapter isn’t really a game, but it is fun nevertheless. The program will convert normal English into a secret code. It can also convert secret codes back into regular English. Only someone who knows the key to the secret codes will be able to understand the messages.

Because this program manipulates text to convert it into secret messages, you’ll learn several new functions and methods for manipulating strings. You’ll also learn how programs can do math with text strings just as they can with numbers.

Cryptography and Encryption

The science of writing secret codes is called cryptography. For thousands of years, cryptography has made it possible to send secret messages that only the sender and recipient could read, even if someone captured the messenger and read the coded message. A secret code system is called a cipher. The cipher used by the program in this chapter is called the Caesar cipher.

In cryptography, we call the message that we want to keep secret the plaintext. Let’s say we have a plaintext message that looks like this:

There is a clue behind the bookshelf.

Converting the plaintext into the encoded message is called encrypting the plaintext. The plaintext is encrypted into the ciphertext. The ciphertext looks like random letters, so we can’t understand what the original plaintext was just by looking at the ciphertext. Here is the previous example encrypted into ciphertext:

aolyl pz h jsBl ilopuk Aol ivvrzolsm.

If you know the cipher used to encrypt the message, you can decrypt the ciphertext back to the plaintext. (Decryption is the opposite of encryption.)

Many ciphers use keys, which are secret values that let you decrypt ciphertext that was encrypted with a specific cipher. Think of the cipher as being like a door lock. You can only unlock it with a particular key.

If you’re interested in writing cryptography programs, you can read my book Hacking Secret Ciphers with Python. It’s free to download from http://inventwithpython.com/hacking/.

How the Caesar Cipher Works

The Caesar cipher was one of the earliest ciphers ever invented. In this cipher, you encrypt a message by replacing each letter in it with a “shifted” letter. In cryptography, the encrypted letters are called symbols because they can be letters, numbers, or any other signs. If you shift the letter A by one space, you get the letter B. If you shift the letter A by two spaces, you get the letter C. Figure 14-1 shows some letters shifted by three spaces.

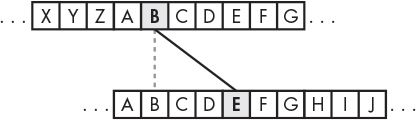
Figure 14-1: A Caesar cipher shifting letters by three spaces. Here, B becomes E.

To get each shifted letter, draw a row of boxes with each letter of the alphabet. Then draw a second row of boxes under it, but start your letters a certain number of spaces over. When you get to the end of the plaintext alphabet, wrap back around to A. Figure 14-2 shows an example with the letters shifted by three spaces.

Figure 14-2: The entire alphabet shifted by three spaces

The number of spaces you shift your letters (between 1 and 26) is the key in the Caesar cipher. Unless you know the key (the number used to encrypt the message), you won’t be able to decrypt the secret code. The example in Figure 14-2 shows the letter translations for the key 3.

If you encrypt the plaintext word HOWDY with a key of 3, then:

• The letter H becomes K.

• The letter O becomes R.

• The letter W becomes Z.

• The letter D becomes G.

• The letter Y becomes B.

So, the ciphertext of HOWDY with the key 3 becomes KRZGB. To decrypt KRZGB with the key 3, we go from the bottom boxes back to the top.

If you would like to include lowercase letters as distinct from uppercase letters, then add another 26 boxes to the ones you already have and fill them with the 26 lowercase letters. Now with a key of 3, the letter Y becomes b, as shown in Figure 14-3.

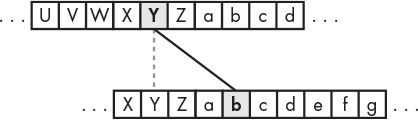
Figure 14-3: The entire alphabet, now including lowercase letters, shifted by three spaces

The cipher works the same way as it did with just uppercase letters. In fact, if you want to use letters from another language’s alphabet, you can write boxes with those letters to create your cipher.

Sample Run of Caesar Cipher

Here is a sample run of the Caesar Cipher program encrypting a message:

Do you wish to encrypt or decrypt a message?
encrypt
Enter your message:
The sky above the port was the color of television, tuned to a dead channel.
Enter the key number (1-52)
13
Your translated text is:
gur FxL noBIr Gur CBEG JnF Gur pByBE Bs GryrIvFvBA, GHArq GB n qrnq punAAry.

Now run the program and decrypt the text that you just encrypted:

Do you wish to encrypt or decrypt a message?
decrypt
Enter your message:
gur FxL noBIr Gur CBEG JnF Gur pByBE Bs GryrIvFvBA, GHArq GB n qrnq punAAry.
Enter the key number (1-52)
13
Your translated text is:
The sky above the port was the color of television, tuned to a dead channel.

If you do not decrypt with the correct key, the text will not decrypt properly:

Do you wish to encrypt or decrypt a message?
decrypt
Enter your message:
gur FxL noBIr Gur CBEG JnF Gur pByBE Bs GryrIvFvBA, GHArq GB n qrnq punAAry.
Enter the key number (1-52)
15
Your translated text is:
Rfc qiw YZmtc rfc nmpr uYq rfc amjmp md rcjctgqgml, rslcb rm Y bcYb afYllcj.

Source Code for Caesar Cipher

Enter this source code for the Caesar Cipher program and then save the file as cipher.py.

If you get errors after entering this code, compare the code you typed to the book’s code with the online diff tool at https://www.nostarch.com/inventwithpython#diff.

cipher.py

 1. # Caesar Cipher
 2. SYMBOLS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz'
 3. MAX_KEY_SIZE = len(SYMBOLS)
 4.
 5. def getMode():
 6.     while True:
 7.         print('Do you wish to encrypt or decrypt a message?')
 8.         mode = input().lower()
 9.         if mode in ['encrypt', 'e', 'decrypt', 'd']:
10.             return mode
11.         else:
12.             print('Enter either "encrypt" or "e" or "decrypt" or "d".')
13.
14. def getMessage():
15.     print('Enter your message:')
16.     return input()
17.
18. def getKey():
19.     key = 0
20.     while True:
21.         print('Enter the key number (1-%s)' % (MAX_KEY_SIZE))
22.         key = int(input())
23.         if (key >= 1 and key <= MAX_KEY_SIZE):
24.             return key
25.
26. def getTranslatedMessage(mode, message, key):
27.     if mode[0] == 'd':
28.         key = -key
29.     translated = ''
30.
31.     for symbol in message:
32.         symbolIndex = SYMBOLS.find(symbol)
33.         if symbolIndex == -1: # Symbol not found in SYMBOLS.
34.             # Just add this symbol without any change.
35.             translated += symbol
36.         else:
37.             # Encrypt or decrypt.
38.             symbolIndex += key
39.
40.             if symbolIndex >= len(SYMBOLS):
41.                 symbolIndex -= len(SYMBOLS)
42.             elif symbolIndex < 0:
43.                 symbolIndex += len(SYMBOLS)
44.
45.             translated += SYMBOLS[symbolIndex]
46.     return translated
47.
48. mode = getMode()
49. message = getMessage()
50. key = getKey()
51. print('Your translated text is:')
52. print(getTranslatedMessage(mode, message, key))

Setting the Maximum Key Length

The encryption and decryption processes are the reverse of each other, but they share much of the same code. Let’s look at how each line works:

1. # Caesar Cipher
2. SYMBOLS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz'
3. MAX_KEY_SIZE = len(SYMBOLS)

MAX_KEY_SIZE is a constant that stores the length of SYMBOLS (52). This constant reminds us that in this program, the key used in the cipher should always be between 1 and 52.

Deciding to Encrypt or Decrypt the Message

The getMode() function lets the user decide whether they want to use the program’s encryption or decryption mode:

 5. def getMode():
 6.     while True:
 7.         print('Do you wish to encrypt or decrypt a message?')
 8.         mode = input().lower()
 9.         if mode in ['encrypt', 'e', 'decrypt', 'd']:
10.             return mode
11.         else:
12.             print('Enter either "encrypt" or "e" or "decrypt" or "d".')

Line 8 calls input() to let the user enter the mode they want. The lower() method is then called on this string to return a lowercase version of the string. The value returned from input().lower() is stored in mode. The if statement’s condition checks whether the string stored in mode exists in the ['encrypt', 'e', 'decrypt', 'd'] list.

This function will return the string in mode as long as mode is equal to 'encrypt', 'e', 'decrypt', or 'd'. Therefore, getMode() will return the string mode. If the user types something that is not 'encrypt', 'e', 'decrypt', or 'd', then the while loop will ask them again.

Getting the Message from the Player

The getMessage() function simply gets the message to encrypt or decrypt from the user and returns it:

14. def getMessage():
15.     print('Enter your message:')
16.     return input()

The call for input() is combined with return so that we use only one line instead of two.

Getting the Key from the Player

The getKey() function lets the player enter the key they will use to encrypt or decrypt the message:

18. def getKey():
19.     key = 0
20.     while True:
21.         print('Enter the key number (1-%s)' % (MAX_KEY_SIZE))
22.         key = int(input())
23.         if (key >= 1 and key <= MAX_KEY_SIZE):
24.             return key

The while loop ensures that the function keeps looping until the user enters a valid key. A valid key here is one between the integer values 1 and 52 (remember that MAX_KEY_SIZE is 52 because there are 52 characters in the SYMBOLS variable). The getKey() function then returns this key. Line 22 sets key to the integer version of what the user entered, so getKey() returns an integer.

Encrypting or Decrypting the Message

The getTranslatedMessage() function does the actual encrypting and decrypting:

26. def getTranslatedMessage(mode, message, key):
27.     if mode[0] == 'd':
28.         key = -key
29.     translated = ''

It has three parameters:

mode This sets the function to encryption mode or decryption mode.

message This is the plaintext (or ciphertext) to be encrypted (or decrypted).

key This is the key that is used in this cipher.

Line 27 checks whether the first letter in the mode variable is the string 'd'. If so, then the program is in decryption mode. The only difference between decryption and encryption mode is that in decryption mode, the key is set to the negative version of itself. For example, if key is the integer 22, then decryption mode sets it to -22. The reason is explained in “Encrypting or Decrypting Each Letter” on page 205.

The translated variable will contain the string of the result: either the ciphertext (if you are encrypting) or the plaintext (if you are decrypting). It starts as a blank string and has encrypted or decrypted characters concatenated to the end of it. Before we can start concatenating the characters to translated, however, we need to encrypt or decrypt the text, which we’ll do in the rest of getTranslatedMessage().

Finding Passed Strings with the find() String Method

In order to shift the letters around to do the encryption or decryption, we first need to convert them into numbers. The number for each letter in the SYMBOLS string will be the index where it appears. Since the letter A is at SYMBOLS[0], the number 0 will represent the capital A. If we wanted to encrypt this with the key 3, we would simply use 0 + 3 to get the index of the encrypted letter: SYMBOLS[3] or 'D'.

We’ll use the find() string method, which finds the first occurrence of a passed string in the string on which the method is called. Enter the following in the interactive shell:

>>> 'Hello world!'.find('H')
0
>>> 'Hello world!'.find('o')
4
>>> 'Hello world!'.find('ell')
1

'Hello world!'.find('H') returns 0 because the 'H' is found at the first index of the string 'Hello world!'. Remember, indexes start at 0, not 1. The code 'Hello world!'.find('o') returns 4 because the lowercase 'o' is first found at the end of 'Hello'. The find() method stops looking after the first occurrence, so the second 'o' in 'world' doesn’t matter. You can also find strings with more than one character. The string 'ell' is found starting at index 1.

If the passed string cannot be found, the find() method returns -1:

>>> 'Hello world!'.find('xyz')
-1

Let’s go back to the Caesar Cipher program. Line 31 is a for loop that iterates on each character in the message string:

31.     for symbol in message:
32.         symbolIndex = SYMBOLS.find(symbol)
33.         if symbolIndex == -1: # Symbol not found in SYMBOLS.
34.             # Just add this symbol without any change.
35.             translated += symbol

The find() method is used on line 32 to get the index of the string in symbol. If find() returns -1, the character in symbol will just be added to translated without any change. This means that any characters that aren’t part of the alphabet, such as commas and periods, won’t be changed.

Encrypting or Decrypting Each Letter

Once you’ve found a letter’s index number, adding the key to the number will perform the shift and give you the index for the encrypted letter.

Line 38 does this addition to get the encrypted (or decrypted) letter.

37.             # Encrypt or decrypt.
38.             symbolIndex += key

Remember that on line 28, we made the integer in key negative for decryption. The code that adds the key will now subtract it, since adding a negative number is the same as subtraction.

However, if this addition (or subtraction, if key is negative) causes symbolIndex to go past the last index of SYMBOLS, we’ll need to wrap around to the beginning of the list at 0. This is handled by the if statement starting at line 40:

40.             if symbolIndex >= len(SYMBOLS):
41.                 symbolIndex -= len(SYMBOLS)
42.             elif symbolIndex < 0:
43.                 symbolIndex += len(SYMBOLS)
44.
45.             translated += SYMBOLS[symbolIndex]

Line 40 checks whether symbolIndex has gone past the last index by comparing it to the length of the SYMBOLS string. If it has, line 41 subtracts the length of SYMBOLS from symbolIndex. If symbolIndex is now negative, then the index needs to wrap around to the other side of the SYMBOLS string. Line 42 checks whether the value of symbolIndex is negative after adding the decryption key. If so, line 43 adds the length of SYMBOLS to symbolIndex.

The symbolIndex variable now contains the index of the correctly encrypted or decrypted symbol. SYMBOLS[symbolIndex] will point to the character for this index, and this character is added to the end of translated on line 45.

The execution loops back to line 31 to repeat this for the next character in message. Once the loop is done, the function returns the encrypted (or decrypted) string in translated on line 46:

46.     return translated

The last line in the getTranslatedMessage() function returns the translated string.

Starting the Program

The start of the program calls each of the three functions defined previously to get the mode, message, and key from the user:

48. mode = getMode()
49. message = getMessage()
50. key = getKey()
51. print('Your translated text is:')
52. print(getTranslatedMessage(mode, message, key))

These three values are passed to getTranslatedMessage(), whose return value (the translated string) is printed to the user.

The Brute-Force Technique

That’s the entire Caesar cipher. However, while this cipher may fool some people who don’t understand cryptography, it won’t keep a message secret from someone who knows cryptanalysis. While cryptography is the science of making codes, cryptanalysis is the science of breaking codes.

The whole point of cryptography is to make sure that if someone else gets their hands on the encrypted message, they cannot figure out the original text. Let’s pretend we are the code breaker and all we have is this encrypted text:

LwCjBA uiG vwB jm xtmiAivB, jCB kmzBiqvBG qA ijACzl.

Brute-forcing is the technique of trying every possible key until you find the correct one. Because there are only 52 possible keys, it would be easy for a cryptanalyst to write a hacking program that decrypts with every possible key. Then they could look for the key that decrypts to plain English. Let’s add a brute-force feature to the program.

Adding the Brute-Force Mode

First, change lines 7, 9, and 12—which are in the getMode() function—to look like the following (the changes are in bold):

 5. def getMode():
 6.     while True:
 7.         print('Do you wish to encrypt or decrypt or brute-force a
              message?')
 8.         mode = input().lower()
 9.         if mode in ['encrypt', 'e', 'decrypt', 'd', 'brute', 'b']:
10.             return mode
11.         else:
12.             print('Enter either "encrypt" or "e" or "decrypt" or "d" or
                  "brute" or "b".')

This code will let the user select brute force as a mode.

Next, make the following changes to the main part of the program:

48. mode = getMode()
49. message = getMessage()
50. if mode[0] != 'b':
51.     key = getKey()
52. print('Your translated text is:')
53. if mode[0] != 'b':
54.     print(getTranslatedMessage(mode, message, key))
55. else:
56.     for key in range(1, MAX_KEY_SIZE + 1):
57.         print(key, getTranslatedMessage('decrypt', message, key))

If the user is not in brute-force mode, they are asked for a key, the original getTranslatedMessage() call is made, and the translated string is printed.

However, if the user is in brute-force mode, then the getTranslatedMessage() loop iterates from 1 all the way up to MAX_KEY_SIZE (which is 52). Remember that the range() function returns a list of integers up to, but not including, the second parameter, which is why we add + 1. The program will then print every possible translation of the message (including the key number used in the translation). Here is a sample run of this modified program:

Do you wish to encrypt or decrypt or brute-force a message?
brute
Enter your message:
LwCjBA uiG vwB jm xtmiAivB, jCB kmzBiqvBG qA ijACzl.
Your translated text is:
1 KvBiAz thF uvA il wslhzhuA, iBA jlyAhpuAF pz hizByk.
2 JuAhzy sgE tuz hk vrkgygtz, hAz ikxzgotzE oy ghyAxj.
3 Itzgyx rfD sty gj uqjfxfsy, gzy hjwyfnsyD nx fgxzwi.
4 Hsyfxw qeC rsx fi tpiewerx, fyx givxemrxC mw efwyvh.
5 Grxewv pdB qrw eh sohdvdqw, exw fhuwdlqwB lv devxug.
6 Fqwdvu ocA pqv dg rngcucpv, dwv egtvckpvA ku cduwtf.
7 Epvcut nbz opu cf qmfbtbou, cvu dfsubjouz jt bctvse.
8 Doubts may not be pleasant, but certainty is absurd.
9 Cntasr lZx mns ad okdZrZms, ats bdqsZhmsx hr Zartqc.
10 BmsZrq kYw lmr Zc njcYqYlr, Zsr acprYglrw gq YZqspb.
11 AlrYqp jXv klq Yb mibXpXkq, Yrq ZboqXfkqv fp XYproa.
12 zkqXpo iWu jkp Xa lhaWoWjp, Xqp YanpWejpu eo WXoqnZ.
--snip--

After looking over each row, you can see that the eighth message isn’t nonsense but plain English! The cryptanalyst can deduce that the original key for this encrypted text must have been 8. This brute-force method would have been difficult to do back in the days of Julius Caesar and the Roman Empire, but today we have computers that can quickly go through millions or even billions of keys in a short time.

Summary

Computers are good at doing math. When we create a system to translate some piece of information into numbers (as we do with text and ordinals or with space and coordinate systems), computer programs can process these numbers quickly and efficiently. A large part of writing a program is figuring out how to represent the information you want to manipulate as values that Python can understand.

While our Caesar Cipher program can encrypt messages that will keep them secret from people who have to figure them out with pencil and paper, the program won’t keep them secret from people who know how to get computers to process information. (Our brute-force mode proves this.)

In Chapter 15, we’ll create Reversegam (also known as Reversi or Othello). The AI that plays this game is much more advanced than the AI that played Tic-Tac-Toe in Chapter 10. In fact, it’s so good that most of the time you won’t be able to beat it!