








This project features an animation of a 3D cube rotating using trigonometric functions. You can adapt the 3D point rotation math and the line() function in your own animation programs.
Although the block text characters we’ll use to draw the cube don’t look like thin, straight lines, this kind of drawing is called a wireframe model because it renders only the edges of an object’s surfaces. Figure 62-1 shows the wireframe model for a cube and an icosphere, a rough sphere made of triangles.
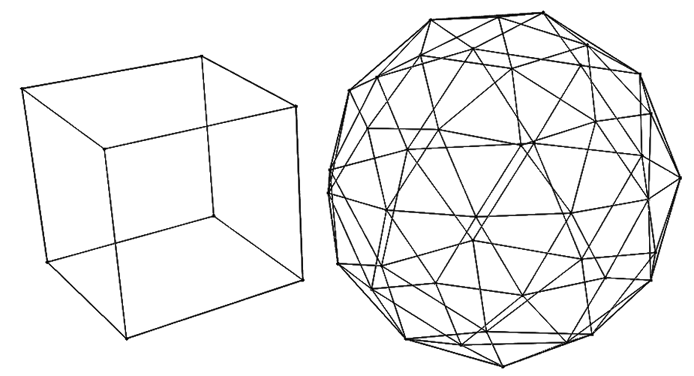
Figure 62-1: The wireframe models for a cube (left) and an icosphere (right)
Figure 62-2 shows what the output will look like when you run rotatingcube.py.

Figure 62-2: The wireframe cube that the program draws to the screen
This algorithm has two main parts: the line() function and the rotatePoint() function. The cube has eight points, one for each corner. The program stores these corners as (x, y, z) tuples in the CUBE_CORNERS list. These points also define the connections for the cube’s edge lines. When all the points rotate in the same direction by the same amount, they give the illusion of a cube rotating.
1. """Rotating Cube, by Al Sweigart [email protected]
2. A rotating cube animation. Press Ctrl-C to stop.
3. View this code at https://nostarch.com/big-book-small-python-projects
4. Tags: large, artistic, math"""
5.
6. # This program MUST be run in a Terminal/Command Prompt window.
7.
8. import math, time, sys, os
9.
10. # Set up the constants:
11. PAUSE_AMOUNT = 0.1 # Pause length of one-tenth of a second.
12. WIDTH, HEIGHT = 80, 24
13. SCALEX = (WIDTH - 4) // 8
14. SCALEY = (HEIGHT - 4) // 8
15. # Text cells are twice as tall as they are wide, so set scaley:
16. SCALEY *= 2
17. TRANSLATEX = (WIDTH - 4) // 2
18. TRANSLATEY = (HEIGHT - 4) // 2
19.
20. # (!) Try changing this to '#' or '*' or some other character:
21. LINE_CHAR = chr(9608) # Character 9608 is '█'
22.
23. # (!) Try setting two of these values to zero to rotate the cube only
24. # along a single axis:
25. X_ROTATE_SPEED = 0.03
26. Y_ROTATE_SPEED = 0.08
27. Z_ROTATE_SPEED = 0.13
28.
29. # This program stores XYZ coordinates in lists, with the X coordinate
30. # at index 0, Y at 1, and Z at 2. These constants make our code more
31. # readable when accessing the coordinates in these lists.
32. X = 0
33. Y = 1
34. Z = 2
35.
36.
37. def line(x1, y1, x2, y2):
38. """Returns a list of points in a line between the given points.
39.
40. Uses the Bresenham line algorithm. More info at:
41. https://en.wikipedia.org/wiki/Bresenham%27s_line_algorithm"""
42. points = [] # Contains the points of the line.
43. # "Steep" means the slope of the line is greater than 45 degrees or
44. # less than -45 degrees:
45.
46. # Check for the special case where the start and end points are
47. # certain neighbors, which this function doesn't handle correctly,
48. # and return a hard coded list instead:
49. if (x1 == x2 and y1 == y2 + 1) or (y1 == y2 and x1 == x2 + 1):
50. return [(x1, y1), (x2, y2)]
51.
52. isSteep = abs(y2 - y1) > abs(x2 - x1)
53. if isSteep:
54. # This algorithm only handles non-steep lines, so let's change
55. # the slope to non-steep and change it back later.
56. x1, y1 = y1, x1 # Swap x1 and y1
57. x2, y2 = y2, x2 # Swap x2 and y2
58. isReversed = x1 > x2 # True if the line goes right-to-left.
59.
60. if isReversed: # Get the points on the line going right-to-left.
61. x1, x2 = x2, x1 # Swap x1 and x2
62. y1, y2 = y2, y1 # Swap y1 and y2
63.
64. deltax = x2 - x1
65. deltay = abs(y2 - y1)
66. extray = int(deltax / 2)
67. currenty = y2
68. if y1 < y2:
69. ydirection = 1
70. else:
71. ydirection = -1
72. # Calculate the y for every x in this line:
73. for currentx in range(x2, x1 - 1, -1):
74. if isSteep:
75. points.append((currenty, currentx))
76. else:
77. points.append((currentx, currenty))
78. extray -= deltay
79. if extray <= 0: # Only change y once extray <= 0.
80. currenty -= ydirection
81. extray += deltax
82. else: # Get the points on the line going left to right.
83. deltax = x2 - x1
84. deltay = abs(y2 - y1)
85. extray = int(deltax / 2)
86. currenty = y1
87. if y1 < y2:
88. ydirection = 1
89. else:
90. ydirection = -1
91. # Calculate the y for every x in this line:
92. for currentx in range(x1, x2 + 1):
93. if isSteep:
94. points.append((currenty, currentx))
95. else:
96. points.append((currentx, currenty))
97. extray -= deltay
98. if extray < 0: # Only change y once extray < 0.
99. currenty += ydirection
100. extray += deltax
101. return points
102.
103.
104. def rotatePoint(x, y, z, ax, ay, az):
105. """Returns an (x, y, z) tuple of the x, y, z arguments rotated.
106.
107. The rotation happens around the 0, 0, 0 origin by angles
108. ax, ay, az (in radians).
109. Directions of each axis:
110. -y
111. |
112. +-- +x
113. /
114. +z
115. """
116.
117. # Rotate around x axis:
118. rotatedX = x
119. rotatedY = (y * math.cos(ax)) - (z * math.sin(ax))
120. rotatedZ = (y * math.sin(ax)) + (z * math.cos(ax))
121. x, y, z = rotatedX, rotatedY, rotatedZ
122.
123. # Rotate around y axis:
124. rotatedX = (z * math.sin(ay)) + (x * math.cos(ay))
125. rotatedY = y
126. rotatedZ = (z * math.cos(ay)) - (x * math.sin(ay))
127. x, y, z = rotatedX, rotatedY, rotatedZ
128.
129. # Rotate around z axis:
130. rotatedX = (x * math.cos(az)) - (y * math.sin(az))
131. rotatedY = (x * math.sin(az)) + (y * math.cos(az))
132. rotatedZ = z
133.
134. return (rotatedX, rotatedY, rotatedZ)
135.
136.
137. def adjustPoint(point):
138. """Adjusts the 3D XYZ point to a 2D XY point fit for displaying on
139. the screen. This resizes this 2D point by a scale of SCALEX and
140. SCALEY, then moves the point by TRANSLATEX and TRANSLATEY."""
141. return (int(point[X] * SCALEX + TRANSLATEX),
142. int(point[Y] * SCALEY + TRANSLATEY))
143.
144.
145. """CUBE_CORNERS stores the XYZ coordinates of the corners of a cube.
146. The indexes for each corner in CUBE_CORNERS are marked in this diagram:
147. 0---1
148. /| /|
149. 2---3 |
150. | 4-|-5
151. |/ |/
152. 6---7"""
153. CUBE_CORNERS = [[-1, -1, -1], # Point 0
154. [ 1, -1, -1], # Point 1
155. [-1, -1, 1], # Point 2
156. [ 1, -1, 1], # Point 3
157. [-1, 1, -1], # Point 4
158. [ 1, 1, -1], # Point 5
159. [-1, 1, 1], # Point 6
160. [ 1, 1, 1]] # Point 7
161. # rotatedCorners stores the XYZ coordinates from CUBE_CORNERS after
162. # they've been rotated by rx, ry, and rz amounts:
163. rotatedCorners = [None, None, None, None, None, None, None, None]
164. # Rotation amounts for each axis:
165. xRotation = 0.0
166. yRotation = 0.0
167. zRotation = 0.0
168.
169. try:
170. while True: # Main program loop.
171. # Rotate the cube along different axes by different amounts:
172. xRotation += X_ROTATE_SPEED
173. yRotation += Y_ROTATE_SPEED
174. zRotation += Z_ROTATE_SPEED
175. for i in range(len(CUBE_CORNERS)):
176. x = CUBE_CORNERS[i][X]
177. y = CUBE_CORNERS[i][Y]
178. z = CUBE_CORNERS[i][Z]
179. rotatedCorners[i] = rotatePoint(x, y, z, xRotation,
180. yRotation, zRotation)
181.
182. # Get the points of the cube lines:
183. cubePoints = []
184. for fromCornerIndex, toCornerIndex in ((0, 1), (1, 3), (3, 2),
(2, 0), (0, 4), (1, 5), (2, 6), (3, 7), (4, 5), (5, 7), (7, 6),
(6, 4)):
185. fromX, fromY = adjustPoint(rotatedCorners[fromCornerIndex])
186. toX, toY = adjustPoint(rotatedCorners[toCornerIndex])
187. pointsOnLine = line(fromX, fromY, toX, toY)
188. cubePoints.extend(pointsOnLine)
189.
190. # Get rid of duplicate points:
191. cubePoints = tuple(frozenset(cubePoints))
192.
193. # Display the cube on the screen:
194. for y in range(HEIGHT):
195. for x in range(WIDTH):
196. if (x, y) in cubePoints:
197. # Display full block:
198. print(LINE_CHAR, end='', flush=False)
199. else:
200. # Display empty space:
201. print(' ', end='', flush=False)
202. print(flush=False)
203. print('Press Ctrl-C to quit.', end='', flush=True)
204.
205. time.sleep(PAUSE_AMOUNT) # Pause for a bit.
206.
207. # Clear the screen:
208. if sys.platform == 'win32':
209. os.system('cls') # Windows uses the cls command.
210. else:
211. os.system('clear') # macOS and Linux use the clear command.
212.
213. except KeyboardInterrupt:
214. print('Rotating Cube, by Al Sweigart [email protected]')
215. sys.exit() # When Ctrl-C is pressed, end the program.After entering the source code and running it a few times, try making experimental changes to it. The comments marked with (!) have suggestions for small changes you can make. On your own, you can also try to figure out how to do the following:
CUBE_CORNERS and the tuple on line 184 to create different wireframe models such as a pyramid and a flat hexagon.CUBE_CORNERS by 1.5 so that the cube revolves around the center of the screen, rather than rotating around its own center.Try to find the answers to the following questions. Experiment with some modifications to the code and rerun the program to see what effect the changes have.
<((0, 1), (1, 3), (3, 2), (2, 0), (0,4), (4, 5), (5, 1))>?