







Use this link to get 70% off the Automate the Boring Stuff online video course.
Support me on Patreon








“People have been defending their own privacy for centuries with whispers, darkness, envelopes, closed doors, secret handshakes, and couriers. The technologies of the past did not allow for strong privacy, but electronic technologies do.”
—Eric Hughes, “A Cypherpunk’s Manifesto” (1993)

In this chapter, you’ll learn about the multiplicative cipher and the affine cipher. The multiplicative cipher is similar to the Caesar cipher but encrypts using multiplication rather than addition. The affine cipher combines the multiplicative cipher and the Caesar cipher, resulting in a stronger and more reliable encryption.
But first, you’ll learn about modular arithmetic and greatest common divisors—two mathematical concepts that are required to understand and implement the affine cipher. Using these concepts, we’ll create a module to handle wraparound and find valid keys for the affine cipher. We’ll use this module when we create a program for the affine cipher in Chapter 14.
Modular arithmetic, or clock arithmetic, refers to math in which numbers wrap around when they reach a particular value. We’ll use modular arithmetic to handle wraparound in the affine cipher. Let’s see how it works.

Figure 13-1: 3 o’clock + 5 hours = 8 o’clock
Imagine a clock with just an hour hand and the 12 replaced with a 0. (If programmers designed clocks, the first hour would begin at 0.) If the current time is 3 o’clock, what time will it be in 5 hours? This is easy enough to figure out: 3 + 5 = 8. It will be 8 o’clock in 5 hours. Think of the hour hand starting at 3 and then moving 5 hours clockwise, as shown in Figure 13-1.
If the current time is 10 o’clock, what time will it be in 5 hours? Adding 5 + 10 = 15, but 15 o’clock doesn’t make sense for clocks that show only 12 hours. To find out what time it will be, you subtract 15 – 12 = 3, so it will be 3 o’clock. (Normally, you would distinguish between 3 am and 3 pm, but that doesn’t matter in modular arithmetic.)
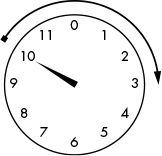
Figure 13-2: 10 o’clock + 5 hours = 3 o’clock
Double-check this math by moving the hour hand clockwise 5 hours, starting from 10. It does indeed land on 3, as shown in Figure 13-2.
If the current time is 10 o’clock, what time will it be in 200 hours? Adding 200 + 10 = 210, and 210 is certainly larger than 12. Because one full rotation brings the hour hand back to its original position, we can solve this problem by subtracting by 12 (which is one full rotation) until the result is a number less than 12. Subtracting 210 – 12 = 198. But 198 is still larger than 12, so we continue to subtract 12 until the difference is less than 12; in this case the final answer will be 6. If the current time is 10 o’clock, the time 200 hours later will be 6 o’clock, as shown in Figure 13-3.
If you want to double-check the 10 o’clock + 200 hours math, you can repeatedly move the hour hand around the clock face. When you move the hour hand for the 200th hour, it should land on 6.
However, it’s easier to have the computer do this modular arithmetic for us with the modulo operator.
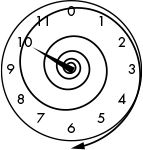
Figure 13-3: 10 o’clock + 200 hours = 6 o’clock
You can use the modulo operator, abbreviated as mod, to write modular expressions. In Python, the mod operator is the percent sign (%). You can think of the mod operator as a kind of division remainder operator; for example, 21 ÷ 5 = 4 with a remainder of 1, and 21 % 5 = 1. Similarly, 15 % 12 is equal to 3, just as 15 o’clock would be 3 o’clock. Enter the following into the interactive shell to see the mod operator in action:
>>> 21 % 5
1
>>> (10 + 200) % 12
6
>>> 10 % 10
0
>>> 20 % 10
0
Just as 10 o’clock plus 200 hours will wrap around to 6 o’clock on a clock with 12 hours, (10 + 200) % 12 will evaluate to 6. Notice that numbers that divide evenly will mod to 0, such as 10 % 10 or 20 % 10.
Later, we’ll use the mod operator to handle wraparound in the affine cipher. It’s also used in the algorithm that we’ll use to find the greatest common divisor of two numbers, which will enable us to find valid keys for the affine cipher.
Factors are the numbers that are multiplied to produce a particular number. Consider 4 × 6 = 24. In this equation, 4 and 6 are factors of 24. Because a number’s factors can also be used to divide that number without leaving a remainder, factors are also called divisors.
The number 24 also has some other factors:
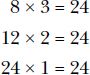
So the factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24.
Let’s look at the factors of 30:
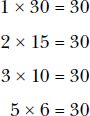
The factors of 30 are 1, 2, 3, 5, 6, 10, 15, and 30. Note that any number will always have 1 and itself as its factors because 1 times a number is equal to that number. Notice too that the list of factors for 24 and 30 have 1, 2, 3, and 6 in common. The greatest of these common factors is 6, so 6 is the greatest common factor, more commonly known as the greatest common divisor (GCD), of 24 and 30.
It’s easiest to find a GCD of two numbers by visualizing their factors. We’ll visualize factors and the GCD using Cuisenaire rods. A Cuisenaire rod is made up of squares equal to the number the rod represents, and the rods help us visualize math operations. Figure 13-4 uses Cuisenaire rods to visualize 3 + 2 = 5 and 5 × 3 = 15.
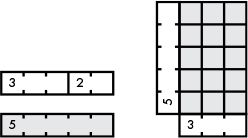
Figure 13-4: Using Cuisenaire rods to demonstrate addition and multiplication
A rod of 3 added to a rod of 2 is the same length as a rod of 5. You can even use rods to find answers to multiplication problems by making a rectangle with sides made from rods of the numbers you want to multiply. The number of squares in the rectangle is the answer to the multiplication problem.
If a rod 20 units long represents the number 20, a number is a factor of 20 if that number’s rods can evenly fit inside the 20-square rod. Figure 13-5 shows that 4 and 10 are factors of 20 because they fit evenly into 20.
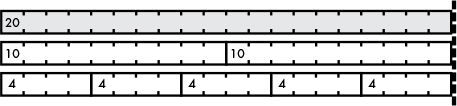
Figure 13-5: Cuisenaire rods demonstrating 4 and 10 are factors of 20
But 6 and 7 are not factors of 20, because the 6-square and 7-square rods won’t evenly fit into the 20-square rod, as shown in Figure 13-6.
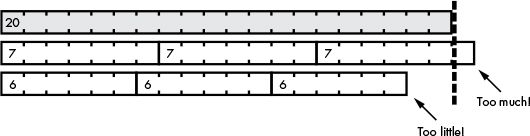
Figure 13-6: Cuisenaire rods demonstrating 6 and 7 are not factors of 20
The GCD of two rods, or two numbers represented by those rods, is the longest rod that can evenly fit into both rods, as shown in Figure 13-7.

Figure 13-7: Cuisenaire rods demonstrating the GCD of 16 and 24
In this example, the 8-square rod is the longest rod that can fit evenly into 24 and 32. Therefore, 8 is their GCD.
Now that you know how factors and the GCD work, let’s find the GCD of two numbers using a function we can write in Python.
The gcd() function we’ll write finds the GCD of two numbers. But before you learn how to code it, let’s look at a trick in Python called multiple assignment. The multiple assignment trick lets you assign values to more than one variable at once in a single assignment statement. Enter the following into the interactive shell to see how this works:
>>> spam, eggs = 42, 'Hello'
>>> spam
42
>>> eggs
'Hello'
>>> a, b, c, d = ['Alice', 'Brienne', 'Carol', 'Danielle']
>>> a
'Alice'
>>> d
'Danielle'
You can separate the variable names on the left side of the = operator as well as the values on the right side of the = operator using commas. You can also assign each of the values in a list to its own variable as long as the number of items in the list is the same as the number of variables on the left side of the = operator. If you don’t have the same number of variables as you have values, Python will raise an error that indicates the call needs more or has too many values.
One of the main uses of multiple assignment is to swap the values in two variables. Enter the following into the interactive shell to see an example:
>>> spam = 'hello'
>>> eggs = 'goodbye'
>>> spam, eggs = eggs, spam
>>> spam
'goodbye'
>>> eggs
'hello'
After assigning 'hello' to spam and 'goodbye' to eggs, we swap those values using multiple assignment. Let’s look at how to use this swapping trick to implement Euclid’s algorithm for finding the GCD.
Finding the GCD seems simple enough: identify all the factors of the two numbers you’ll use and then find the largest factor they have in common. But it isn’t so easy to find the GCD of larger numbers.
Euclid, a mathematician who lived 2000 years ago, came up with a short algorithm for finding the GCD of two numbers using modular arithmetic. Here’s a gcd() function that implements his algorithm in Python code, returning the GCD of integers a and b:
def gcd(a, b):
while a != 0:
a, b = b % a, a
return b
The gcd() function takes two numbers a and b, and then uses a loop and multiple assignment to find the GCD. Figure 13-8 shows how the gcd() function finds the GCD of 24 and 32.
Exactly how Euclid’s algorithm works is beyond the scope of this book, but you can rely on this function to return the GCD of the two integers you pass it. If you call this function from the interactive shell and pass it 24 and 32 for the parameters a and b, the function will return 8:
>>> gcd(24, 32)
8

Figure 13-8: How the gcd() function works
The great benefit of this gcd() function, though, is that it can easily handle large numbers:
>>> gcd(409119243, 87780243)
6837
This gcd() function will come in handy when choosing valid keys for the multiplicative and affine ciphers, as you’ll learn in the next section.
In the Caesar cipher, encrypting and decrypting symbols involved converting them to numbers, adding or subtracting the key, and then converting the new number back to a symbol.
When encrypting with the multiplicative cipher, you’ll multiply the index by the key. For example, if you encrypted the letter E with the key 3, you would find E’s index (4) and multiply it by the key (3) to get the index of the encrypted letter (4 × 3 = 12), which would be M.
When the product exceeds the total number of letters, the multiplicative cipher has a wraparound issue similar to the Caesar cipher, but now we can use the mod operator to solve that issue. For example, the Caesar cipher’s SYMBOLS variable contained the string 'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz1234567890 !?.'. The following is a table of the first and last few characters of SYMBOLS along with their indexes:

Let’s calculate what these symbols encrypt to when the key is 17. To encrypt the symbol F with key 17, multiply its index 5 by 17 and mod the result by 66 to handle the wraparound of the 66-symbol set. The result of (5 × 17) mod 66 is 19, and 19 corresponds to the symbol T. So F encrypts to T in the multiplicative cipher with key 17. The following two strings show all the characters in plaintext and their corresponding ciphertext symbols. The symbol at a given index in the first string encrypts to the symbol at that same index in the second string:
'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz1234567890 !?.'
'ARizCTk2EVm4GXo6IZq8Kbs0Mdu!Ofw.QhyBSj1DUl3FWn5HYp7Jar9Lct Nev?Pgx'
Compare this encryption output to the one you’d get when you encrypt using the Caesar cipher, which simply shifts the plaintext symbols over to create the ciphertext symbols:
'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz1234567890 !?.'
'RSTUVWXYZabcdefghijklmnopqrstuvwxyz1234567890 !?.ABCDEFGHIJKLMNOPQ'
As you can see, the multiplicative cipher with key 17 results in ciphertext that is more randomized and harder to crack. However, you’ll need to be careful when choosing keys for the multiplicative ciphers. I’ll discuss why next.
You can’t just use any number for the multiplicative cipher’s key. For example, if you chose the key 11, here’s the mapping you would end up with:
'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz1234567890 !?.'
'ALWhs4ALWhs4ALWhs4ALWhs4ALWhs4ALWhs4ALWhs4ALWhs4ALWhs4ALWhs4ALWhs4'
Notice that this key doesn’t work because the symbols A, G, and M all encrypt to the same letter, A. When you encounter an A in the ciphertext, you wouldn’t know which symbol it decrypts to. Using this key, you would run into the same problem when encrypting letters A, N, F, S, and others.
In the multiplicative cipher, the key and the size of the symbol set must be relatively prime to each other. Two numbers are relatively prime (or coprime) if their GCD is 1. In other words, they have no factors in common except 1. For example, the numbers num1 and num2 are relatively prime if gcd(num1, num2) == 1, where num1 is the key and num2 is the size of the symbol set. In the previous example, because 11 (the key) and 66 (the symbol set size) have a GCD that isn’t 1, they are not relatively prime, which means that the key 11 cannot be used for the multiplicative cipher. Note that numbers don’t actually have to be prime numbers to be relatively prime to each other.
Knowing how to use modular arithmetic and the gcd() function is important when using the multiplicative cipher. You can use the gcd() function to figure out whether a pair of numbers is relatively prime, which you need to know to choose valid keys for the multiplicative cipher.
The multiplicative cipher has only 20 different keys for a set of 66 symbols, even fewer than the Caesar cipher! However, you can combine the multiplicative cipher and the Caesar cipher to get the more powerful affine cipher, which I explain next.
One downside to using the multiplicative cipher is that the letter A always maps to the letter A. The reason is that A’s number is 0, and 0 multiplied by anything will always be 0. You can fix this issue by adding a second key to perform a Caesar cipher encryption after the multiplicative cipher’s multiplication and modding is done. This extra step changes the multiplicative cipher into the affine cipher.
The affine cipher has two keys: Key A and Key B. Key A is the integer you use to multiply the letter’s number. After you multiply the plaintext by Key A, you add Key B to the product. Then you mod the sum by 66, as you did in the original Caesar cipher. This means the affine cipher has 66 times as many possible keys as the multiplicative cipher. It also ensures that the letter A doesn’t always encrypt to itself.
The decryption process for the affine cipher mirrors the encryption process; both are shown in Figure 13-9.
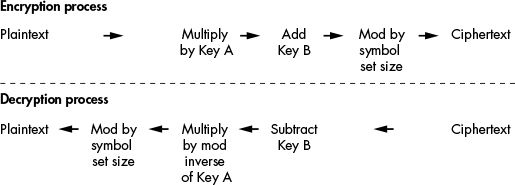
Figure 13-9: The affine cipher’s encryption and decryption processes
We decrypt the affine cipher using the opposite operations used for encryption. Let’s look at the decryption process and how to calculate the modular inverse in more detail.
In the Caesar cipher, you used addition to encrypt and subtraction to decrypt. In the affine cipher, you use multiplication to encrypt. Naturally, you might think you can divide to decrypt with the affine cipher. But if you try this, you’ll see that it doesn’t work. To decrypt with the affine cipher, you need to multiply by the key’s modular inverse. This reverses the mod operation from the encryption process.
A modular inverse of two numbers is represented by the expression (a * i) % m == 1, where i is the modular inverse and a and m are the two numbers. For example, the modular inverse of 5 mod 7 would be some number i where (5 * i) % 7 is equal to 1. You can brute-force this calculation like this:
1 isn’t the modular inverse of 5 mod 7, because (5 * 1) % 7 = 5.
2 isn’t the modular inverse of 5 mod 7, because (5 * 2) % 7 = 3.
3 is the modular inverse of 5 mod 7, because (5 * 3) % 7 = 1.
Although the encryption and decryption keys for the Caesar cipher part of the affine cipher are the same, the encryption key and decryption keys for the multiplicative cipher are two different numbers. The encryption key can be anything you choose as long as it’s relatively prime to the size of the symbol set, which in this case is 66. If you choose the key 53 for encrypting with the affine cipher, the decryption key is the modular inverse of 53 mod 66:
1 isn’t the modular inverse of 53 mod 66, because (53 * 1) % 66 = 53.
2 isn’t the modular inverse of 53 mod 66, because (53 * 2) % 66 = 40.
3 isn’t the modular inverse of 53 mod 66, because (53 * 3) % 66 = 27.
4 isn’t the modular inverse of 53 mod 66, because (53 * 4) % 66 = 14.
5 is the modular inverse of 53 mod 66, because (53 * 5) % 66 = 1.
Because 5 is the modular inverse of 53 and 66, you know that the affine cipher decryption key is also 5. To decrypt a ciphertext letter, multiply that letter’s number by 5 and then mod 66. The result is the number of the original plaintext’s letter.
Using the 66-character symbol set, let’s encrypt the word Cat using the key 53. C is at index 2, and 2 * 53 is 106, which is larger than the symbol set size, so we mod 106 by 66, and the result is 40. The character at index 40 in the symbol set is 'o', so the symbol C encrypts to o.
We’ll use the same steps for the next letter, a. The string 'a' is at index 26 in the symbol set, and 26 * 53 % 66 is 58, which is the index of '7'. So the symbol a encrypts to 7. The string 't' is at index 45, and 45 * 53 % 66 is 9, which is the index of 'J'. Therefore, the word Cat encrypts to o7J.
To decrypt, we multiply by the modular inverse of 53 % 66, which is 5. The symbol o is at index 40, and 40 * 5 % 66 is 2, which is the index of 'C'. The symbol 7 is at index 58, and 58 * 5 % 66 is 26, which is the index of 'a'. The symbol J is at index 9, and 9 * 5 % 66 is 45, which is the index of 't'. The ciphertext o7J decrypts to Cat, which is the original plaintext, just as expected.
To calculate the modular inverse to determine the decryption key, you could take a brute-force approach and start testing the integer 1, and then 2, and then 3, and so on. But this is time-consuming for large keys such as 8,953,851.
Fortunately, you can use Euclid’s extended algorithm to find the modular inverse of a number, which in Python looks like this:
def findModInverse(a, m):
if gcd(a, m) != 1:
return None # No mod inverse if a & m aren't relatively prime.
u1, u2, u3 = 1, 0, a
v1, v2, v3 = 0, 1, m
while v3 != 0:
q = u3 // v3 # Note that // is the integer division operator.
v1, v2, v3, u1, u2, u3 = (u1 - q * v1), (u2 - q * v2), (u3 - q * v3),
v1, v2, v3
return u1 % m
You don’t have to understand how Euclid’s extended algorithm works to use the findModInverse() function. As long as the two arguments you pass to the findModInverse() function are relatively prime, findModInverse() will return the modular inverse of the a parameter.
You can learn more about how Euclid’s extended algorithm works at https://www.nostarch.com/crackingcodes/.
You may have noticed the // operator used in the findModInverse() function in the preceding section. This is the integer division operator. It divides two numbers and rounds down to the nearest integer. Enter the following into the interactive shell to see how the // operator works:
>>> 41 / 7
5.857142857142857
>>> 41 // 7
5
>>> 10 // 5
2
Whereas 41 / 7 evaluates to 5.857142857142857, using 41 // 7 evaluates to 5. For division expressions that do not divide evenly, the // operator is useful for getting the whole number part of the answer (sometimes called the quotient), while the % operator gets the remainder. An expression that uses the // integer division operator always evaluates to an int, not a float. As you can see when evaluating 10 // 5, the result is 2 instead of 2.0.
We’ll use gcd() and findModInverse() in more cipher programs later in this book, so let’s put both functions into a module. Open a new file editor window, enter the following code, and save the file as cryptomath.py:
cryptomath.py
1. # Cryptomath Module
2. # https://www.nostarch.com/crackingcodes/ (BSD Licensed)
3.
4. def gcd(a, b):
5. # Return the GCD of a and b using Euclid's algorithm:
6. while a != 0:
7. a, b = b % a, a
8. return b
9.
10.
11. def findModInverse(a, m):
12. # Return the modular inverse of a % m, which is
13. # the number x such that a*x % m = 1.
14.
15. if gcd(a, m) != 1:
16. return None # No mod inverse if a & m aren't relatively prime.
17.
18. # Calculate using the extended Euclidean algorithm:
19. u1, u2, u3 = 1, 0, a
20. v1, v2, v3 = 0, 1, m
21. while v3 != 0:
22. q = u3 // v3 # Note that // is the integer division operator.
23. v1, v2, v3, u1, u2, u3 = (u1 - q * v1), (u2 - q * v2),
(u3 - q * v3), v1, v2, v3
24. return u1 % m
This program contains the gcd() function described earlier in this chapter and the findModInverse() function that implements Euclid’s extended algorithm.
After importing the cryptomath.py module, you can try out these functions from the interactive shell. Enter the following into the interactive shell:
>>> import cryptomath
>>> cryptomath.gcd(24, 32)
8
>>> cryptomath.gcd(37, 41)
1
>>> cryptomath.findModInverse(7, 26)
15
>>> cryptomath.findModInverse(8953851, 26)
17
As you can see, you can call the gcd() function and the findModInverse() function to find the GCD or modular inverse of two numbers.
This chapter covered some useful math concepts. The % operator finds the remainder after dividing one number by another. The gcd() function returns the largest number that can evenly divide two numbers. If the GCD of two numbers is 1, you know that those numbers are relatively prime to each other. The most useful algorithm to find the GCD of two numbers is Euclid’s algorithm.
Unlike the Caesar cipher, the affine cipher uses multiplication and addition instead of just addition to encrypt letters. However, not all numbers work as keys for the affine cipher. The key number and the size of the symbol set must be relatively prime to each other.
To decrypt with the affine cipher, you multiply the ciphertext’s index by the modular inverse of the key. The modular inverse of a % m is a number i such that (a * i) % m == 1. You can use Euclid’s extended algorithm to calculate modular inverses. Chapter 23’s public key cipher also uses modular inverses.
Using the math concepts you learned in this chapter, you’ll write a program for the affine cipher in Chapter 14. Because the multiplicative cipher is the same thing as the affine cipher using a Key B of 0, you won’t have a separate multiplicative cipher program. And because the multiplicative cipher is just a less secure version of the affine cipher, you shouldn’t use it anyway.