







Use this link to get 70% off the Automate the Boring Stuff online video course.
Support me on Patreon








“I believed then, and continue to believe now, that the benefits to our security and freedom of widely available cryptography far, far outweigh the inevitable damage that comes from its use by criminals and terrorists.”
—Matt Blaze, AT&T Labs, September 2001

The Italian cryptographer Giovan Battista Bellaso was the first person to describe the Vigenère cipher in 1553, but it was eventually named after the French diplomat Blaise de Vigenère, one of many people who reinvented the cipher in subsequent years. It was known as “le chiffre indéchiffrable,” which means “the indecipherable cipher,” and remained unbroken until British polymath Charles Babbage broke it in the 19th century.
Because the Vigenère cipher has too many possible keys to brute-force, even with our English detection module, it’s one of the strongest ciphers discussed so far in this book. It’s even invincible to the word pattern attack you learned in Chapter 17.
Unlike the Caesar cipher, the Vigenère cipher has multiple keys. Because it uses more than one set of substitutions, the Vigenère cipher is a polyalphabetic substitution cipher. Unlike with the simple substitution cipher, frequency analysis alone will not defeat the Vigenère cipher. Instead of using a numeric key between 0 and 25 as we did in the Caesar cipher, we use a letter key for the Vigenère.
The Vigenère key is a series of letters, such as a single English word, that is split into multiple single-letter subkeys that encrypt letters in the plaintext. For example, if we use a Vigenère key of PIZZA, the first subkey is P, the second subkey is I, the third and fourth subkeys are both Z, and the fifth subkey is A. The first subkey encrypts the first letter of the plaintext, the second subkey encrypts the second letter, and so on. When we get to the sixth letter of the plaintext, we return to the first subkey.
Using the Vigenère cipher is the same as using multiple Caesar ciphers, as shown in Figure 18-1. Instead of encrypting the whole plaintext with one Caesar cipher, we apply a different Caesar cipher to each letter of the plaintext.
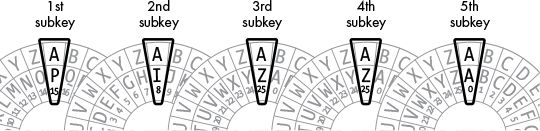
Figure 18-1: Multiple Caesar ciphers combine to make the Vigenère cipher
Each subkey is converted into an integer and serves as a Caesar cipher key. For example, the letter A corresponds to the Caesar cipher key 0. The letter B corresponds to key 1, and so on up to Z for key 25, as shown in Figure 18-2.

Figure 18-2: Caesar cipher keys and their corresponding letters
Let’s look at an example. The following is the message COMMON SENSE IS NOT SO COMMON shown alongside the Vigenère key PIZZA. The plaintext is shown with the corresponding subkey that encrypts each letter underneath it.
COMMONSENSEISNOTSOCOMMON
PIZZAPIZZAPIZZAPIZZAPIZZ
To encrypt the first C in the plaintext with the subkey P, encrypt it with the Caesar cipher using the subkey’s corresponding numeric key 15, which results in the cipherletter R, and repeat the process for each letter of the plaintext by cycling through the subkeys. Table 18-1 shows this process. The integer for the plaintext letter and subkey (given in parentheses) are added together to produce the integer for the ciphertext letter.
Table 18-1: Encrypting Letters with Vigenère Subkeys
Plaintext letter |
Subkey |
Ciphertext letter |
C (2) |
P (15) |
R (17) |
O (14) |
I (8) |
W (22) |
M (12) |
Z (25) |
L (11) |
M (12) |
Z (25) |
L (11) |
O (14) |
A (0) |
O (14) |
N (13) |
P (15) |
C (2) |
S (18) |
I (8) |
A (0) |
E (4) |
Z (25) |
D (3) |
N (13) |
Z (25) |
M (12) |
S (18) |
A (0) |
S (18) |
E (4) |
P (15) |
T (19) |
I (8) |
I (8) |
Q (16) |
S (18) |
Z (25) |
R (17) |
N (13) |
Z (25) |
M (12) |
O (14) |
A (0) |
O (14) |
T (19) |
P (15) |
I (8) |
S (18) |
I (8) |
A (0) |
O (14) |
Z (25) |
N (13) |
C (2) |
Z (25) |
B (1) |
O (14) |
A (0) |
O (14) |
M (12) |
P (15) |
B (1) |
M (12) |
I (8) |
U (20) |
O (14) |
Z (25) |
N (13) |
N (13) |
Z (25) |
M (12) |
Using the Vigenère cipher with the key PIZZA (which is made up of the subkeys 15, 8, 25, 25, 0) encrypts the plaintext COMMON SENSE IS NOT SO COMMON into the ciphertext RWLLOC ADMST QR MOI AN BOBUNM.
The more letters in the Vigenère key, the stronger the encrypted message will be against a brute-force attack. PIZZA is a poor choice for a Vigenère key because it has only five letters. A key with five letters has 11,881,376 possible combinations (because 26 letters to the power of 5 is 265 = 26 × 26 × 26 × 26 × 26 = 11,881,376). Eleven million keys are far too many for a human to brute-force, but a computer can try them all in just a few hours. It would first try to decrypt the message using the key AAAAA and check whether the resulting decryption was in English. Then it could try AAAAB, then AAAAC, and so on until it got to PIZZA.
The good news is that for every additional letter the key has, the number of possible keys multiplies by 26. Once there are quadrillions of possible keys, the cipher would take a computer many years to break. Table 18-2 shows how many possible keys there are for each key length.
Table 18-2: Number of Possible Keys Based on Vigenère Key Length
Key length |
Equation |
Possible keys |
1 |
26 |
= 26 |
2 |
26 × 26 |
= 676 |
3 |
676 × 26 |
= 17,576 |
4 |
17,576 × 26 |
= 456,976 |
5 |
456,976 × 26 |
= 11,881,376 |
6 |
11,881,376 × 26 |
= 308,915,776 |
7 |
308,915,776 × 26 |
= 8,031,810,176 |
8 |
8,031,810,176 × 26 |
= 208,827,064,576 |
9 |
208,827,064,576 × 26 |
= 5,429,503,678,976 |
10 |
5,429,503,678,976 × 26 |
= 141,167,095,653,376 |
11 |
141,167,095,653,376 × 26 |
= 3,670,344,486,987,776 |
12 |
3,670,344,486,987,776 × 26 |
= 95,428,956,661,682,176 |
13 |
95,428,956,661,682,176 × 26 |
= 2,481,152,873,203,736,576 |
14 |
2,481,152,873,203,736,576 × 26 |
= 64,509,974,703,297,150,976 |
With keys that are twelve or more letters long, it becomes impossible for a mere laptop to crack them in a reasonable amount of time.
A Vigenère key doesn’t have to be a real word like PIZZA. It can be any combination of letters of any length, such as the twelve-letter key DURIWKNMFICK. In fact, not using a word that can be found in the dictionary is best. Even though the word RADIOLOGISTS is also a twelve-letter key that is easier to remember than DURIWKNMFICK, a cryptanalyst might anticipate that the cryptographer is using an English word as a key.
Attempting a brute-force attack using every English word in the dictionary is known as a dictionary attack. There are 95,428,956,661,682,176 possible twelve-letter keys, but there are only about 1800 twelve-letter words in our dictionary file. If we use a twelve-letter word from the dictionary as a key, it would be easier to brute-force than a random three-letter key (which has 17,576 possible keys).
Of course, the cryptographer has an advantage in that the cryptanalyst doesn’t know the length of the Vigenère key. But the cryptanalyst could try all one-letter keys, then all two-letter keys, and so on, which would still allow them to find a dictionary word key very quickly.
Open a new file editor window by selecting File▸New File. Enter the following code into the file editor, save it as vigenereCipher.py, and make sure pyperclip.py is in the same directory. Press F5 to run the program.
vigenereCipher.py
1. # Vigenere Cipher (Polyalphabetic Substitution Cipher)
2. # https://www.nostarch.com/crackingcodes/ (BSD Licensed)
3.
4. import pyperclip
5.
6. LETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
7.
8. def main():
9. # This text can be downloaded from https://www.nostarch.com/
crackingcodes/:
10. myMessage = """Alan Mathison Turing was a British mathematician,
logician, cryptanalyst, and computer scientist."""
11. myKey = 'ASIMOV'
12. myMode = 'encrypt' # Set to either 'encrypt' or 'decrypt'.
13.
14. if myMode == 'encrypt':
15. translated = encryptMessage(myKey, myMessage)
16. elif myMode == 'decrypt':
17. translated = decryptMessage(myKey, myMessage)
18.
19. print('%sed message:' % (myMode.title()))
20. print(translated)
21. pyperclip.copy(translated)
22. print()
23. print('The message has been copied to the clipboard.')
24.
25.
26. def encryptMessage(key, message):
27. return translateMessage(key, message, 'encrypt')
28.
29.
30. def decryptMessage(key, message):
31. return translateMessage(key, message, 'decrypt')
32.
33.
34. def translateMessage(key, message, mode):
35. translated = [] # Stores the encrypted/decrypted message string.
36.
37. keyIndex = 0
38. key = key.upper()
39.
40. for symbol in message: # Loop through each symbol in message.
41. num = LETTERS.find(symbol.upper())
42. if num != -1: # -1 means symbol.upper() was not found in LETTERS.
43. if mode == 'encrypt':
44. num += LETTERS.find(key[keyIndex]) # Add if encrypting.
45. elif mode == 'decrypt':
46. num -= LETTERS.find(key[keyIndex]) # Subtract if
decrypting.
47.
48. num %= len(LETTERS) # Handle any wraparound.
49.
50. # Add the encrypted/decrypted symbol to the end of translated:
51. if symbol.isupper():
52. translated.append(LETTERS[num])
53. elif symbol.islower():
54. translated.append(LETTERS[num].lower())
55.
56. keyIndex += 1 # Move to the next letter in the key.
57. if keyIndex == len(key):
58. keyIndex = 0
59. else:
60. # Append the symbol without encrypting/decrypting:
61. translated.append(symbol)
62.
63. return ''.join(translated)
64.
65.
66. # If vigenereCipher.py is run (instead of imported as a module), call
67. # the main() function:
68. if __name__ == '__main__':
69. main()
When you run the program, its output will look like this:
Encrypted message:
Adiz Avtzqeci Tmzubb wsa m Pmilqev halpqavtakuoi, lgouqdaf, kdmktsvmztsl, izr
xoexghzr kkusitaaf.
The message has been copied to the clipboard.
The program prints the encrypted message and copies the encrypted text to the clipboard.
The beginning of the program has the usual comments describing the program, an import statement for the pyperclip module, and a variable called LETTERS that holds a string of every uppercase letter. The main() function for the Vigenère cipher is like the other main() functions in this book: it starts by defining the variables for message, key, and mode.
1. # Vigenere Cipher (Polyalphabetic Substitution Cipher)
2. # https://www.nostarch.com/crackingcodes/ (BSD Licensed)
3.
4. import pyperclip
5.
6. LETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
7.
8. def main():
9. # This text can be downloaded from https://www.nostarch.com/
crackingcodes/:
10. myMessage = """Alan Mathison Turing was a British mathematician,
logician, cryptanalyst, and computer scientist."""
11. myKey = 'ASIMOV'
12. myMode = 'encrypt' # Set to either 'encrypt' or 'decrypt'.
13.
14. if myMode == 'encrypt':
15. translated = encryptMessage(myKey, myMessage)
16. elif myMode == 'decrypt':
17. translated = decryptMessage(myKey, myMessage)
18.
19. print('%sed message:' % (myMode.title()))
20. print(translated)
21. pyperclip.copy(translated)
22. print()
23. print('The message has been copied to the clipboard.')
The user sets these variables on lines 10, 11, and 12 before running the program. The encrypted or decrypted message (depending on what myMode is set to) is stored in a variable named translated so it can be printed to the screen (line 20) and copied to the clipboard (line 21).
Almost all the programs in this book have built a string with code in some form. That is, the program creates a variable that starts as a blank string and then adds characters using string concatenation. This is what the previous cipher programs have done with the translated variable. Open the interactive shell and enter the following code:
>>> building = ''
>>> for c in 'Hello world!':
>>> building += c
>>> print(building)
This code loops through each character in the string 'Hello world!' and concatenates it to the end of the string stored in building. At the end of the loop, building holds the complete string.
Although string concatenation seems like a straightforward technique, it’s very inefficient in Python. It’s much faster to start with a blank list and then use the append() list method. When you’re done building the list of strings, you can convert the list to a single string value using the join() method. The following code does the same thing as the previous example, but faster. Enter the code into the interactive shell:
>>> building = []
>>> for c in 'Hello world!':
>>> building.append(c)
>>> building = ''.join(building)
>>> print(building)
Using this approach to build up strings instead of modifying a string will result in much faster programs. You can see the difference by timing the two approaches using time.time(). Open a new file editor window and enter the following code:
stringTest.py
import time
startTime = time.time()
for trial in range(10000):
building = ''
for i in range(10000):
building += 'x'
print('String concatenation: ', (time.time() - startTime))
startTime = time.time()
for trial in range(10000):
building = []
for i in range(10000):
building.append('x')
building = ''.join(building)
print('List appending: ', (time.time() - startTime))
Save this program as stringTest.py and run it. The output will look something like this:
String concatenation: 40.317070960998535
List appending: 10.488219022750854
The program stringTest.py sets a variable startTime as the current time, runs code to append 10,000 characters to a string using concatenation, and then prints the time it took to finish the concatenation. Then the program resets startTime to the current time, runs code to use the list-appending method to build a string of the same length, and then prints the total time it took to finish. On my computer, using string concatenation to build 10,000 strings that are 10,000 characters each took about 40 seconds, but using the list-append-join process to do the same task took only 10 seconds. If your program builds a lot of strings, using lists can make your program much faster.
We’ll use the list-append-join process to build strings for the remaining programs in this book.
Because the encryption and decryption code is mostly the same, we’ll create two wrapper functions called encryptMessage() and decryptMessage() for the function translateMessage(), which will hold the actual code to encrypt and decrypt.
26. def encryptMessage(key, message):
27. return translateMessage(key, message, 'encrypt')
28.
29.
30. def decryptMessage(key, message):
31. return translateMessage(key, message, 'decrypt')
The translateMessage() function builds the encrypted (or decrypted) string one character at a time. The list in translated stores these characters so they can be joined when the string building is done.
34. def translateMessage(key, message, mode):
35. translated = [] # Stores the encrypted/decrypted message string.
36.
37. keyIndex = 0
38. key = key.upper()
Keep in mind that the Vigenère cipher is just the Caesar cipher except a different key is used depending on the position of the letter in the message. The keyIndex variable, which keeps track of which subkey to use, starts at 0 because the letter used to encrypt or decrypt the first character of the message is key[0].
The program assumes that the key is in all uppercase letters. To make sure the key is valid, line 38 calls upper() on key.
The rest of the code in translateMessage() is similar to the Caesar cipher code:
40. for symbol in message: # Loop through each symbol in message.
41. num = LETTERS.find(symbol.upper())
42. if num != -1: # -1 means symbol.upper() was not found in LETTERS.
43. if mode == 'encrypt':
44. num += LETTERS.find(key[keyIndex]) # Add if encrypting.
45. elif mode == 'decrypt':
46. num -= LETTERS.find(key[keyIndex]) # Subtract if
decrypting.
The for loop on line 40 sets the characters in message to the variable symbol on each iteration of the loop. Line 41 finds the index of the uppercase version of symbol in LETTERS, which is how we translate a letter into a number.
If num isn’t set to -1 on line 41, the uppercase version of symbol was found in LETTERS (meaning that symbol is a letter). The keyIndex variable keeps track of which subkey to use, and the subkey is always what key[keyIndex] evaluates to.
Of course, this is just a single letter string. We need to find this letter’s index in LETTERS to convert the subkey to an integer. This integer is then added (if encrypting) to the symbol’s number on line 44 or subtracted (if decrypting) to the symbol’s number on line 46.
In the Caesar cipher code, we checked whether the new value of num was less than 0 (in which case, we added len(LETTERS) to it) or whether the new value of num was len(LETTERS) or greater (in which case, we subtracted len(LETTERS) from it). These checks handle the wraparound cases.
However, there is a simpler way to handle both of these cases. If we mod the integer stored in num by len(LETTERS), we can accomplish the same calculation in a single line of code:
48. num %= len(LETTERS) # Handle any wraparound.
For example, if num was -8, we’d want to add 26 (that is, len(LETTERS)) to it to get 18, and that can be expressed as -8 % 26, which evaluates to 18. Or if num was 31, we’d want to subtract 26 to get 5, and 31 % 26 evaluates to 5. The modular arithmetic on line 48 handles both wraparound cases.
The encrypted (or decrypted) character exists at LETTERS[num]. However, we want the encrypted (or decrypted) character’s case to match the original case of symbol.
50. # Add the encrypted/decrypted symbol to the end of translated:
51. if symbol.isupper():
52. translated.append(LETTERS[num])
53. elif symbol.islower():
54. translated.append(LETTERS[num].lower())
So if symbol is an uppercase letter, the condition on line 51 is True, and line 52 appends the character at LETTERS[num] to translated because all the characters in LETTERS are already in uppercase.
However, if symbol is a lowercase letter, the condition on line 53 is True instead, and line 54 appends the lowercase form of LETTERS[num] to translated. This is how we make the encrypted (or decrypted) message match the original message casing.
Now that we’ve translated the symbol, we want to ensure that on the next iteration of the for loop, we use the next subkey. Line 56 increments keyIndex by 1, so the next iteration uses the index of the next subkey:
56. keyIndex += 1 # Move to the next letter in the key.
57. if keyIndex == len(key):
58. keyIndex = 0
However, if we were on the last subkey in the key, keyIndex would be equal to the length of key. Line 57 checks for this condition and resets keyIndex back to 0 on line 58 if that’s the case so that key[keyIndex] points back to the first subkey.
The indentation indicates that the else statement on line 59 is paired with the if statement on line 42:
59. else:
60. # Append the symbol without encrypting/decrypting:
61. translated.append(symbol)
The code on line 61 executes if the symbol was not found in the LETTERS string. This happens if symbol is a number or punctuation mark, such as '5' or '?'. In this case, line 61 appends the unmodified symbol to translated.
Now that we’re done building the string in translated, we call the join() method on the blank string:
63. return ''.join(translated)
This line makes the function return the whole encrypted or decrypted message when the function is called.
Lines 68 and 69 finish the program’s code:
68. if __name__ == '__main__':
69. main()
These lines call the main() function if the program was run by itself rather than being imported by another program that wants to use its encryptMessage() and decryptMessage() functions.
You’re close to the end of this book, but notice that the Vigenère cipher isn’t that much more complicated than the Caesar cipher, which was one of the first cipher programs you learned. With just a few changes to the Caesar cipher, we created a cipher that has exponentially more possible keys than can be brute-forced.
The Vigenère cipher isn’t vulnerable to the dictionary word pattern attack that the simple substitution hacker program uses. For hundreds of years, the “indecipherable” Vigenère cipher kept messages secret, but this cipher, too, eventually became vulnerable. In Chapters 19 and 20, you’ll learn frequency analysis techniques that will enable you to hack the Vigenère cipher.