







Use this link to get 70% off the Automate the Boring Stuff online video course.
Support me on Patreon








“The ineffable talent for finding patterns in chaos cannot do its thing unless he immerses himself in the chaos first. If they do contain patterns, he does not see them just now, in any rational way. But there may be some subrational part of his mind that can go to work . . .”
—Neal Stephenson, Cryptonomicon

In this chapter, you’ll learn how to determine the frequency of each English letter in a particular text. You’ll then compare these frequencies to the letter frequencies of your ciphertext to get information about the original plaintext, which will help you break the encryption. This process of determining how frequently a letter appears in plaintexts and in ciphertexts is called frequency analysis. Understanding frequency analysis is an important step in hacking the Vigenère cipher. We’ll use letter frequency analysis to break the Vigenère cipher in Chapter 20.
When you flip a coin, about half the time it comes up heads and half the time it comes up tails. That is, the frequency of heads and tails should be about the same. We can represent the frequency as a percentage by dividing the total number of times an event occurs (how many times we flip a heads, for example) by the total number of attempts at an event (which is the total number of times we flipped the coin) and multiplying the quotient by 100. We can learn much about a coin from its frequency of heads or tails: whether the coin is fair or unfairly weighted or even if it’s a two-headed coin.
We can also learn much about a ciphertext from the frequency of its letters. Some letters in the English alphabet are used more often than others. For example, the letters E, T, A, and O appear most frequently in English words, whereas the letters J, X, Q, and Z appear less frequently in English. We’ll use this difference in letter frequencies in the English language to crack Vigenère-encrypted messages.
Figure 19-1 shows the letter frequencies found in standard English. The graph was compiled using text from books, newspapers, and other sources.
When we sort these letter frequencies in order of greatest frequency to least, E is the most frequent letter, followed by T, then A, and so on, as shown in Figure 19-2.
The six most frequently occurring letters in English are ETAOIN. The full list of letters ordered by frequency is ETAOINSHRDLCUMWFGYPBVKJXQZ.
Recall that the transposition cipher encrypts messages by arranging the letters of the original English plaintext in a different order. This means that the letter frequencies in the ciphertext are no different from those in the original plaintext. For example, E, T, and A should appear more often than Q and Z in a transposition ciphertext.
Likewise, the letters that appear most often in a Caesar ciphertext and a simple substitution ciphertext are more likely to have been encrypted from the most commonly found English letters, such as E, T, or A. Similarly, the letters that appear least often in the ciphertext are more likely to have been encrypted from to X, Q, and Z in plaintext.
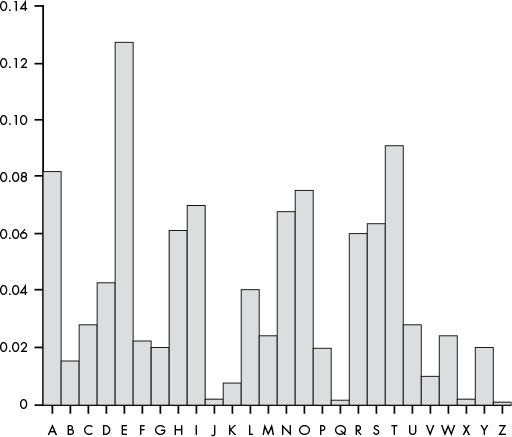
Figure 19-1: Frequency analysis of each letter in typical English text
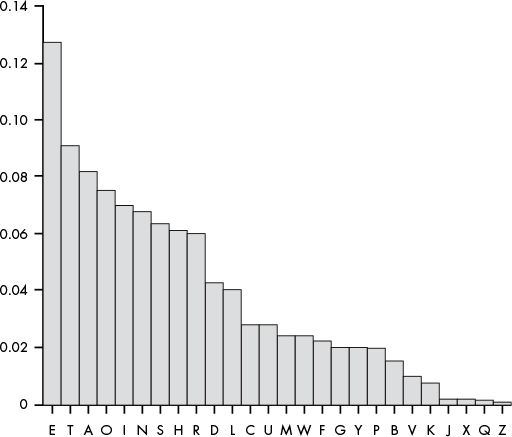
Figure 19-2: Most frequent and least frequent letters in typical English text
Frequency analysis is very useful when hacking the Vigenère cipher because it lets us brute-force each subkey one at a time. For example, if a message was encrypted with the key PIZZA, we would need to brute-force 265 or 11,881,376 keys to find the entire key at once. To brute-force only one of the five subkeys, however, we only need to try 26 possibilities. Doing this for each of the five subkeys means we only need to brute-force 26 × 5 or 130 subkeys.
Using the key PIZZA, every fifth letter in the message starting with the first letter would be encrypted with P, every fifth letter starting with the second letter with I, and so on. We can brute-force for the first subkey by decrypting every fifth letter in the ciphertext with all 26 possible subkeys. For the first subkey, we would find that P produced decrypted letters that matched the letter frequency of English more than the other 25 possible subkeys. This would be a strong indicator that P was the first subkey. We could then repeat this for the other subkeys until we had the entire key.
To find the letter frequencies in a message, we’ll use an algorithm that simply orders the letters in a string by highest frequency to lowest frequency. Then the algorithm uses this ordered string to calculate what this book calls a frequency match score, which we’ll use to determine how similar a string’s letter frequency is to that of standard English.
To calculate the frequency match score for a ciphertext, we start with 0 and then add a point each time one of the most frequent English letters (E, T, A, O, I, N) appears among the six most frequent letters of the ciphertext. We’ll also add a point to the score each time one of the least frequent letters (V, K, J, X, Q, or Z) appears among the six least frequent letters of the ciphertext.
The frequency match score for a string can range from 0 (the string’s letter frequency is completely unlike the English letter frequency) to 12 (the string’s letter frequency is identical to that of regular English). Knowing the frequency match score of a ciphertext can reveal important information about the original plaintext.
We’ll use the following ciphertext to calculate the frequency match score of a message encrypted using the simple substitution cipher:
Sy l nlx sr pyyacao l ylwj eiswi upar lulsxrj isr sxrjsxwjr, ia esmm
rwctjsxsza sj wmpramh, lxo txmarr jia aqsoaxwa sr pqaceiamnsxu, ia esmm caytra
jp famsaqa sj. Sy, px jia pjiac ilxo, ia sr pyyacao rpnajisxu eiswi lyypcor
l calrpx ypc lwjsxu sx lwwpcolxwa jp isr sxrjsxwjr, ia esmm lwwabj sj aqax
px jia rmsuijarj aqsoaxwa. Jia pcsusx py nhjir sr agbmlsxao sx jisr elh.
-Facjclxo Ctrramm
When we count the frequency of each letter in this ciphertext and sort from highest to lowest frequency, the result is ASRXJILPWMCYOUEQNTHBFZGKVD. A is the most frequent letter, S is the second most frequent letter, and so on to the letter D, which appears least frequently.
Of the six most frequent letters in this example (A, S, R, X, J, and I), two of these letters (A and I) are also among the six most frequently appearing letters in the English language, which are E, T, A, O, I, and N. So we add two points to the frequency match score.
The six least frequent letters in the ciphertext are F, Z, G, K, V, and D. Three of these letters (Z, K, and V) appear in the set of least frequently occurring letters, which are V, K, J, X, Q, and Z. So we add three more points to the score. Based on the frequency ordering derived from this ciphertext, ASRXJILPWMCYOUEQNTHBFZGKVD, the frequency match score is 5, as shown in Figure 19-3.

Figure 19-3: Calculating the frequency match score of the simple substitution cipher
The ciphertext encrypted using a simple substitution cipher won’t have a very high frequency match score. The letter frequencies of a simple substitution ciphertext don’t match those of regular English because the plaintext letters are substituted one for one with cipherletters. For example, if the letter T is encrypted to the letter J, then J would be more likely to appear frequently in the ciphertext, even though it’s one of the least frequently appearing letters in English.
This time let’s calculate the frequency match score for a ciphertext encrypted using the transposition cipher:
"I rc ascwuiluhnviwuetnh,osgaa ice tipeeeee slnatsfietgi tittynecenisl. e
fo f fnc isltn sn o a yrs sd onisli ,l erglei trhfmwfrogotn,l stcofiit.
aea wesn,lnc ee w,l eIh eeehoer ros iol er snh nl oahsts ilasvih tvfeh
rtira id thatnie.im ei-dlmf i thszonsisehroe, aiehcdsanahiec gv gyedsB
affcahiecesd d lee onsdihsoc nin cethiTitx eRneahgin r e teom fbiotd n
ntacscwevhtdhnhpiwru"
The most frequent to least frequent letters in this ciphertext are EISNTHAOCLRFDGWVMUYBPZXQJK. E is the most frequent letter, I is the second most frequent letter, and so on.
The four most frequently appearing letters in this ciphertext (E, I, N, and T) also happen to be among the most frequent letters in standard English (ETAOIN). Similarly, the five least frequent letters in the ciphertext (Z, X, Q, J, and K) also appear in VKJXQZ, resulting in a total frequency match score of 9, as shown in Figure 19-4.

Figure 19-4: Calculating the frequency match score of the transposition cipher
The ciphertext encrypted using a transposition cipher should have a much higher frequency match score than a simple substitution ciphertext. The reason is that unlike the simple substitution cipher, the transposition cipher uses the same letters found in the original plaintext but arranged in a different order. Therefore, the frequency of each letter remains the same.
To hack the Vigenère cipher, we need to decrypt the subkeys individually. That means we can’t rely on using English word detection, because we won’t be able to decrypt enough of the message using just one subkey.
Instead, we’ll decrypt the letters encrypted with one subkey and perform frequency analysis to determine which decrypted ciphertext produces a letter frequency that most closely matches that of regular English. In other words, we need to find which decryption has the highest frequency match score, which is a good indication that we’ve found the correct subkey.
We repeat this process for the second, third, fourth, and fifth subkey as well. For now, we’re just guessing that the key length is five letters. (In Chapter 20, you’ll learn how to use Kasiski examination to determine the key length.) Because there are 26 decryptions for each subkey (the total number of letters in the alphabet) in the Vigenère cipher, the computer only has to perform 26 + 26 + 26 + 26 + 26, or 156, decryptions for a five-letter key. This is much easier than performing decryptions for every possible subkey combination, which would total 11,881,376 decryptions (26 × 26 × 26 × 26 × 26)!
There are more steps to hack the Vigenère cipher, which you’ll learn in Chapter 20 when we write the hacking program. For now, let’s write a module that performs frequency analysis using the following helpful functions:
getLetterCount() Takes a string parameter and returns a dictionary that has the count of how often each letter appears in the string
getFrequencyOrder() Takes a string parameter and returns a string of the 26 letters ordered from most frequent to least frequent in the string parameter
englishFreqMatchScore() Takes a string parameter and returns an integer from 0 to 12, indicating a letter’s frequency match score
Open a new file editor window by selecting File▸New File. Enter the following code into the file editor, save it as freqAnalysis.py, and make sure pyperclip.py is in the same directory. Press F5 to run the program.
freqAnalysis.py
1. # Frequency Finder
2. # https://www.nostarch.com/crackingcodes/ (BSD Licensed)
3.
4. ETAOIN = 'ETAOINSHRDLCUMWFGYPBVKJXQZ'
5. LETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
6.
7. def getLetterCount(message):
8. # Returns a dictionary with keys of single letters and values of the
9. # count of how many times they appear in the message parameter:
10. letterCount = {'A': 0, 'B': 0, 'C': 0, 'D': 0, 'E': 0, 'F': 0,
'G': 0, 'H': 0, 'I': 0, 'J': 0, 'K': 0, 'L': 0, 'M': 0, 'N': 0,
'O': 0, 'P': 0, 'Q': 0, 'R': 0, 'S': 0, 'T': 0, 'U': 0, 'V': 0,
'W': 0, 'X': 0, 'Y': 0, 'Z': 0}
11.
12. for letter in message.upper():
13. if letter in LETTERS:
14. letterCount[letter] += 1
15.
16. return letterCount
17.
18.
19. def getItemAtIndexZero(items):
20. return items[0]
21.
22.
23. def getFrequencyOrder(message):
24. # Returns a string of the alphabet letters arranged in order of most
25. # frequently occurring in the message parameter.
26.
27. # First, get a dictionary of each letter and its frequency count:
28. letterToFreq = getLetterCount(message)
29.
30. # Second, make a dictionary of each frequency count to the letter(s)
31. # with that frequency:
32. freqToLetter = {}
33. for letter in LETTERS:
34. if letterToFreq[letter] not in freqToLetter:
35. freqToLetter[letterToFreq[letter]] = [letter]
36. else:
37. freqToLetter[letterToFreq[letter]].append(letter)
38.
39. # Third, put each list of letters in reverse "ETAOIN" order, and then
40. # convert it to a string:
41. for freq in freqToLetter:
42. freqToLetter[freq].sort(key=ETAOIN.find, reverse=True)
43. freqToLetter[freq] = ''.join(freqToLetter[freq])
44.
45. # Fourth, convert the freqToLetter dictionary to a list of
46. # tuple pairs (key, value), and then sort them:
47. freqPairs = list(freqToLetter.items())
48. freqPairs.sort(key=getItemAtIndexZero, reverse=True)
49.
50. # Fifth, now that the letters are ordered by frequency, extract all
51. # the letters for the final string:
52. freqOrder = []
53. for freqPair in freqPairs:
54. freqOrder.append(freqPair[1])
55.
56. return ''.join(freqOrder)
57.
58.
59. def englishFreqMatchScore(message):
60. # Return the number of matches that the string in the message
61. # parameter has when its letter frequency is compared to English
62. # letter frequency. A "match" is how many of its six most frequent
63. # and six least frequent letters are among the six most frequent and
64. # six least frequent letters for English.
65. freqOrder = getFrequencyOrder(message)
66.
67. matchScore = 0
68. # Find how many matches for the six most common letters there are:
69. for commonLetter in ETAOIN[:6]:
70. if commonLetter in freqOrder[:6]:
71. matchScore += 1
72. # Find how many matches for the six least common letters there are:
73. for uncommonLetter in ETAOIN[-6:]:
74. if uncommonLetter in freqOrder[-6:]:
75. matchScore += 1
76.
77. return matchScore
Line 4 creates a variable named ETAOIN, which stores the 26 letters of the alphabet ordered from most to least frequent:
1. # Frequency Finder
2. # https://www.nostarch.com/crackingcodes/ (BSD Licensed)
3.
4. ETAOIN = 'ETAOINSHRDLCUMWFGYPBVKJXQZ'
Of course, not all English text reflects this exact frequency ordering. You could easily find a book that has a set of letter frequencies where Z is used more often than Q. For example, the novel Gadsby by Ernest Vincent Wright never uses the letter E, which gives it an odd set of letter frequencies. But in most cases, including in our module, the ETAOIN order should be accurate enough.
The module also needs a string of all the uppercase letters in alphabetical order for a few different functions, so we set the LETTERS constant variable on line 5.
5. LETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
LETTERS serves the same purpose as the SYMBOLS variables did in our previous programs: providing a mapping between string letters and integer indexes.
Next, we’ll look at how the getLettersCount() function counts the frequency of each letter stored in the message string.
The getLetterCount() function takes the message string and returns a dictionary value whose keys are single uppercase letter strings and whose values are integers that store the number of times that letter occurs in the message parameter.
Line 10 creates the letterCount variable by assigning to it a dictionary that has all keys set to an initial value of 0:
7. def getLetterCount(message):
8. # Returns a dictionary with keys of single letters and values of the
9. # count of how many times they appear in the message parameter:
10. letterCount = {'A': 0, 'B': 0, 'C': 0, 'D': 0, 'E': 0, 'F': 0,
'G': 0, 'H': 0, 'I': 0, 'J': 0, 'K': 0, 'L': 0, 'M': 0, 'N': 0,
'O': 0, 'P': 0, 'Q': 0, 'R': 0, 'S': 0, 'T': 0, 'U': 0, 'V': 0,
'W': 0, 'X': 0, 'Y': 0, 'Z': 0}
We increment the values associated with the keys until they represent the counts of each letter by checking each character in message using a for loop on line 12.
12. for letter in message.upper():
13. if letter in LETTERS:
14. letterCount[letter] += 1
The for loop iterates through each character in the uppercase version of message and assigns the character to the letter variable. On line 13, we check whether the character exists in the LETTERS string, because we don’t want to count the non-letter characters in message. When the letter is part of the LETTERS string, line 14 increments the value at letterCount[letter].
After the for loop on line 12 finishes, the letterCount dictionary on line 16 should have a count showing how often each letter appeared in message. This dictionary is returned from getLetterCount():
16. return letterCount
For example, in this chapter we’ll use the following string (from https://en.wikipedia.org/wiki/Alan_Turing):
"""Alan Mathison Turing was a British mathematician, logician, cryptanalyst, and computer
scientist. He was highly influential in the development of computer science, providing a
formalisation of the concepts of "algorithm" and "computation" with the Turing machine. Turing
is widely considered to be the father of computer science and artificial intelligence. During
World War II, Turing worked for the Government Code and Cypher School (GCCS) at Bletchley Park,
Britain's codebreaking centre. For a time he was head of Hut 8, the section responsible for
German naval cryptanalysis. He devised a number of techniques for breaking German ciphers,
including the method of the bombe, an electromechanical machine that could find settings
for the Enigma machine. After the war he worked at the National Physical Laboratory, where
he created one of the first designs for a stored-program computer, the ACE. In 1948 Turing
joined Max Newman's Computing Laboratory at Manchester University, where he assisted in the
development of the Manchester computers and became interested in mathematical biology. He wrote
a paper on the chemical basis of morphogenesis, and predicted oscillating chemical reactions
such as the Belousov-Zhabotinsky reaction, which were first observed in the 1960s. Turing's
homosexuality resulted in a criminal prosecution in 1952, when homosexual acts were still
illegal in the United Kingdom. He accepted treatment with female hormones (chemical castration)
as an alternative to prison. Turing died in 1954, just over two weeks before his 42nd birthday,
from cyanide poisoning. An inquest determined that his death was suicide; his mother and some
others believed his death was accidental. On 10 September 2009, following an Internet campaign,
British Prime Minister Gordon Brown made an official public apology on behalf of the British
government for "the appalling way he was treated." As of May 2012 a private member's bill was
before the House of Lords which would grant Turing a statutory pardon if enacted."""
For this string value, which has 135 instances of A, 30 instances of B, and so on, getLetterCount() would return a dictionary that looks like this:
{'A': 135, 'B': 30, 'C': 74, 'D': 58, 'E': 196, 'F': 37, 'G': 39, 'H': 87,
'I': 139, 'J': 2, 'K': 8, 'L': 62, 'M': 58, 'N': 122, 'O': 113, 'P': 36,
'Q': 2, 'R': 106, 'S': 89, 'T': 140, 'U': 37, 'V': 14, 'W': 30, 'X': 3,
'Y': 21, 'Z': 1}
The getItemAtIndexZero() function on line 19 returns the items at index 0 when a tuple is passed to it:
19. def getItemAtIndexZero(items):
20. return items[0]
Later in the program, we’ll pass this function to the sort() method to sort the frequencies of the letters into numerical order. We’ll look at this in detail in “Converting the Dictionary Items to a Sortable List” on page 275.
The getFrequencyOrder() function takes a message string as an argument and returns a string with the 26 uppercase letters of the alphabet arranged by how frequently they appear in the message parameter. If message is readable English instead of random gibberish, it’s likely that this string will be similar, if not identical, to the string in the ETAOIN constant. The code in the getFrequencyOrder() function does most of the work of calculating a string’s frequency match score, which we’ll use in the Vigenère hacking program in Chapter 20.
For example, if we pass the """Alan Mathison Turing...""" string to getFrequencyOrder(), the function would return the string 'ETIANORSHCLMDGFUPBWYVKXQJZ' because E is the most common letter in that string, followed by T, then I, then A, and so on.
The getFrequencyOrder() function consists of five steps:
Counting the letters in the string
Creating a dictionary of frequency counts and letter lists
Sorting the letter lists in reverse ETAOIN order
Converting this data to a list of tuples
Converting the list into the final string to return from the function getFrequencyOrder()
Let’s look at each step in turn.
The first step of getFrequencyOrder() calls getLetterCount() on line 28 with the message parameter to get a dictionary, named letterToFreq, containing the count of every letter in message:
23. def getFrequencyOrder(message):
24. # Returns a string of the alphabet letters arranged in order of most
25. # frequently occurring in the message parameter.
26.
27. # First, get a dictionary of each letter and its frequency count:
28. letterToFreq = getLetterCount(message)
If we pass the """Alan Mathison Turing...""" string as the message parameter, line 28 assigns letterToFreq the following dictionary value:
{'A': 135, 'C': 74, 'B': 30, 'E': 196, 'D': 58, 'G': 39, 'F': 37, 'I': 139,
'H': 87, 'K': 8, 'J': 2, 'M': 58, 'L': 62, 'O': 113, 'N': 122, 'Q': 2,
'P': 36, 'S': 89, 'R': 106, 'U': 37, 'T': 140, 'W': 30, 'V': 14, 'Y': 21,
'X': 3, 'Z': 1}
The second step of getFrequencyOrder() creates a dictionary, freqToLetter, whose keys are the frequency count and whose values are a list of letters with those frequency counts. Whereas the letterToFreq dictionary maps letter keys to frequency values, the freqToLetter dictionary maps frequency keys to the list of letter values, so we’ll need to flip the key and values in the letterToFreq dictionary. We flip the keys and values because multiple letters could have the same frequency count: 'B' and 'W' both have a frequency count of 30 in our example, so we need to put them in a dictionary that looks like {30: ['B', 'W']} because dictionary keys must be unique. Otherwise, a dictionary value that looks like {30: 'B', 30: 'W'} will simply overwrite one of these key-value pairs with the other.
To make the freqToLetter dictionary, line 32 first creates a blank dictionary:
30. # Second, make a dictionary of each frequency count to the letter(s)
31. # with that frequency:
32. freqToLetter = {}
33. for letter in LETTERS:
34. if letterToFreq[letter] not in freqToLetter:
35. freqToLetter[letterToFreq[letter]] = [letter]
36. else:
37. freqToLetter[letterToFreq[letter]].append(letter)
Line 33 loops over all the letters in LETTERS, and the if statement on line 34 checks whether the letter’s frequency, or letterToFreq[letter], already exists as a key in freqToLetter. If not, then line 35 adds this key with a list of the letter as the value. If the letter’s frequency already exists as a key in freqToLetter, line 37 simply appends the letter to the end of the list already in letterToFreq[letter].
Using the example value of letterToFreq created using the """Alan Mathison Turing...""" string, freqToLetter should now return something like this:
{1: ['Z'], 2: ['J', 'Q'], 3: ['X'], 135: ['A'], 8: ['K'], 139: ['I'],
140: ['T'], 14: ['V'], 21: ['Y'], 30: ['B', 'W'], 36: ['P'], 37: ['F', 'U'],
39: ['G'], 58: ['D', 'M'], 62: ['L'], 196: ['E'], 74: ['C'], 87: ['H'],
89: ['S'], 106: ['R'], 113: ['O'], 122: ['N']}
Notice that the dictionary’s keys now contain the frequency counts and its values contain lists of letters that have those frequencies.
The third step of getFrequencyOrder() involves sorting the letter strings in each list of freqToLetter. Recall that freqToLetter[freq] evaluates to a list of letters that has a frequency count of freq. We use a list because it’s possible for two or more letters to have the same frequency count, in which case the list would have strings made up of two or more letters.
When multiple letters have the same frequency counts, we want to sort those letters in reverse order compared to the order in which they appear in the ETAOIN string. This makes the ordering consistent and minimizes the likelihood of increasing the frequency match score by chance.
For example, let’s say the frequency counts for the letters V, I, N, and K are all the same for a string we’re trying to score. Let’s also say that four letters in the string have higher frequency counts than V, I, N, and K and eighteen letters have lower frequency counts. I’ll just use x as a placeholder for these letters in this example. Figure 19-5 shows what putting these four letters in ETAOIN order would look like.

Figure 19-5: The frequency match score will gain two points if the four letters are in ETAOIN order.
The I and N add two points to the frequency match score in this case because I and N are among the top six most frequent letters, even though they don’t appear more frequently than V and K in this example string. Because the frequency match scores only range from 0 to 12, these two points can make quite a difference! But by putting letters of identical frequency in reverse ETAOIN order, we minimize the chances of over-scoring a letter. Figure 19-6 shows these four letters in reverse ETAOIN order.

Figure 19-6: The frequency match score will not increase if the four letters are in reverse ETAOIN order.
By arranging the letters in reverse ETAOIN order, we avoid artificially increasing the frequency match score through a chance ordering of I, N, V, and K. This is also true if there are eighteen letters with higher frequency counts and four letters with lower frequency counts, as shown in Figure 19-7.

Figure 19-7: Reversing ETAOIN order for less frequent letters also avoids increasing the match score.
The reverse sort order ensures that K and V don’t match any of the six least frequent letters in English and again avoids increasing the frequency match score by two points.
To sort each list value in the freqToLetter dictionary in reverse ETAOIN order, we’ll need to pass a method to Python’s sort() function. Let’s look at how to pass a function or method to another function.
On line 42, instead of calling the find() method, we pass find as a value to the sort() method call:
42. freqToLetter[freq].sort(key=ETAOIN.find, reverse=True)
We can do this because in Python, functions can be treated as values. In fact, defining a function named spam is the same as storing the function definition in a variable named spam. To see an example, enter the following code into the interactive shell:
>>> def spam():
... print('Hello!')
...
>>> spam()
Hello!
>>> eggs = spam
>>> eggs()
Hello!
In this example code, we define a function named spam() that prints the string 'Hello!'. This also means that the variable spam holds the function definition. Then we copy the function in the spam variable to the variable eggs. After doing so, we can call eggs() just like we can call spam()! Note that the assignment statement does not include parentheses after spam. If it did, it would instead call the spam() function and set the variable eggs to the return value that gets evaluated from the spam() function.
Since functions are values, we can pass them as arguments in function calls. Enter the following into the interactive shell to see an example:
>>> def doMath(func):
... return func(10, 5)
...
>>> def adding(a, b):
... return a + b
...
>>> def subtracting(a, b):
... return a - b
...
➊ >>> doMath(adding)
15
>>> doMath(subtracting)
5
Here we define three functions: doMath(), adding(), and subtracting(). When we pass the function in adding to the doMath() call ➊, we are assigning adding to the variable func, and func(10, 5) is calling adding() and passing 10 and 5 to it. So the call func(10, 5) is effectively the same as the call adding(10, 5). This is why doMath(adding) returns 15. Similarly, when we pass subtracting to the doMath() call, doMath(subtracting) returns 5 because func(10, 5) is the same as subtracting(10, 5).
Passing a function or method to the sort() method lets us implement different sorting behavior. Normally, sort() sorts the values in a list in alphabetical order:
>>> spam = ['C', 'B', 'A']
>>> spam.sort()
>>> spam
['A', 'B', 'C']
But if we pass a function (or method) for the key keyword argument, the values in the list are sorted by the function’s return value when each value in the list is passed to that function. For example, we can also pass the ETAOIN.find() string method as the key to a sort() call, as follows:
>>> ETAOIN = 'ETAOINSHRDLCUMWFGYPBVKJXQZ'
>>> spam.sort(key=ETAOIN.find)
>>> spam
['A', 'C', 'B']
When we pass ETAOIN.find to the sort() method, instead of sorting the strings in alphabetical order, the sort() method first calls the find() method on each string so that ETAOIN.find('A'), ETAOIN.find('B'), and ETAOIN.find('C') return the indexes 2, 19, and 11, respectively—each string’s position in the ETAOIN string. Then sort() uses these returned indexes, rather the original 'A', 'B', and 'C' strings, to sort the items in the spam list. This is why the 'A', 'B', and 'C' strings get sorted as 'A', 'C', and 'B', reflecting the order in which they appear in ETAOIN.
To sort letters in reverse ETAOIN order, we first need to sort them based on the ETAOIN string by assigning ETAOIN.find to key. After the method has been called on all the letters so that they’re all indexes, the sort() method sorts the letters based on their numerical index.
Usually, the sort() function sorts whatever list it’s called on in alphabetical or numerical order, which is known as ascending order. To sort items in descending order, which is in reverse alphabetical or reverse numerical order, we pass True for the sort() method’s reverse keyword argument.
We do all of this on line 42:
39. # Third, put each list of letters in reverse "ETAOIN" order, and then
40. # convert it to a string:
41. for freq in freqToLetter:
42. freqToLetter[freq].sort(key=ETAOIN.find, reverse=True)
43. freqToLetter[freq] = ''.join(freqToLetter[freq])
Recall that at this point, freqToLetter is a dictionary that stores integer frequency counts as its keys and lists of letter strings as its values. The letter strings at key freq are being sorted, not the freqToLetter dictionary itself. Dictionaries cannot be sorted because they have no order: there is no “first” or “last” key-value pair as there is for list items.
Using the """Alan Mathison Turing...""" example value for freqToLetter again, when the loop finishes, this would be the value stored in freqToLetter:
{1: 'Z', 2: 'QJ', 3: 'X', 135: 'A', 8: 'K', 139: 'I', 140: 'T', 14: 'V',
21: 'Y', 30: 'BW', 36: 'P', 37: 'FU', 39: 'G', 58: 'MD', 62: 'L', 196: 'E',
74: 'C', 87: 'H', 89: 'S', 106: 'R', 113: 'O', 122: 'N'}
Notice that the strings for the 30, 37, and 58 keys are all sorted in reverse ETAOIN order. Before the loop executed, the key-value pairs looked like this: {30: ['B', 'W'], 37: ['F', 'U'], 58: ['D', 'M'], ...}. After the loop, they should look like this: {30: 'BW', 37: 'FU', 58: 'MD', ...}.
The join() method call on line 43 changes the list of strings into a single string. For example, the value in freqToLetter[30] is ['B', 'W'], which is joined as 'BW'.
The fourth step of getFrequencyOrder() is to sort the strings from the freqToLetter dictionary by the frequency count and to convert the strings to a list. Keep in mind that because the key-value pairs in dictionaries are unordered, a list value of all the keys or values in a dictionary will be a list of items in random order. This means that we’ll also need to sort this list.
The keys(), values(), and items() dictionary methods each convert parts of a dictionary into a non-dictionary data type. After a dictionary is converted to another data type, it can be converted into a list using the list() function.
Enter the following into the interactive shell to see an example:
>>> spam = {'cats': 10, 'dogs': 3, 'mice': 3}
>>> spam.keys()
dict_keys(['mice', 'cats', 'dogs'])
>>> list(spam.keys())
['mice', 'cats', 'dogs']
>>> list(spam.values())
[3, 10, 3]
To get a list value of all the keys in a dictionary, we can use the keys() method to return a dict_keys object that we can then pass to the list() function. A similar dictionary method named values() returns a dict_values object. These examples give us a list of the dictionary’s keys and a list of its values, respectively.
To get both the keys and the values, we can use the items() dictionary method to return a dict_items object, which makes the key-value pairs into tuples. We can then pass the tuples to list(). Enter the following into the interactive shell to see this in action:
>>> spam = {'cats': 10, 'dogs': 3, 'mice': 3}
>>> list(spam.items())
[('mice', 3), ('cats', 10), ('dogs', 3)]
By calling items() and list(), we convert the spam dictionary’s key-value pairs into a list of tuples. This is exactly what we need to do with the freqToLetter dictionary so we can sort the letter strings in numerical order by frequency.
The freqToLetter dictionary has integer frequency counts as its keys and lists of single-letter strings as its values. To sort the strings in frequency order, we call the items() method and the list() function to create a list of tuples of the dictionary’s key-value pairs. Then we store this list of tuples in a variable named freqPairs on line 47:
45. # Fourth, convert the freqToLetter dictionary to a list of
46. # tuple pairs (key, value), and then sort them:
47. freqPairs = list(freqToLetter.items())
On line 48, we pass the getItemAtIndexZero function value that we defined earlier in the program to the sort() method call:
48. freqPairs.sort(key=getItemAtIndexZero, reverse=True)
The getItemAtIndexZero() function gets the first item in a tuple, which in this case is the frequency count integer. This means that the items in freqPairs are sorted by the numeric order of the frequency count integers. Line 48 also passes True for the reverse keyword argument so the tuples are reverse ordered from largest frequency count to smallest.
Continuing with the """Alan Mathison Turing...""" example, after line 48 executes, this would be the value of freqPairs:
[(196, 'E'), (140, 'T'), (139, 'I'), (135, 'A'), (122, 'N'), (113, 'O'),
(106, 'R'), (89, 'S'), (87, 'H'), (74, 'C'), (62, 'L'), (58, 'MD'), (39, 'G'),
(37, 'FU'), (36, 'P'), (30, 'BW'), (21, 'Y'), (14, 'V'), (8, 'K'), (3, 'X'),
(2, 'QJ'), (1, 'Z')]
The freqPairs variable is now a list of tuples ordered from the most frequent to least frequent letters: the first value in each tuple is an integer representing the frequency count, and the second value is a string containing the letters associated with that frequency count.
The fifth step of getFrequencyOrder() is to create a list of all the strings from the sorted list in freqPairs. We want to end up with a single string value whose letters are in the order of their frequency, so we don’t need the integer values in freqPairs. The variable freqOrder starts as a blank list on line 52, and the for loop on line 53 appends the string at index 1 of each tuple in freqPairs to the end of freqOrder:
50. # Fifth, now that the letters are ordered by frequency, extract all
51. # the letters for the final string:
52. freqOrder = []
53. for freqPair in freqPairs:
54. freqOrder.append(freqPair[1])
Continuing with the example, after line 53’s loop has finished, freqOrder should contain ['E', 'T', 'I', 'A', 'N', 'O', 'R', 'S', 'H', 'C', 'L', 'MD', 'G', 'FU', 'P', 'BW', 'Y', 'V', 'K', 'X', 'QJ', 'Z'] as its value.
Line 56 creates a string from the list of strings in freqOrder by joining them using the join() method:
56. return ''.join(freqOrder)
For the """Alan Mathison Turing...""" example, getFrequencyOrder() returns the string 'ETIANORSHCLMDGFUPBWYVKXQJZ'. According to this ordering, E is the most frequent letter in the example string, T is the second most frequent letter, I is the third most frequent, and so on.
Now that we have the letter frequency of the message as a string value, we can compare it to the string value of English’s letter frequency ('ETAOINSHRDLCUMWFGYPBVKJXQZ') to see how closely they match.
The englishFreqMatchScore() function takes a string for message and then returns an integer between 0 and 12 representing the string’s frequency match score. The higher the score, the more closely the letter frequency in message matches the frequency of normal English text.
59. def englishFreqMatchScore(message):
60. # Return the number of matches that the string in the message
61. # parameter has when its letter frequency is compared to English
62. # letter frequency. A "match" is how many of its six most frequent
63. # and six least frequent letters are among the six most frequent and
64. # six least frequent letters for English.
65. freqOrder = getFrequencyOrder(message)
The first step in calculating the frequency match score is to get the letter frequency ordering of message by calling the getFrequencyOrder() function, which we do on line 65. We store the ordered string in the variable freqOrder.
The matchScore variable starts at 0 on line 67 and is incremented by the for loop beginning on line 69, which compares the first six letters of the ETAOIN string and the first six letters of freqOrder, giving a point for each letter they have in common:
67. matchScore = 0
68. # Find how many matches for the six most common letters there are:
69. for commonLetter in ETAOIN[:6]:
70. if commonLetter in freqOrder[:6]:
71. matchScore += 1
Recall that the [:6] slice is the same as [0:6], so lines 69 and 70 slice the first six letters of the ETAOIN and freqOrder strings, respectively. If any of the letters E, T, A, O, I, or N is also in the first six letters in the freqOrder string, the condition on line 70 is True, and line 71 increments matchScore.
Lines 73 to 75 are similar to lines 69 to 71, except in this case they check whether the last six letters in the ETAOIN string (V, K, J, X, Q, and Z) are in the last six letters in the freqOrder string. If they are, matchScore is incremented.
72. # Find how many matches for the six least common letters there are:
73. for uncommonLetter in ETAOIN[-6:]:
74. if uncommonLetter in freqOrder[-6:]:
75. matchScore += 1
Line 77 returns the integer in matchScore:
77. return matchScore
We ignore the 14 letters in the middle of the frequency order when calculating the frequency match score. The frequencies of these middle letters are too similar to each other to give meaningful information.
In this chapter, you learned how to use the sort() function to sort list values in alphabetical or numerical order and how to use the reverse and key keyword arguments to sort list values in different ways. You learned how to convert dictionaries to lists using the keys(), values(), and items() dictionary methods. You also learned that you can pass functions as values in function calls.
In Chapter 20, we’ll use the frequency analysis module we wrote in this chapter to hack the Vigenère cipher!