







Use this link to get 70% off the Automate the Boring Stuff online video course.
Support me on Patreon








“Weakening encryption or creating backdoors to encrypted devices and data for use by the good guys would actually create vulnerabilities to be exploited by the bad guys.”
—Tim Cook, CEO of Apple, 2015

Unlike the Caesar cipher, the decryption process for the transposition cipher is different from the encryption process. In this chapter, you’ll create a separate program named transpositionDecrypt.py to handle decryption.
Pretend you’ve sent the ciphertext “Cenoonommstmme oo snnio. s s c” to a friend (and they already know that the secret key is 8). The first step for them to decrypt the ciphertext is to calculate the number of boxes they need to draw. To determine this number, they must divide the length of the ciphertext message by the key and round up to the nearest whole number if the result isn’t already a whole number. The length of the ciphertext is 30 characters (the same as the plaintext) and the key is 8, so 30 divided by 8 is 3.75.

Figure 8-1: Decrypting the message by reversing the grid
Rounding up 3.75 to 4, your friend will draw a grid of boxes with four columns (the number they just calculated) and eight rows (the key).
Your friend also needs to calculate the number of boxes to shade in. Using the total number of boxes (32), they subtract the length of the ciphertext (which is 30): 32 – 30 = 2. They shade in the bottom two boxes in the rightmost column.
Then they start filling in the boxes, placing one character of the ciphertext in each box. Starting at the top left, they fill in toward the right, as you did when you were encrypting. The ciphertext is “Cenoonommstmme oo snnio. s s c”, so “Ceno” goes in the first row, “onom” goes in the second row, and so on. When they’re done, the boxes will look like Figure 8-1 (a ▪ represents a space).
Your friend who received the ciphertext notices that when they read the text going down the columns, the original plaintext is restored: “Common sense is not so common.”
To recap, the steps for decrypting are as follows:
Calculate the number of columns you need by dividing the length of the message by the key and then rounding up.
Draw boxes in columns and rows. Use the number of columns you calculated in step 1. The number of rows is the same as the key.
Calculate the number of boxes to shade in by taking the total number of boxes (the number of rows multiplied by the number of columns) and subtracting the length of the ciphertext message.
Shade in the number of boxes you calculated in step 3 at the bottom of the rightmost column.
Fill in the characters of the ciphertext starting at the top row and going from left to right. Skip any of the shaded boxes.
Get the plaintext by reading the leftmost column from top to bottom, and continuing to do the same in each column.
Note that if you used a different key, you’d draw the wrong number of rows. Even if you followed the other steps in the decryption process correctly, the plaintext would be random garbage (similar to if you used the wrong key with the Caesar cipher).
Open a new file editor window by clicking File▸New File. Enter the following code into the file editor and then save it as transpositionDecrypt.py. Remember to place pyperclip.py in the same directory. Press F5 to run the program.
transposition
Decrypt.py
1. # Transposition Cipher Decryption
2. # https://www.nostarch.com/crackingcodes/ (BSD Licensed)
3.
4. import math, pyperclip
5.
6. def main():
7. myMessage = 'Cenoonommstmme oo snnio. s s c'
8. myKey = 8
9.
10. plaintext = decryptMessage(myKey, myMessage)
11.
12. # Print with a | (called "pipe" character) after it in case
13. # there are spaces at the end of the decrypted message:
14. print(plaintext + '|')
15.
16. pyperclip.copy(plaintext)
17.
18.
19. def decryptMessage(key, message):
20. # The transposition decrypt function will simulate the "columns" and
21. # "rows" of the grid that the plaintext is written on by using a list
22. # of strings. First, we need to calculate a few values.
23.
24. # The number of "columns" in our transposition grid:
25. numOfColumns = int(math.ceil(len(message) / float(key)))
26. # The number of "rows" in our grid:
27. numOfRows = key
28. # The number of "shaded boxes" in the last "column" of the grid:
29. numOfShadedBoxes = (numOfColumns * numOfRows) - len(message)
30.
31. # Each string in plaintext represents a column in the grid:
32. plaintext = [''] * numOfColumns
33.
34. # The column and row variables point to where in the grid the next
35. # character in the encrypted message will go:
36. column = 0
37. row = 0
38.
39. for symbol in message:
40. plaintext[column] += symbol
41. column += 1 # Point to the next column.
42.
43. # If there are no more columns OR we're at a shaded box, go back
44. # to the first column and the next row:
45. if (column == numOfColumns) or (column == numOfColumns - 1 and
row >= numOfRows - numOfShadedBoxes):
46. column = 0
47. row += 1
48.
49. return ''.join(plaintext)
50.
51.
52. # If transpositionDecrypt.py is run (instead of imported as a module),
53. # call the main() function:
54. if __name__ == '__main__':
55. main()
When you run the transpositionDecrypt.py program, it produces this output:
Common sense is not so common.|
If you want to decrypt a different message or use a different key, change the value assigned to the myMessage and myKey variables on lines 7 and 8.
The first part of the transpositionDecrypt.py program is similar to the first part of transpositionEncrypt.py:
1. # Transposition Cipher Decryption
2. # https://www.nostarch.com/crackingcodes/ (BSD Licensed)
3.
4. import math, pyperclip
5.
6. def main():
7. myMessage = 'Cenoonommstmme oo snnio. s s c'
8. myKey = 8
9.
10. plaintext = decryptMessage(myKey, myMessage)
11.
12. # Print with a | (called "pipe" character) after it in case
13. # there are spaces at the end of the decrypted message:
14. print(plaintext + '|')
15.
16. pyperclip.copy(plaintext)
The pyperclip module is imported along with another module named math on line 4. If you separate the module names with commas, you can import multiple modules with one import statement.
The main() function, which we start defining on line 6, creates variables named myMessage and myKey and then calls the decryption function decryptMessage(). The return value of decryptMessage() is the decrypted plaintext of the ciphertext and key. This is stored in a variable named plaintext, which is printed to the screen (with a pipe character at the end in case there are spaces at the end of the message) and then copied to the clipboard.
The decryptMessage() function follows the six decrypting steps described on page 100 and then returns the results of decryption as a string. To make decryption easier, we’ll use functions from the math module, which we imported earlier in the program.
Python’s round() function will round a floating-point number (a number with a decimal point) to the closest integer. The math.ceil() and math.floor() functions (in Python’s math module) will round a number up and down, respectively.
When you divide numbers using the / operator, the expression returns a floating-point number (a number with a decimal point). This happens even if the number divides evenly. For example, enter the following into the interactive shell:
>>> 21 / 7
3.0
>>> 22 / 5
4.4
If you want to round a number to the nearest integer, you can use the round() function. To see how the function works, enter the following:
>>> round(4.2)
4
>>> round(4.9)
5
>>> round(5.0)
5
>>> round(22 / 5)
4
If you only want to round up, you need to use the math.ceil() function, which represents “ceiling.” If you only want to round down, use math.floor(). These functions exist in the math module, which you need to import before calling them. Enter the following into the interactive shell:
>>> import math
>>> math.floor(4.0)
4
>>> math.floor(4.2)
4
>>> math.floor(4.9)
4
>>> math.ceil(4.0)
4
>>> math.ceil(4.2)
5
>>> math.ceil(4.9)
5
The math.floor() function will always remove the decimal point from the float and convert it to an integer to round down, and math.ceil() will instead increment the ones place of the float and convert it to an integer to round up.
The decryptMessage() function implements each of the decryption steps as Python code. It takes an integer key and a message string as arguments. The math.ceil() function is used for the transposition decryption in decryptMessage() when the columns are calculated to determine the number of boxes that need to be made:
19. def decryptMessage(key, message):
20. # The transposition decrypt function will simulate the "columns" and
21. # "rows" of the grid that the plaintext is written on by using a list
22. # of strings. First, we need to calculate a few values.
23.
24. # The number of "columns" in our transposition grid:
25. numOfColumns = int(math.ceil(len(message) / float(key)))
26. # The number of "rows" in our grid:
27. numOfRows = key
28. # The number of "shaded boxes" in the last "column" of the grid:
29. numOfShadedBoxes = (numOfColumns * numOfRows) - len(message)
Line 25 calculates the number of columns by dividing len(message) by the integer in key. This value is passed to the math.ceil() function, and that return value is stored in numOfColumns. To make this program compatible with Python 2, we call float() so the key becomes a floating-point value. In Python 2, the result of dividing two integers is automatically rounded down. Calling float() avoids this behavior without affecting the behavior under Python 3.
Line 27 calculates the number of rows, which is the integer stored in key. This value gets stored in the variable numOfRows.
Line 29 calculates the number of shaded boxes in the grid, which is the number of columns times rows, minus the length of the message.
If you’re decrypting “Cenoonommstmme oo snnio. s s c” with a key of 8, numOfColumns is set to 4, numOfRows is set to 8, and numOfShadedBoxes is set to 2.
Just like the encryption program had a variable named ciphertext that was a list of strings to represent the grid of ciphertext, decryptMessage() also has a list-of-strings variable named plaintext:
31. # Each string in plaintext represents a column in the grid:
32. plaintext = [''] * numOfColumns
These strings are blank at first, with one string for each column of the grid. Using list replication, you can multiply a list of one blank string by numOfColumns to make a list of several blank strings equal to the number of columns needed.
Keep in mind that this plaintext is different from the plaintext in the main() function. Because the decryptMessage() function and the main() function each has its own local scope, the functions’ plaintext variables are different and just happen to have the same name.
Remember that the grid for the 'Cenoonommstmme oo snnio. s s c' example looks like Figure 8-1 on page 100.
The plaintext variable will have a list of strings, and each string in the list will be a single column of this grid. For this decryption, you want plaintext to end up with the following value:
['Common s', 'ense is ', 'not so c', 'ommon.']
That way, you can join all the list’s strings together to return the 'Common sense is not so common.' string value.
To make the list, we first need to place each symbol in message in the correct string inside the plaintext list one at a time. We’ll create two variables named column and row to track the column and row where the next character in message should go; these variables should start at 0 to begin at the first column and first row. Lines 36 and 37 do this:
34. # The column and row variables point to where in the grid the next
35. # character in the encrypted message will go:
36. column = 0
37. row = 0
Line 39 starts a for loop that iterates over the characters in the message string. Inside this loop, the code will adjust the column and row variables so it concatenates symbol to the correct string in the plaintext list:
39. for symbol in message:
40. plaintext[column] += symbol
41. column += 1 # Point to the next column.
Line 40 concatenates symbol to the string at index column in the plaintext list, because each string in plaintext represents a column. Then line 41 adds 1 to column (that is, it increments column) so that on the next iteration of the loop, symbol will be concatenated to the next string in the plaintext list.
We’ve handled incrementing column and row, but we’ll also need to reset the variables to 0 in some cases. To understand the code that does that, you’ll need to understand Boolean operators.
Boolean operators compare Boolean values (or expressions that evaluate to a Boolean value) and evaluate to a Boolean value. The Boolean operators and and or can help you form more complicated conditions for if and while statements. The and operator connects two expressions and evaluates to True if both expressions evaluate to True. The or operator connects two expressions and evaluates to True if one or both expressions evaluate to True; otherwise, these expressions evaluate to False. Enter the following into the interactive shell to see how the and operator works:
>>> 10 > 5 and 2 < 4
True
>>> 10 > 5 and 4 != 4
False
The first expression evaluates to True because the expressions on either side of the and operator both evaluate to True. In other words, the expression 10 > 5 and 2 < 4 evaluates to True and True, which in turn evaluates to True.
However, in the second expression, although 10 > 5 evaluates to True, the expression 4 != 4 evaluates to False. This means the expression evaluates to True and False. Because both expressions have to be True for the and operator to evaluate to True, the whole expression evaluates to False.
If you ever forget how a Boolean operator works, you can look at its truth table, which shows what different combinations of Boolean values evaluate to based on the operator used. Table 8-1 is a truth table for the and operator.
Table 8-1: The and Operator Truth Table
A and B |
Evaluates to |
True and True |
True |
True and False |
False |
False and True |
False |
False and False |
False |
To see how the or operator works, enter the following into the interactive shell:
>>> 10 > 5 or 4 != 4
True
>>> 10 < 5 or 4 != 4
False
When you’re using the or operator, only one side of the expression must be True for the or operator to evaluate the whole expression as True, which is why 10 > 5 or 4 != 4 evaluates to True. However, because both the expression 10 < 5 and the expression 4 != 4 are False, the second expression evaluates to False or False, which in turn evaluates to False.
The or operator’s truth table is shown in Table 8-2.
Table 8-2: The or Operator Truth Table
A or B |
Evaluates to |
True or True |
True |
True or False |
True |
False or True |
True |
False or False |
False |
The third Boolean operator is not. The not operator evaluates to the opposite Boolean value of the value it operates on. So not True is False and not False is True. Enter the following into the interactive shell:
>>> not 10 > 5
False
>>> not 10 < 5
True
>>> not False
True
>>> not not False
False
>>> not not not not not False
True
As you can see in the last two expressions, you can even use multiple not operators. The not operator’s truth table is shown in Table 8-3.
Table 8-3: The not Operator Truth Table
not A |
Evaluates to |
not True |
False |
not False |
True |
Similar to how for loops let you do the same task as while loops but with less code, the and and or operators also let you shorten your code. Enter the following two pieces of code, which have the same result, into the interactive shell:
>>> if 10 > 5:
... if 2 < 4:
... print('Hello!')
...
Hello!
>>> if 10 > 5 and 2 < 4:
... print('Hello!')
...
Hello!
The and operator can take the place of two if statements that check each part of the expression separately (where the second if statement is inside the first if statement’s block).
You can also replace an if and elif statement with the or operator. To give this a try, enter the following into the interactive shell:
>>> if 4 != 4:
... print('Hello!')
... elif 10 > 5:
... print('Hello!')
...
Hello!
>>> if 4 != 4 or 10 > 5:
... print('Hello!')
...
Hello!
The if and elif statements will each check a different part of the expression, whereas the or operator can check both statements in one line.
You know that math operators have an order of operations, and so do the and, or, and not operators. First, not is evaluated, then and, and then or. Enter the following into the interactive shell:
>>> not False and False # not False evaluates first
False
>>> not (False and False) # (False and False) evaluates first
True
In the first line of code, not False is evaluated first, so the expression becomes True and False, which evaluates to False. In the second line, parentheses are evaluated first, even before the not operator, so False and False is evaluated as False, and the expression becomes not (False), which is True.
Now that you know how Boolean operators work, you can learn how the column and row variables are reset in transpositionDecrypt.py.
There are two cases in which you’ll want to reset column to 0 so that on the next iteration of the loop, symbol is added to the first string in the list in plaintext. In the first case, you want to do this if column is incremented past the last index in plaintext. In this situation, the value in column will be equal to numOfColumns. (Remember that the last index in plaintext will be numOfColumns minus one. So when column is equal to numOfColumns, it’s already past the last index.)
The second case is if column is at the last index and the row variable is pointing to a row that has a shaded box in the last column. As a visual example of that, the decryption grid with the column indexes along the top and the row indexes down the side is shown in Figure 8-2.
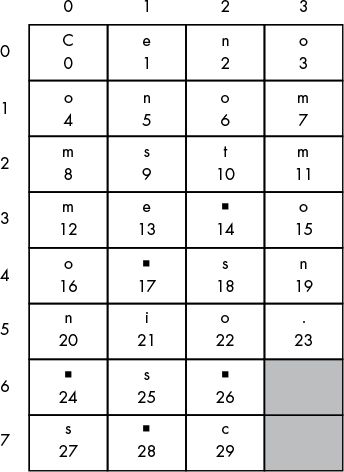
Figure 8-2: Decryption grid with column and row indexes
You can see that the shaded boxes are in the last column (whose index will be numOfColumns - 1) in rows 6 and 7. To calculate which row indexes potentially have shaded boxes, use the expression row >= numOfRows - numOfShadedBoxes. In our example with eight rows (with indexes 0 to 7), rows 6 and 7 are shaded. The number of unshaded boxes is the total number of rows (in our example, 8) minus the number of shaded boxes (in our example, 2). If the current row is equal to or greater than this number (8 – 2 = 6), we can know we have a shaded box. If this expression is True and column is also equal to numOfColumns - 1, then Python has encountered a shaded box; at this point, you want to reset column to 0 for the next iteration:
43. # If there are no more columns OR we're at a shaded box, go back
44. # to the first column and the next row:
45. if (column == numOfColumns) or (column == numOfColumns - 1 and
row >= numOfRows - numOfShadedBoxes):
46. column = 0
47. row += 1
These two cases are why the condition on line 45 is (column == numOfColumns) or (column == numOfColumns - 1 and row >= numOfRows - numOfShadedBoxes). Although that looks like a big, complicated expression, remember that you can break it down into smaller parts. The expression (column == numOfColumns) checks whether the column variable is past the index range, and the second part of the expression checks whether we’re at a column and row index that is a shaded box. If either of these two expressions is true, the block of code that executes will reset column to the first column by setting it to 0. You’ll also increment the row variable.
By the time the for loop on line 39 has finished looping over every character in message, the plaintext list’s strings have been modified so they’re now in the decrypted order (if the correct key was used). The strings in the plaintext list are joined together (with a blank string between each string) by the join() string method on line 49:
49. return ''.join(plaintext)
Line 49 also returns the string that the decryptMessage() function returns.
For decryption, plaintext will be ['Common s', 'ense is ', 'not so c', 'ommon.'], so ''.join(plaintext) will evaluate to 'Common sense is not so common.'
The first line that our program runs after importing modules and executing the def statements is the if statement on line 54.
52. # If transpositionDecrypt.py is run (instead of imported as a module),
53. # call the main() function:
54. if __name__ == '__main__':
55. main()
As with the transposition encryption program, Python checks whether this program has been run (instead of imported by a different program) by checking whether the __name__ variable is set to the string value '__main__'. If so, the code executes the main() function.
That’s it for the decryption program. Most of the program is in the decryptMessage() function. The programs we’ve written can encrypt and decrypt the message “Common sense is not so common.” with the key 8; however, you should try several other messages and keys to check that a message that is encrypted and then decrypted results in the same original message. If you don’t get the results you expect, you’ll know that either the encryption code or the decryption code doesn’t work. In Chapter 9, we’ll automate this process by writing a program to test our programs.
If you’d like to see a step-by-step trace of the transposition cipher decryption program’s execution, visit https://www.nostarch.com/crackingcodes/.