Fractal Art Maker for Python Turtle.py
Posted by Al Sweigart in misc
Fractals are beautiful, self-similar patterns that can be created by a computer from very simple rules. My Fractal Art Maker package makes it easy to use Python's turtle.py package to draw your own. You don't need to know recursion, but you can read my free book, The Recursive Book of Recursion if you're curious. If you want to learn how to draw pictures with Python code, I also have The Simple Turtle Tutorial.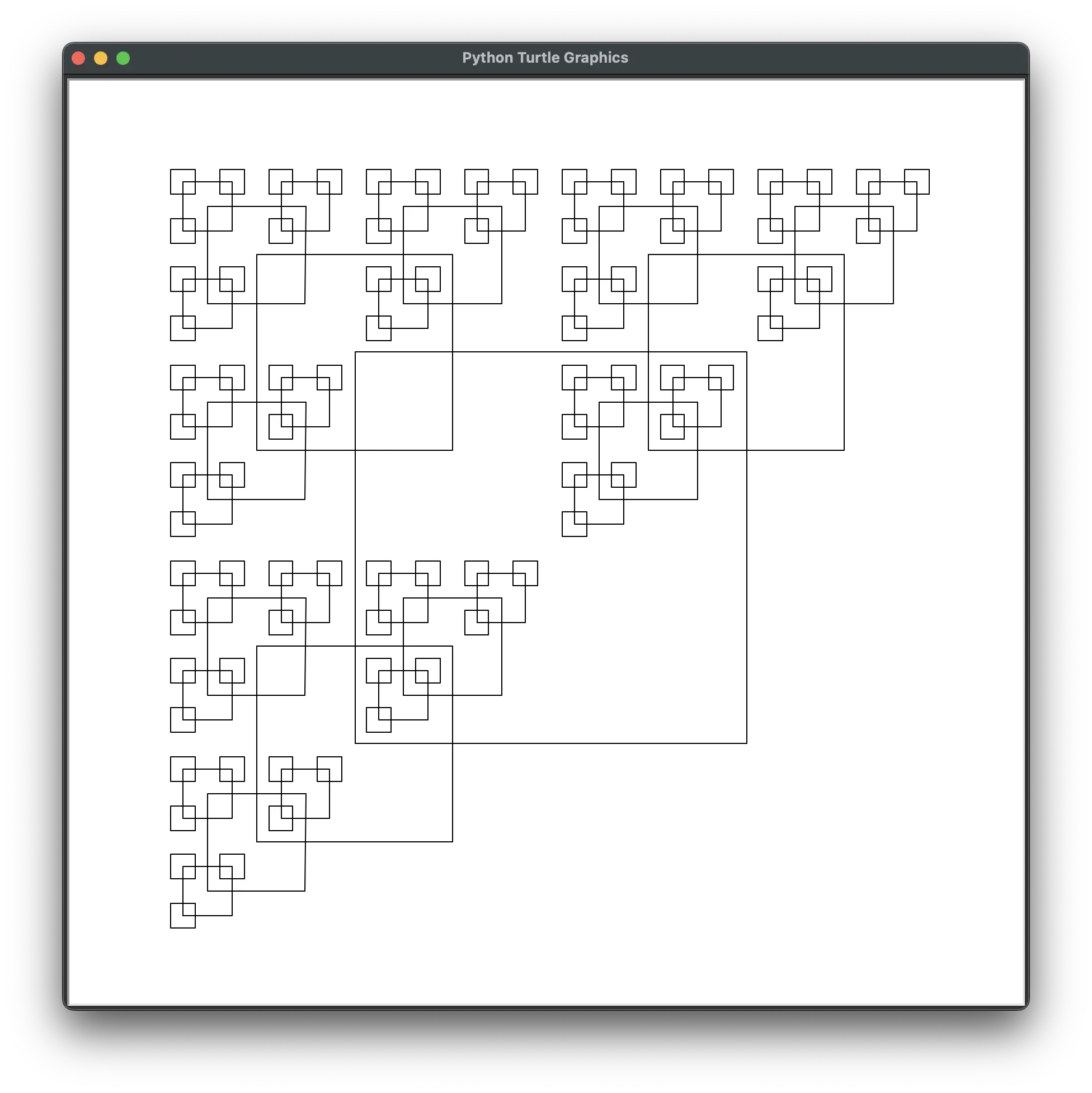
Installation and Quick Start
The package and documentation is hosted on PyPI and the git repo is also available. You can install it by running pip install fractalartmaker on Windows or pip3 install fractalartmaker on macOS/Linux. You can try this code out in the interactive shell:
import fractalartmaker as fam
fam.draw_fractal(my_square_drawing_function, 100, [{'size': 0.96, 'y': 0.5, 'angle': 11}], max_depth=50)
If you run the package as a module by running python3 -m fractalartmaker, you'll see several demo fractals.
How to Draw Fractals with FAM
The main function we'll use in the fam module is fam.draw_fractal(). We'll need to pass it a drawing function, which is a function that takes a size argument and draws a simple shape. Here's the code for square() function that draws a square:
def my_square_drawing_function(size):
# Move to the top-right corner before drawing:
turtle.penup()
turtle.forward(size // 2)
turtle.left(90)
turtle.forward(size // 2)
turtle.left(180)
turtle.pendown()
# Draw a square with sides of length `size`:
for i in range(4): # Draw four lines.
turtle.forward(size)
turtle.right(90)
On its own, this function will just draw a square of a given size. (Note that this function isn't recursive; it just draws one square.) But the fam.draw_fractal() function can use functions like this to create fractals.
To make a fractal, call fam.draw_fractal() and pass it this drawing function, a starting size (let's go with 100), and a list of recursion specification dictionaries. By recursion specification dictionary, I mean a list of dictionaries with (optional) keys 'size', 'x', 'y', and 'angle'. I'll explain what these keys do later, but try calling this:
fam.draw_fractal(my_square_drawing_function, 100, [{'size': 0.96, 'y': 0.5, 'angle': 11}])
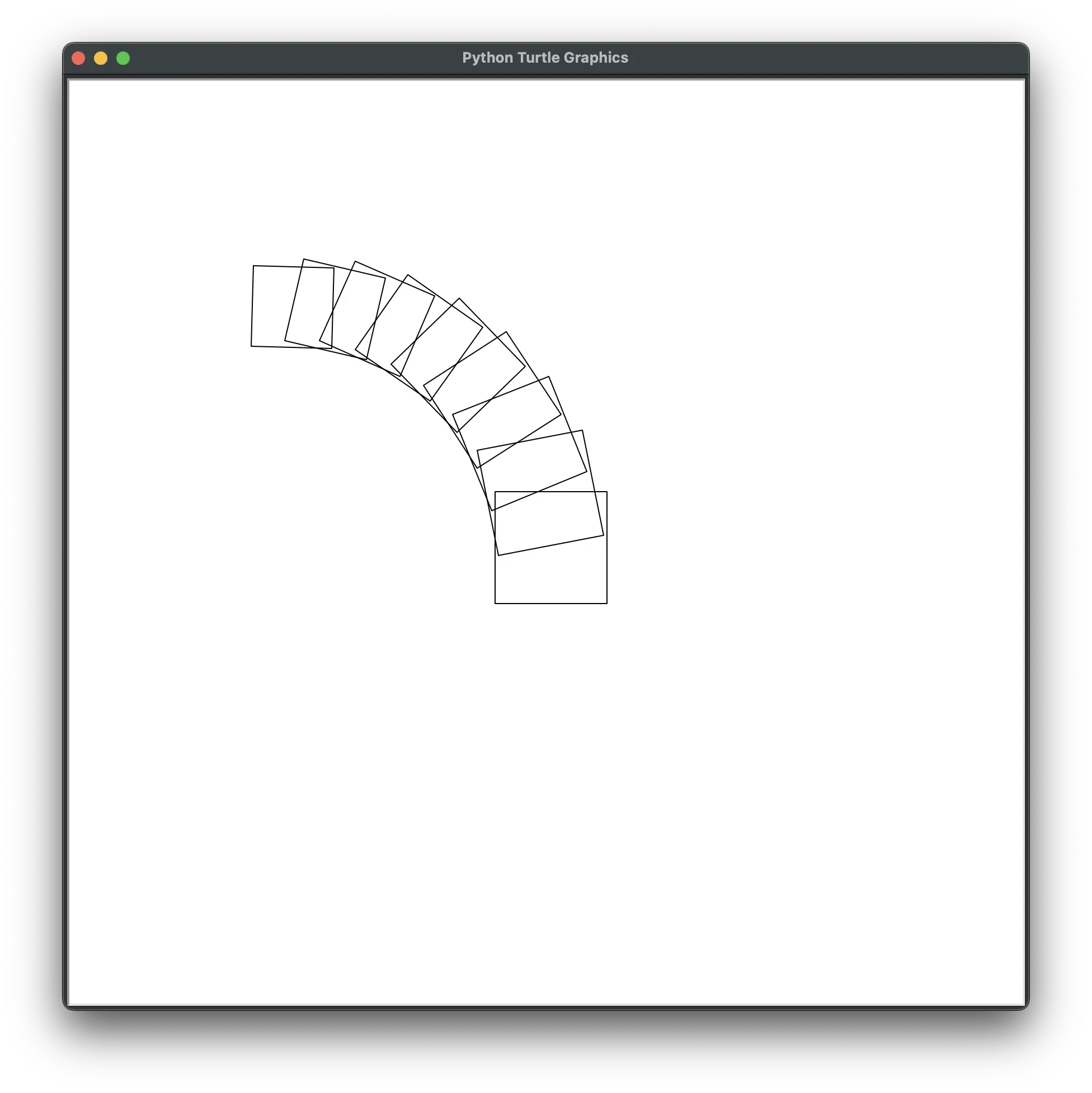
This draws a fractal similar to the fam.demo_horn() fractal. The 100 is the initial size for the first square to draw. The list of recursion specification dictionaries [{'size': 0.96, 'y': 0.5, 'angle': 11}] has one dictionary in it. This means for each shape drawn with the drawing function, we will draw one more recursive shape. The new square is drawn at 96% the original size (because the 'size' key is 0.96), located 50% of the size above the square (because the 'y' key is 0.5), after rotating it counterclockwise by 11 degrees (because the 'angle' is set to 11).
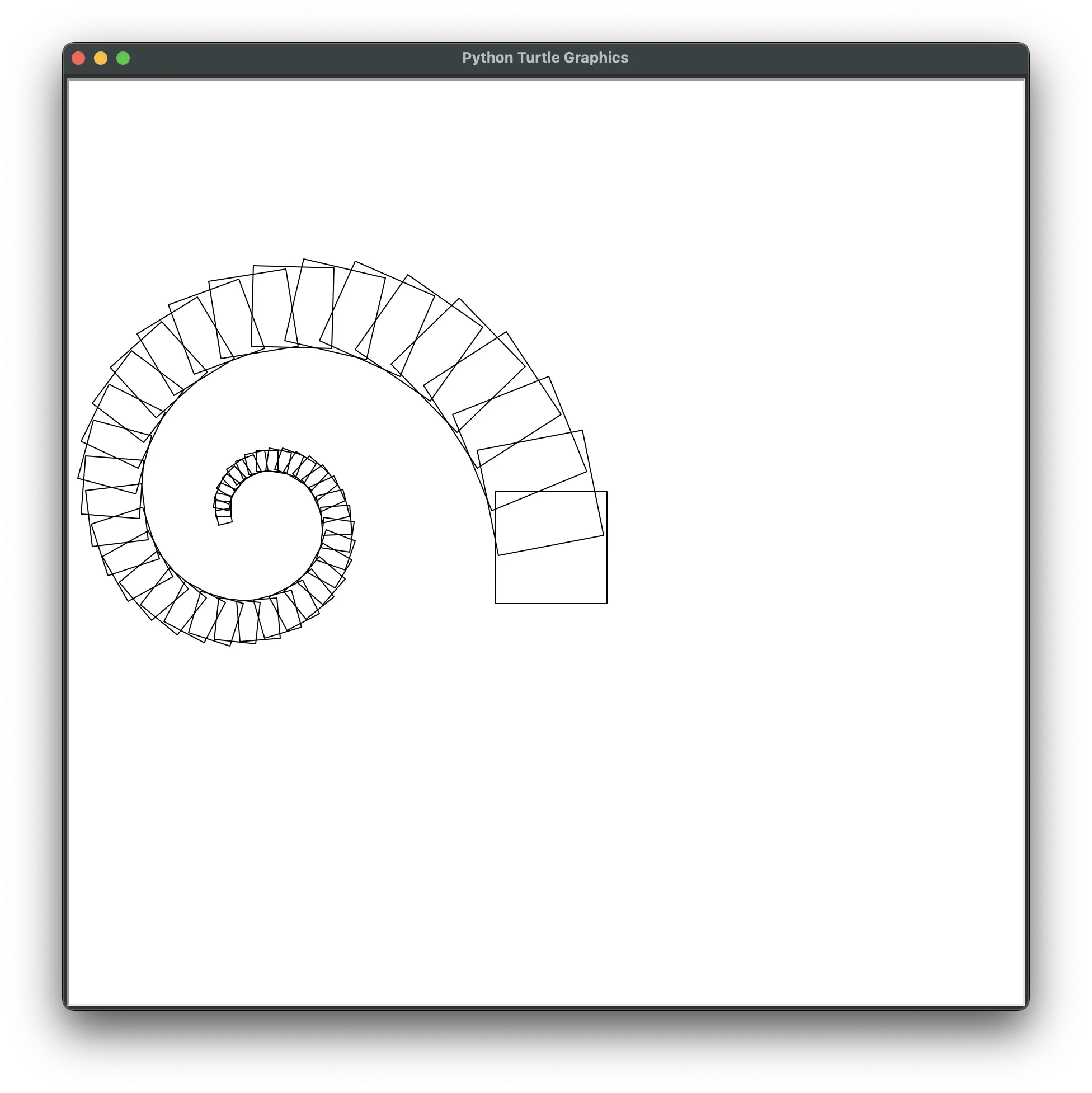
By default, fam.draw_fractal() only goes 8 recursive levels deep. You can change this by passing a max_depth argument.
fam.draw_fractal(my_square_drawing_function, 100, [{'size': 0.96, 'y': 0.5, 'angle': 11}], max_depth=50)
Let's make each square draw two squares by putting a second recursion specification dictionary in the list. Because each square will draw two squares (and both of those two squares will draw two squares each, and so on and so on), be sure to set max_depth to something small like it's default 8. Otherwise, the exponentially large amount of drawing will slow your program down to a crawl.
Let's make the second recursion specification dictionary the same as the first, but it's 'angle' key is -11 instead of 11. This will make it veer off clockwise by 11 degrees instead of the normal counterclockwise:
fam.draw_fractal(my_square_drawing_function, 100, [{'size': 0.96, 'y': 0.5, 'angle': 11}, {'size': 0.96, 'y': 0.5, 'angle': -11}], max_depth=8)
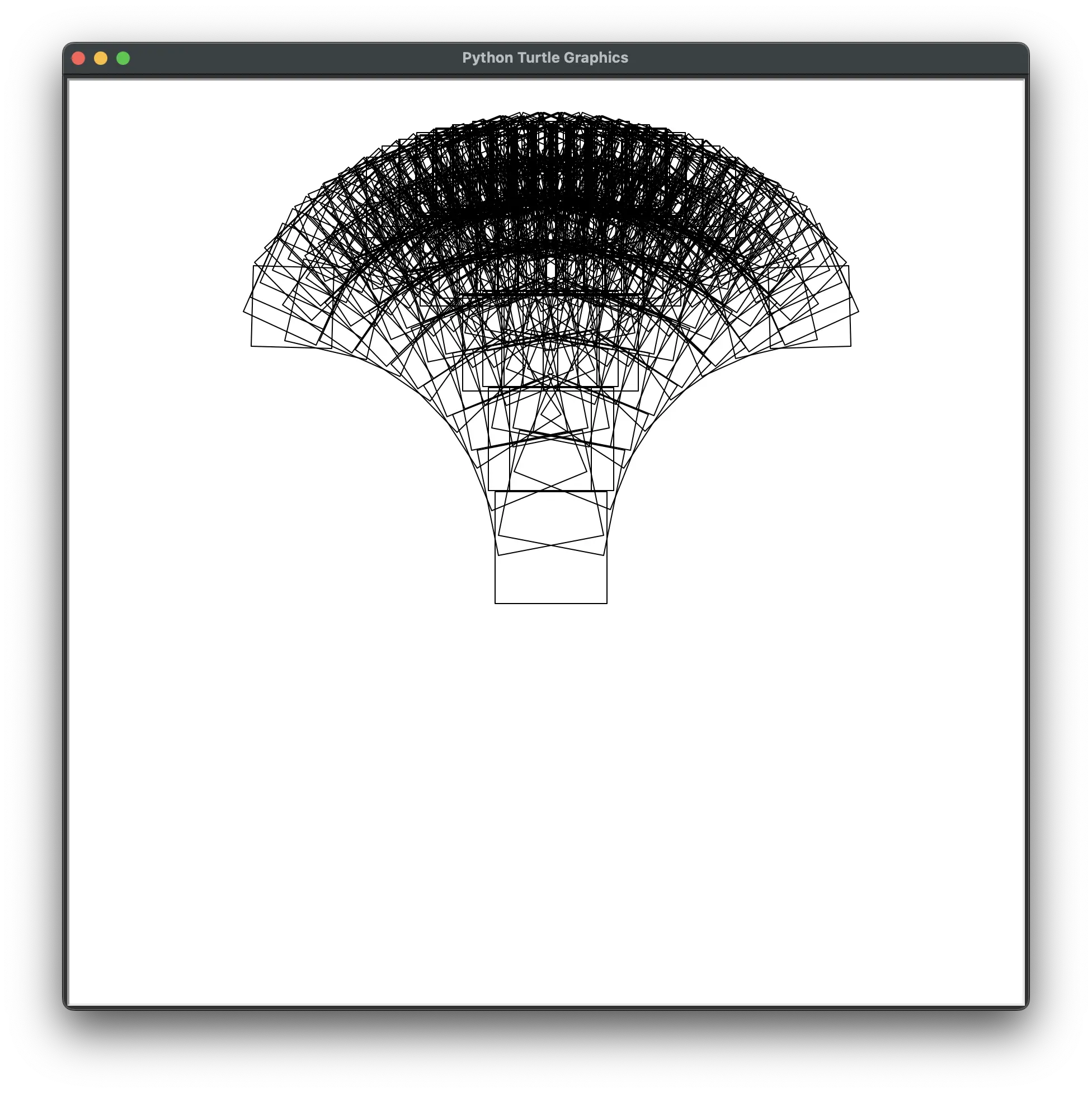
As you can see, it doesn't take much to fill up the window with too many shapes. The key to making aesthetically pleasing fractals is to take a light touch and spend a lot of time experimenting. For example, we could pass a list of three recursion specification dictionaries to draw squares in three of the corners of the parent square:
fam.draw_fractal(my_square_drawing_function, 350,
[{'size': 0.5, 'x': -0.5, 'y': 0.5},
{'size': 0.5, 'x': 0.5, 'y': 0.5},
{'size': 0.5, 'x': -0.5, 'y': -0.5}], max_depth=4)
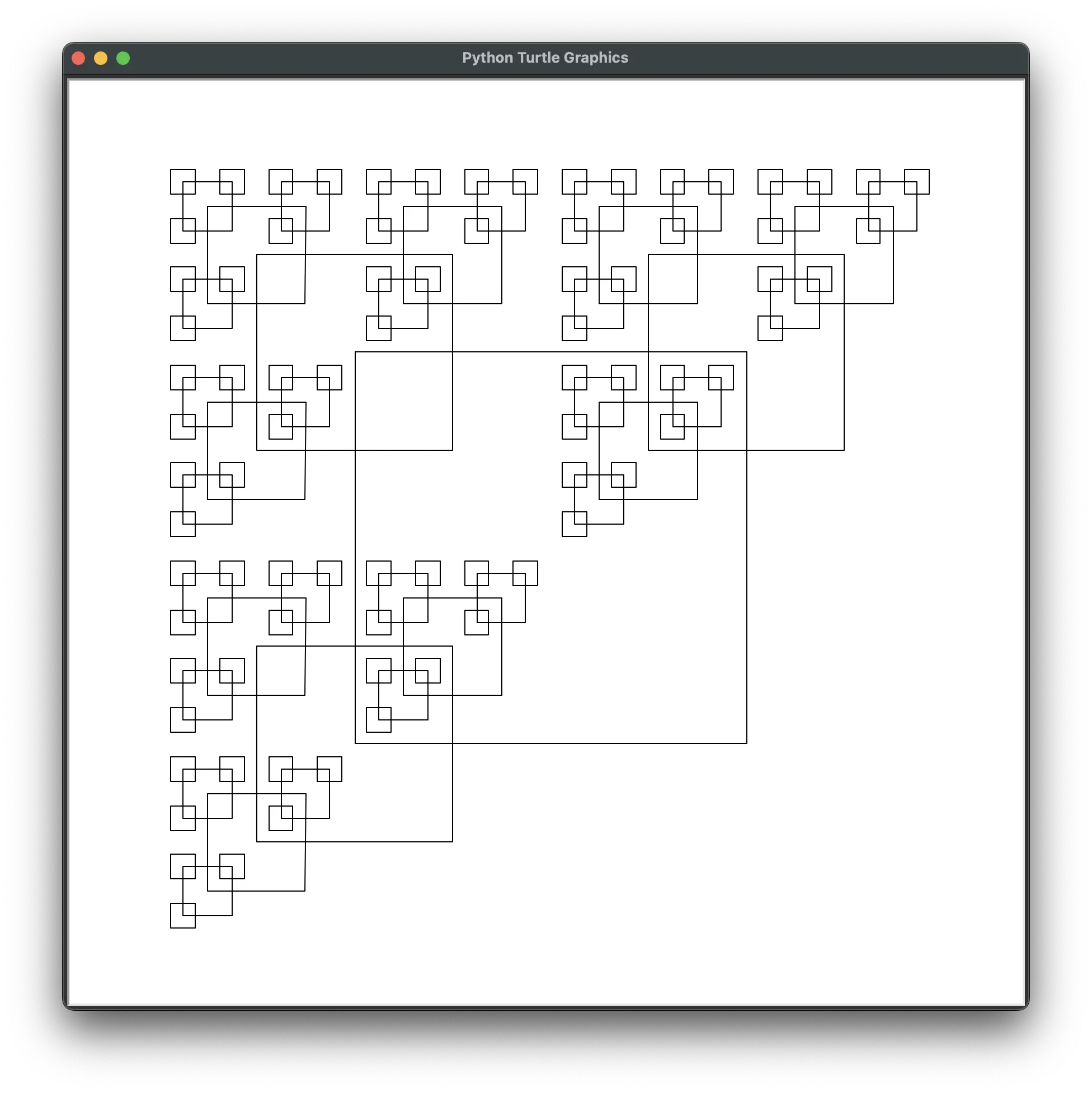
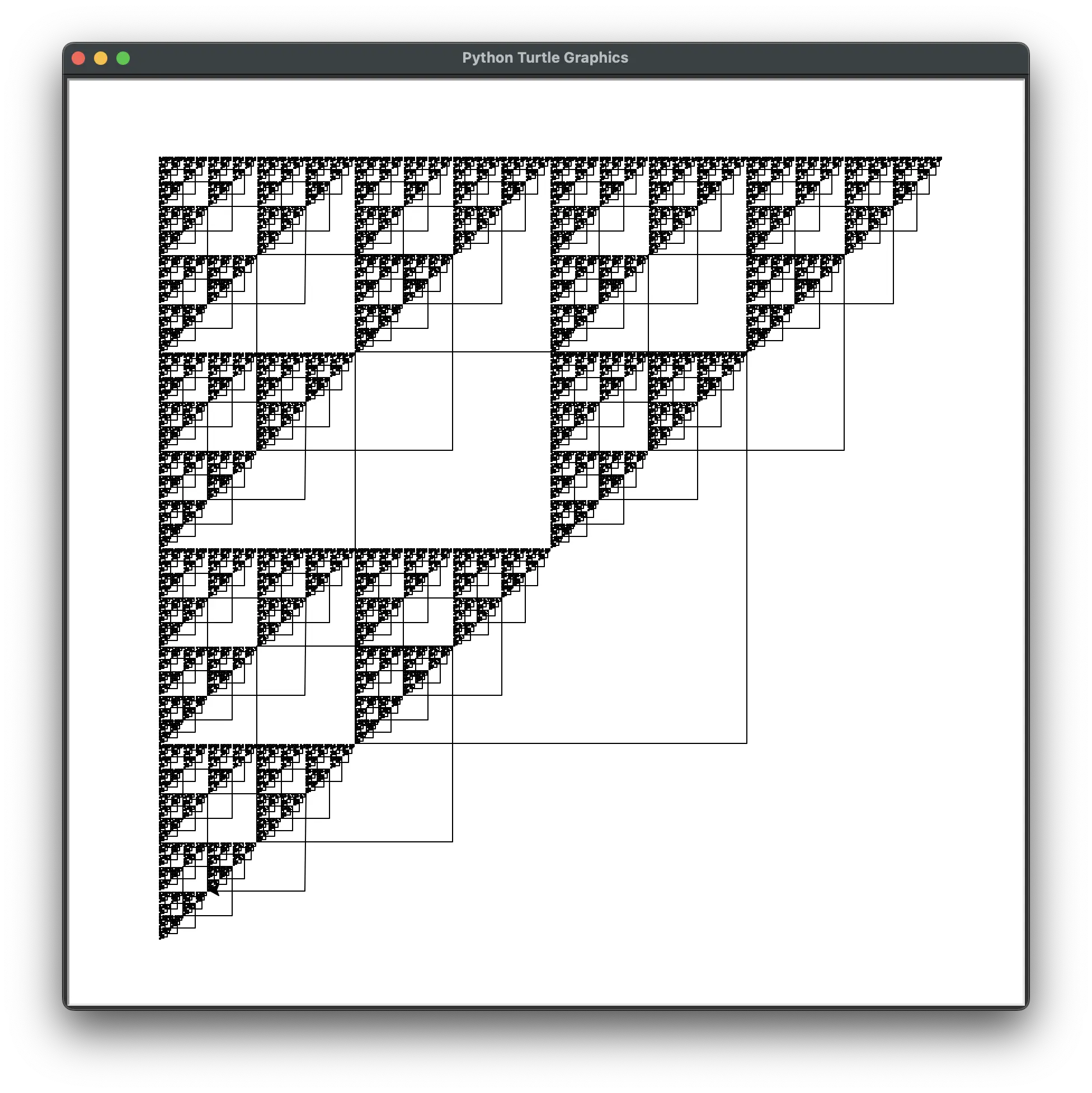
If we increase the max depth to 10, we can see a new pattern emerge:
fam.draw_fractal(my_square_drawing_function, 350,
[{'size': 0.5, 'x': -0.5, 'y': 0.5},
{'size': 0.5, 'x': 0.5, 'y': 0.5},
{'size': 0.5, 'x': -0.5, 'y': -0.5}], max_depth=10)
The fractalartmaker module comes with a fam.square and fam.triangle drawing functions that you can play with. Also take a look at the code for the demo functions inside the __init__.py file for more ideas. Check out the rest of this documentation for advanced tips. Good luck!
NOTE: Calling fam.draw_fractal() automatically calls turtle.reset() to clear the window and move the turtle cursor back to 0, 0. If you don't want this behavior, pass reset=False to fam.draw_fractal()
NOTE: To free you from having to import the turtle module yourself, you can call most turtle functions from the fam module: fam.reset(), fam.update(), and so on.
Gallery of Demo Fractals
def demo_four_corners(size=350, max_depth=5, **kwargs):
# Four Corners:
if 'colors' not in kwargs:
kwargs['colors'] = (('black', 'white'), ('black', 'gray'))
draw_fractal(square, size,
[{'size': 0.5, 'x': -0.5, 'y': 0.5},
{'size': 0.5, 'x': 0.5, 'y': 0.5},
{'size': 0.5, 'x': -0.5, 'y': -0.5},
{'size': 0.5, 'x': 0.5, 'y': -0.5}], max_depth=max_depth, **kwargs)

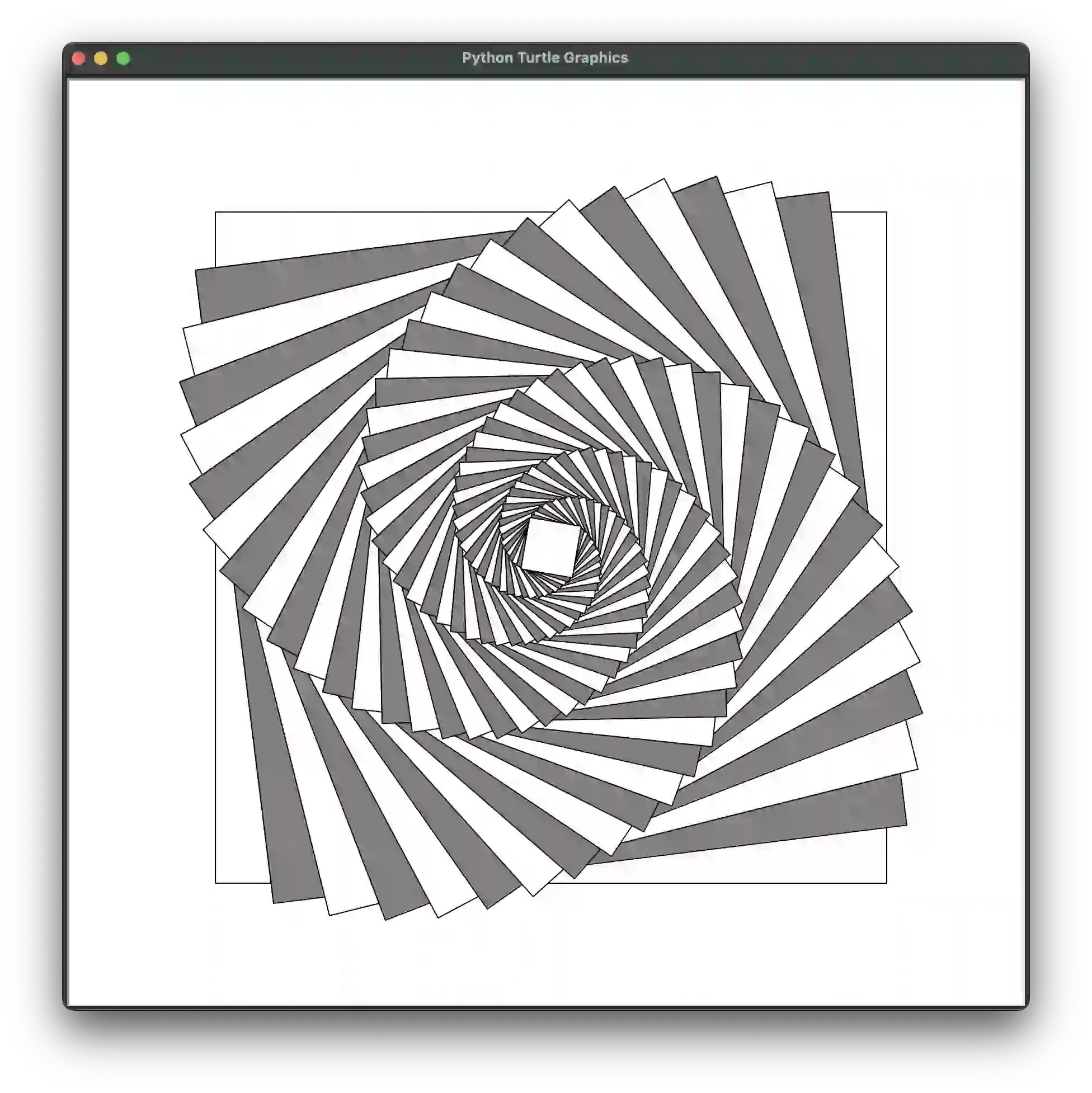
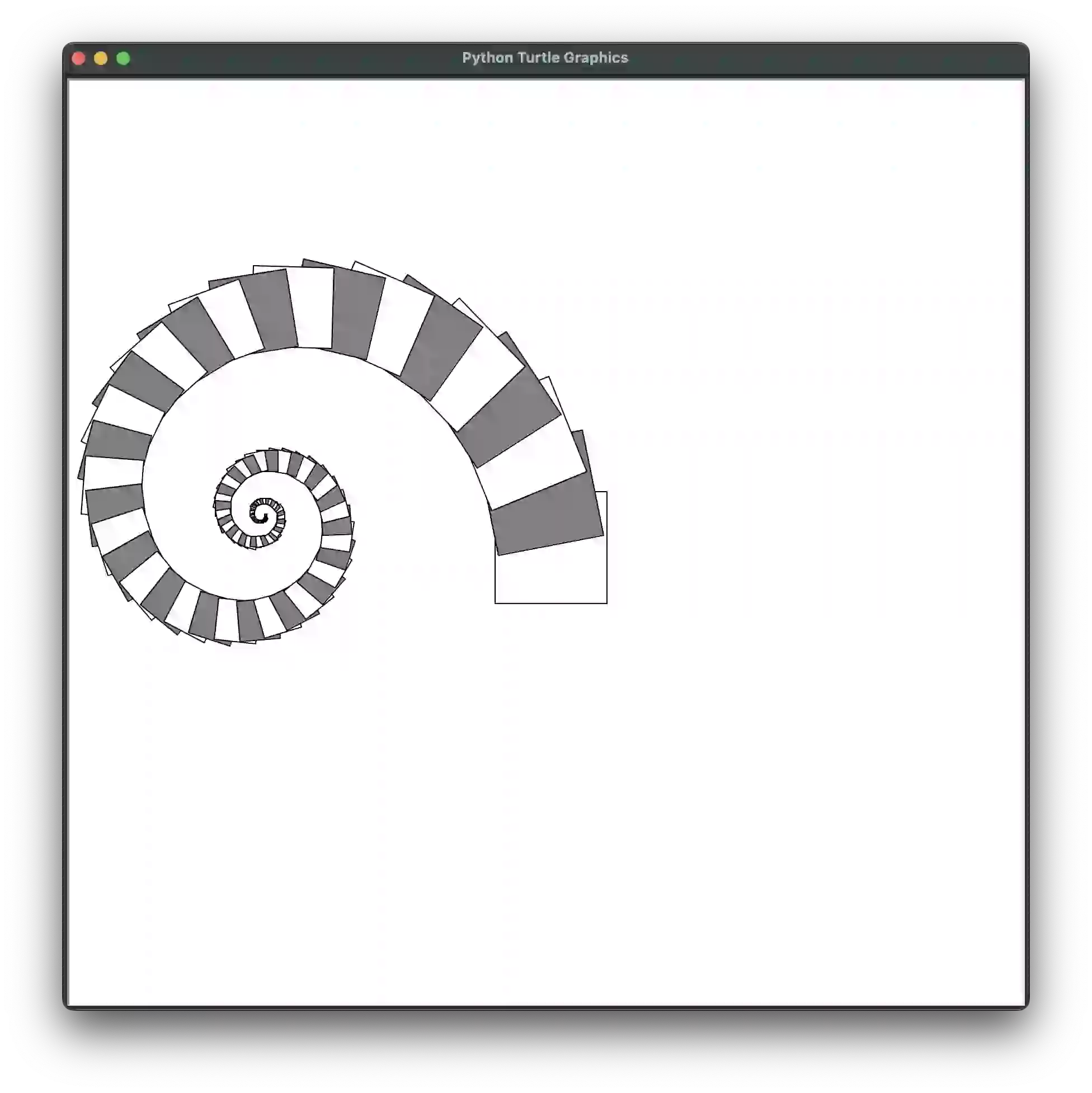
def demo_spiral_squares(size=600, max_depth=50, **kwargs):
# Spiral Squares:
if 'colors' not in kwargs:
kwargs['colors'] = (('black', 'white'), ('black', 'gray'))
draw_fractal(square, size, [{'size': 0.95,
'angle': 7}], max_depth=max_depth, **kwargs)
def demo_double_spiral_squares(size=600, **kwargs):
# Double Spiral Squares:
if 'colors' not in kwargs:
kwargs['colors'] = (('black', 'white'), ('black', 'gray'))
draw_fractal(square, 600,
[{'size': 0.8, 'y': 0.1, 'angle': -10},
{'size': 0.8, 'y': -0.1, 'angle': 10}], **kwargs)
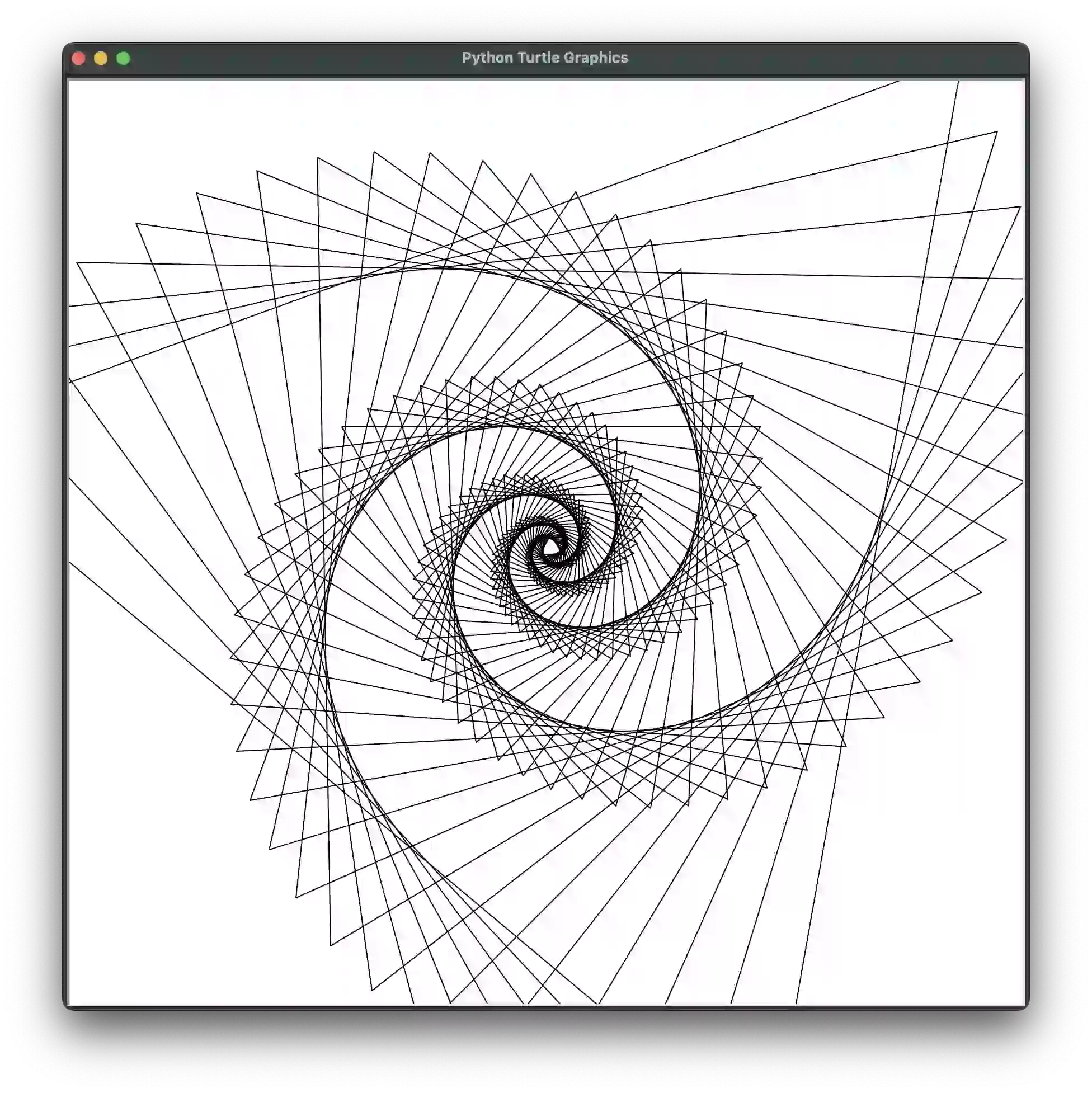
def demo_triangle_spiral(size=20, max_depth=80, **kwargs):
# Triangle Spiral:
draw_fractal(triangle, size,
[{'size': 1.05, 'angle': 7}], max_depth=max_depth, **kwargs)
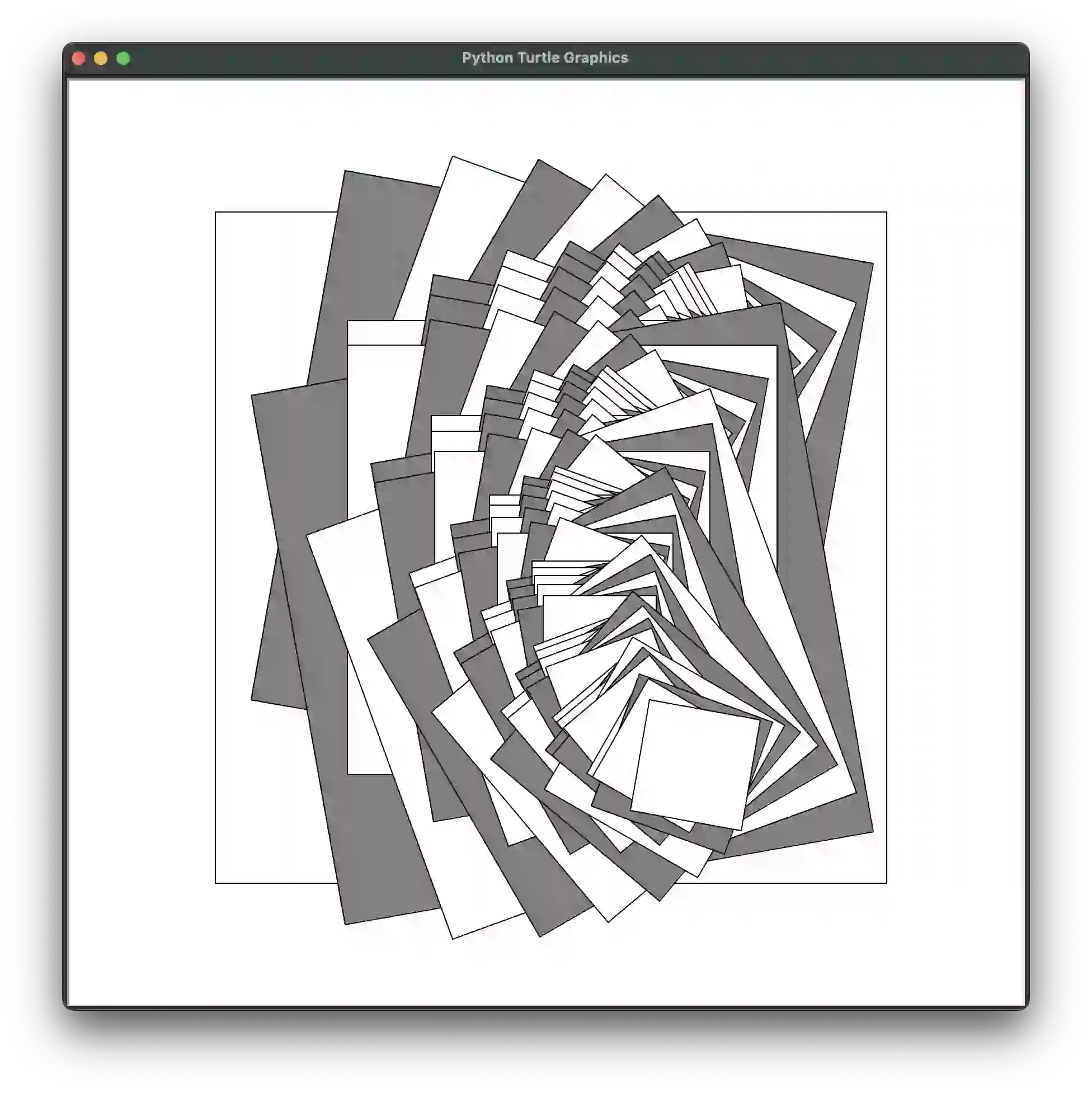
def demo_glider(size=600, **kwargs):
# Conway's Game of Life Glider:
if 'colors' not in kwargs:
kwargs['colors'] = (('black', 'white'), ('black', 'gray'))
third = 1 / 3
draw_fractal(square, 600,
[{'size': third, 'y': third},
{'size': third, 'x': third},
{'size': third, 'x': third, 'y': -third},
{'size': third, 'y': -third},
{'size': third, 'x': -third, 'y': -third}], **kwargs)
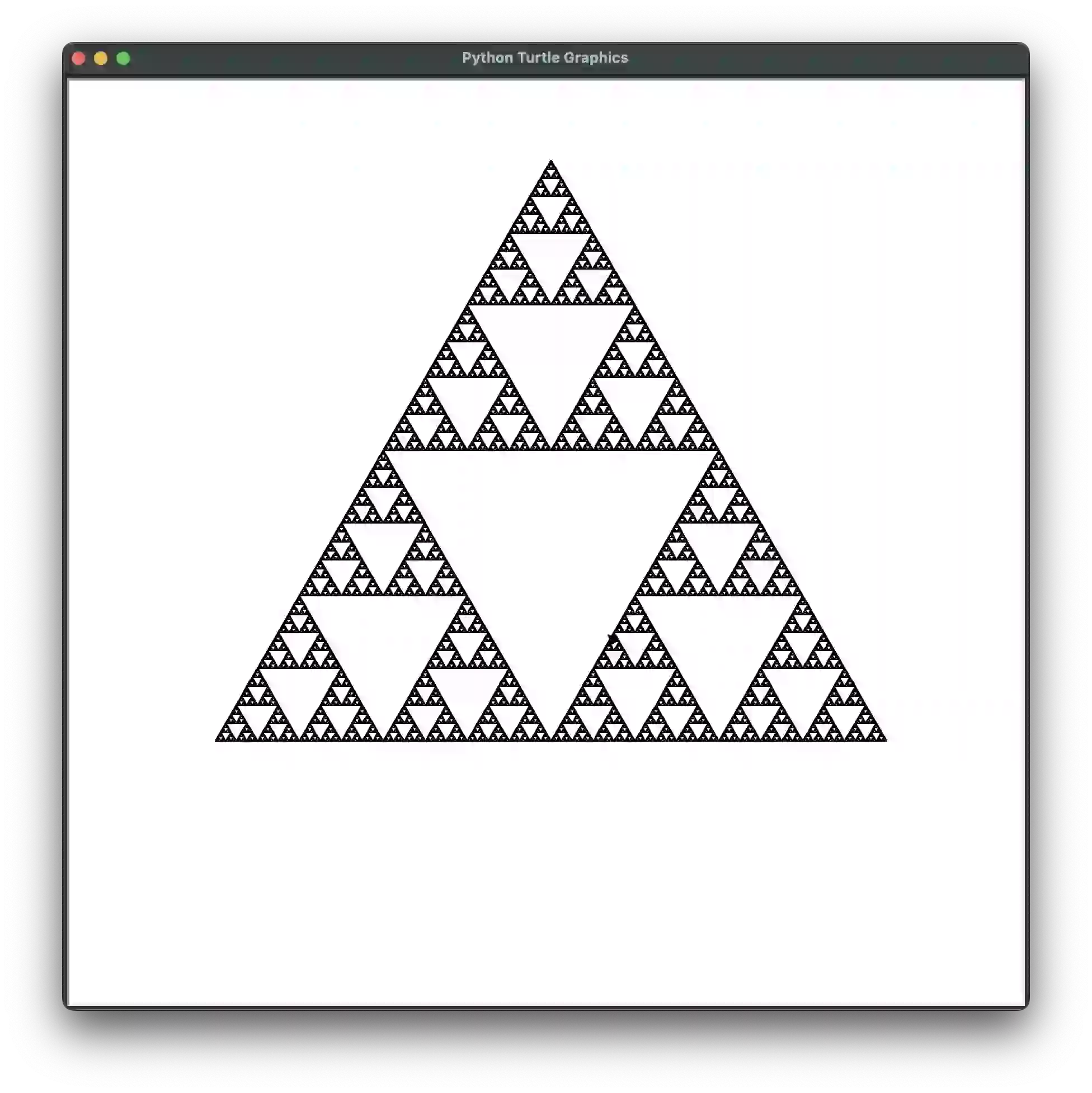
def demo_sierpinski_triangle(size=600, **kwargs):
# Sierpinski Triangle:
toMid = math.sqrt(3) / 6
draw_fractal(triangle, 600,
[{'size': 0.5, 'y': toMid, 'angle': 0},
{'size': 0.5, 'y': toMid, 'angle': 120},
{'size': 0.5, 'y': toMid, 'angle': 240}], **kwargs)
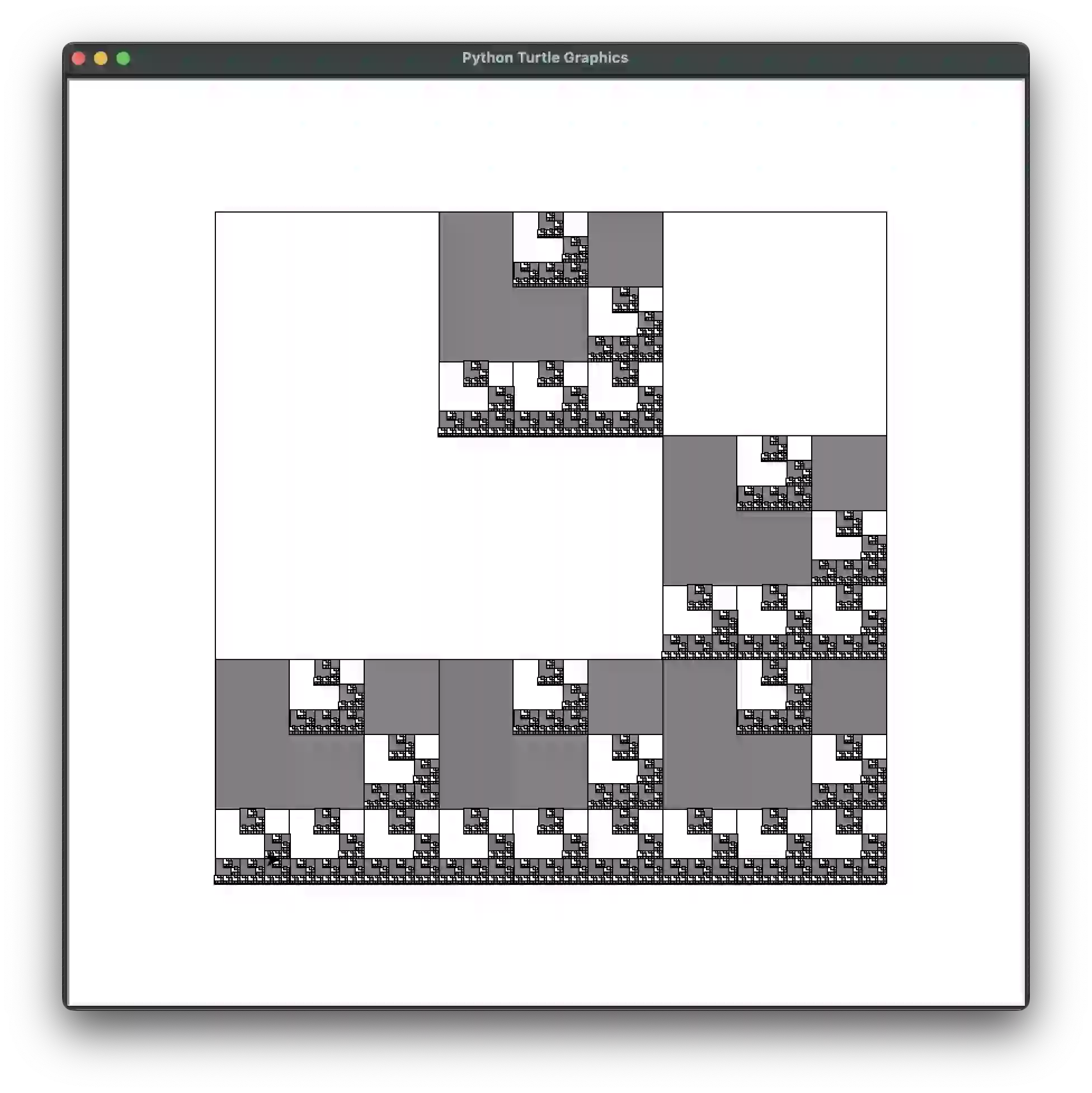
def demo_wave(size=280, **kwargs):
# Wave:
draw_fractal(triangle, size,
[{'size': 0.5, 'x': -0.5, 'y': 0.5},
{'size': 0.3, 'x': 0.5, 'y': 0.5},
{'size': 0.5, 'y': -0.7, 'angle': 15}], **kwargs)
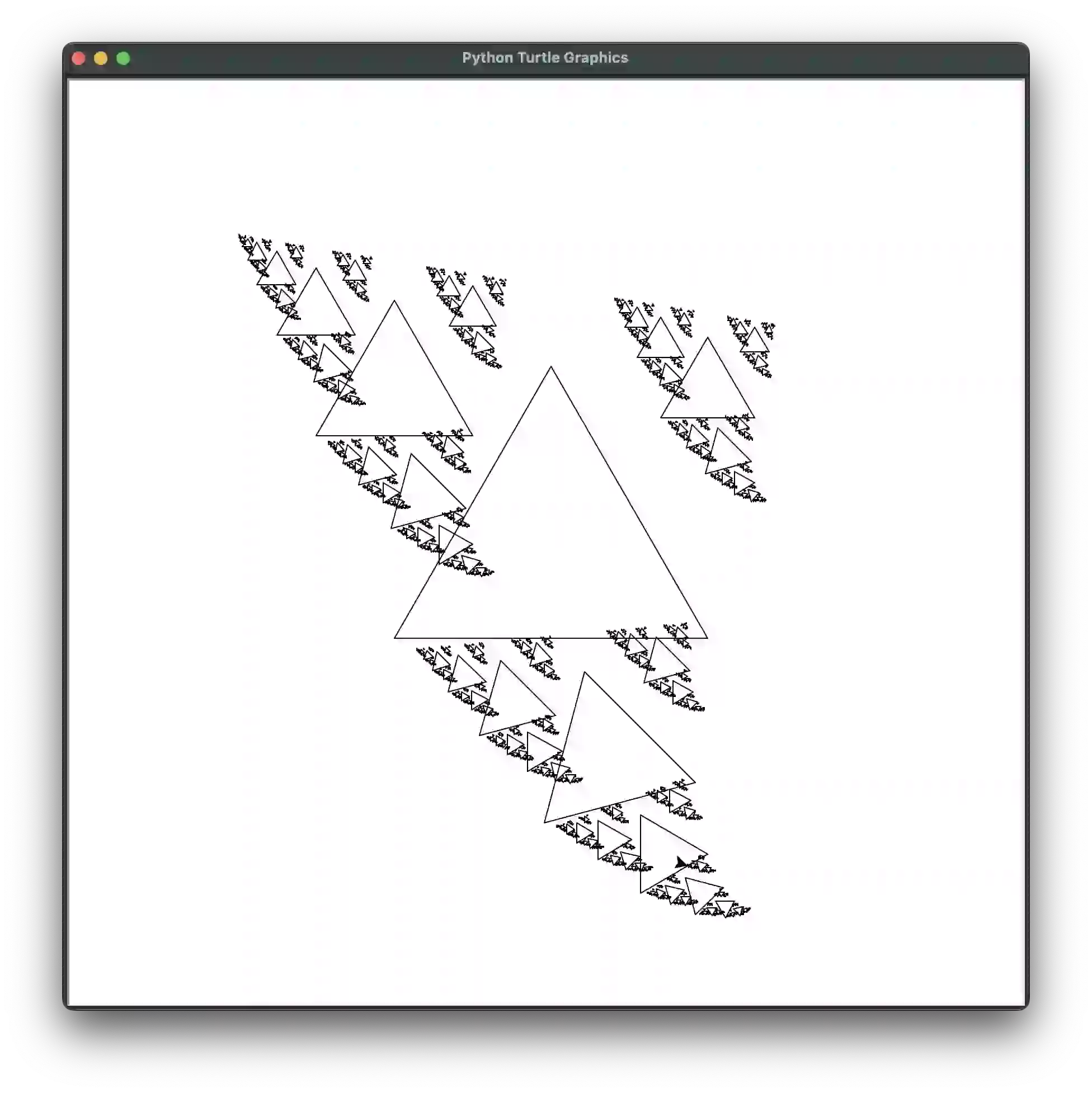
def demo_horn(size=100, max_depth=100, **kwargs):
# Horn:
if 'colors' not in kwargs:
kwargs['colors'] = (('black', 'white'), ('black', 'gray'))
draw_fractal(square, size,
[{'size': 0.96, 'y': 0.5, 'angle': 11}], max_depth=max_depth, **kwargs)
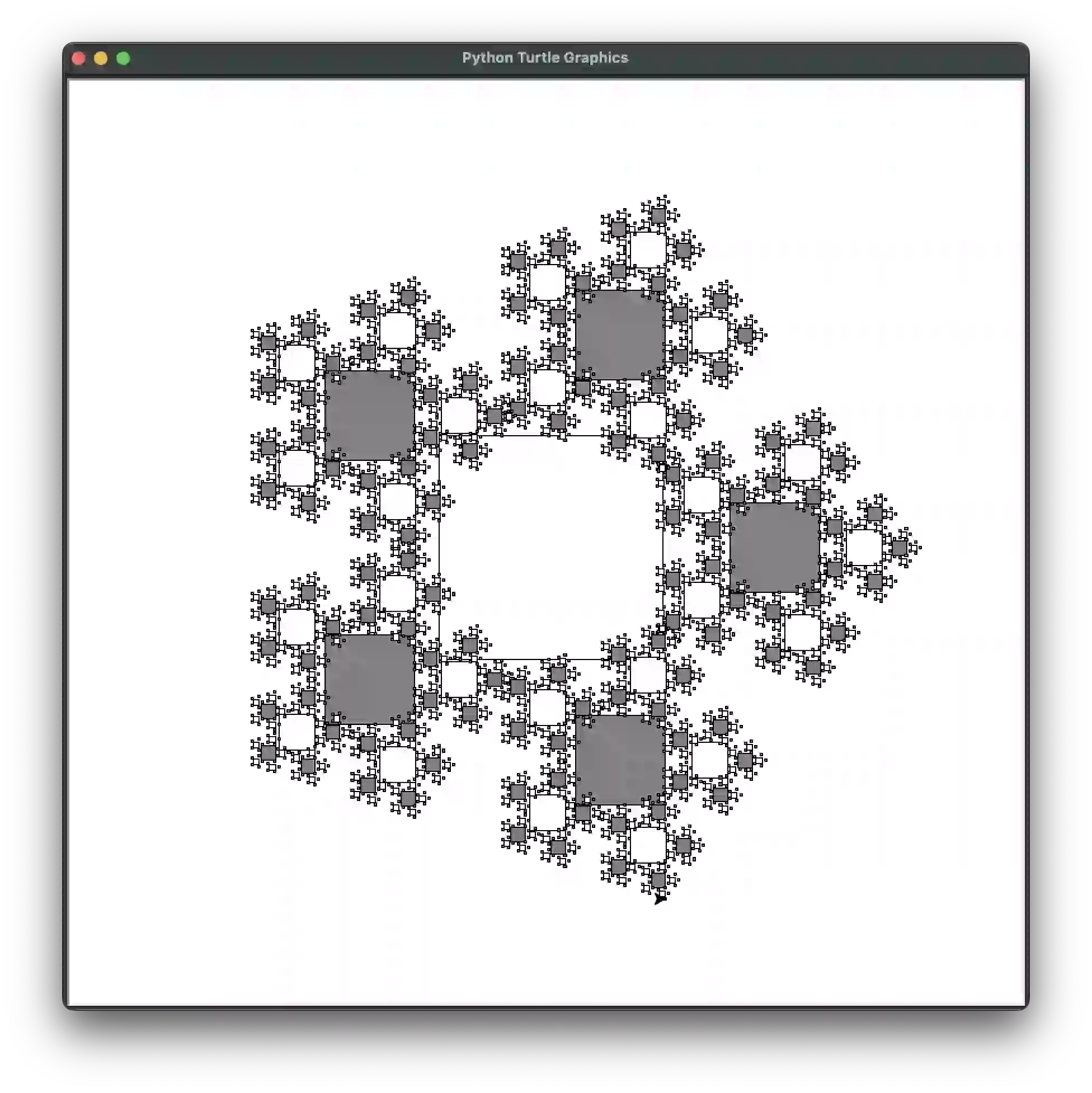
def demo_snowflake(size=200, **kwargs):
# Snowflake:
if 'colors' not in kwargs:
kwargs['colors'] = (('black', 'white'), ('black', 'gray'))
draw_fractal(square, size,
[{'x': math.cos(0 * math.pi / 180),
'y': math.sin(0 * math.pi / 180), 'size': 0.4},
{'x': math.cos(72 * math.pi / 180),
'y': math.sin(72 * math.pi / 180), 'size': 0.4},
{'x': math.cos(144 * math.pi / 180),
'y': math.sin(144 * math.pi / 180), 'size': 0.4},
{'x': math.cos(216 * math.pi / 180),
'y': math.sin(216 * math.pi / 180), 'size': 0.4},
{'x': math.cos(288 * math.pi / 180),
'y': math.sin(288 * math.pi / 180), 'size': 0.4}], **kwargs)
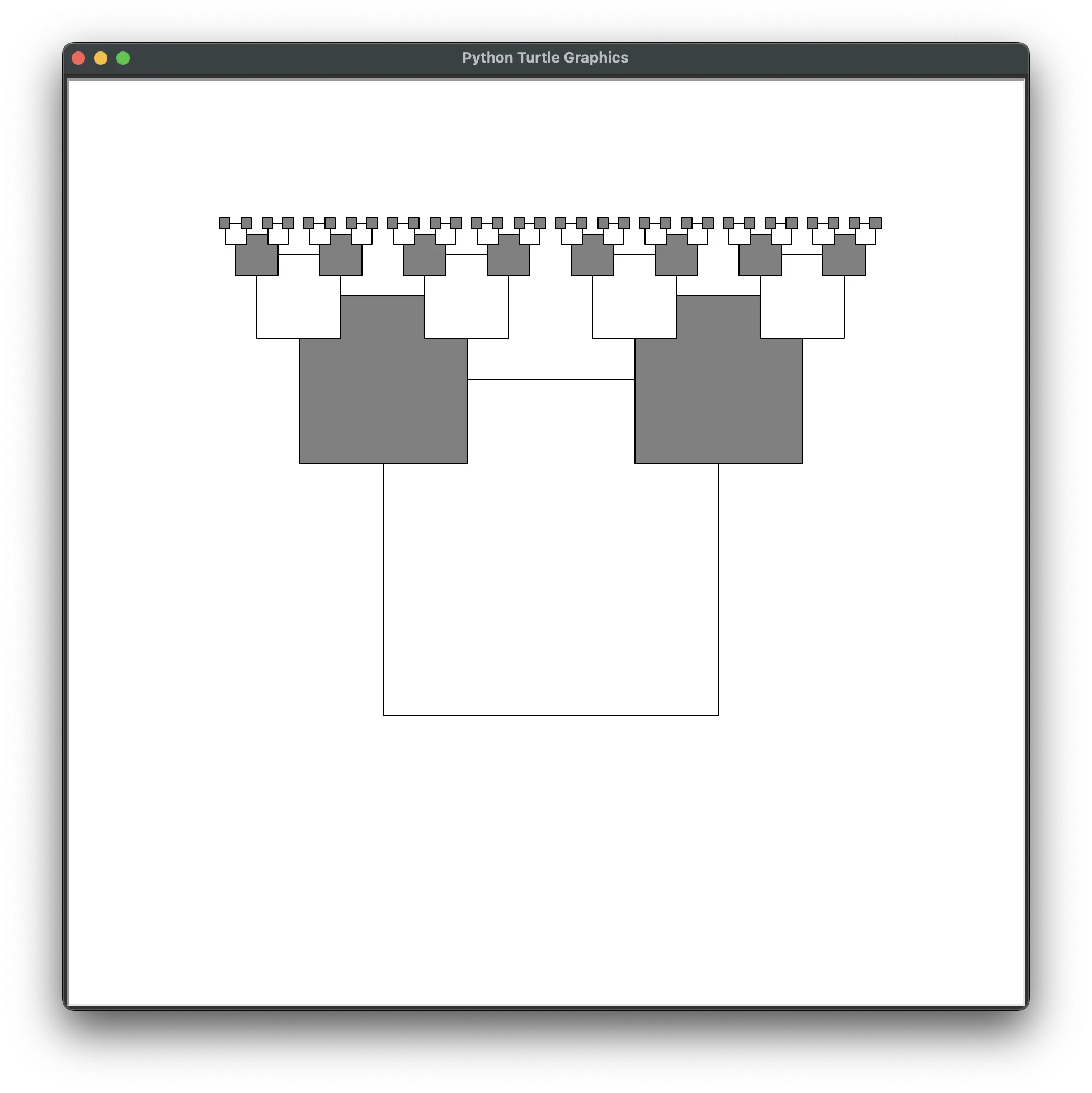
Advanced Features of FAM's Shape-Drawing Functions
All shape-drawing functions are passed a size argument. We can make the white-and-gray alternating colors by adding the optional depth parameter to our drawing function. The draw_fractal() function will pass the recursion depth (1 for the first depth level, 2 for the next, and so on) to the drawing function. In the following square_alternating_white_gray() drawing function, the fill color for the square is set to white or gray depending on the depth argument:
def square_alternating_white_gray(size, depth):
# Move to the top-right corner before drawing:
turtle.penup()
turtle.forward(size // 2)
turtle.left(90)
turtle.forward(size // 2)
turtle.left(180)
turtle.pendown()
# Set fill color based on recursion depth level:
if depth % 2 == 0:
turtle.fillcolor('white')
else:
turtle.fillcolor('gray')
# Draw a square:
turtle.begin_fill()
for i in range(4): # Draw four lines.
turtle.forward(size)
turtle.right(90)
turtle.end_fill()
draw_fractal(square_alternating_white_gray, 300,
[{'size': 0.5, 'x': -0.5, 'y': 0.5},
{'size': 0.5, 'x': 0.5, 'y': 0.5},], max_depth=5)
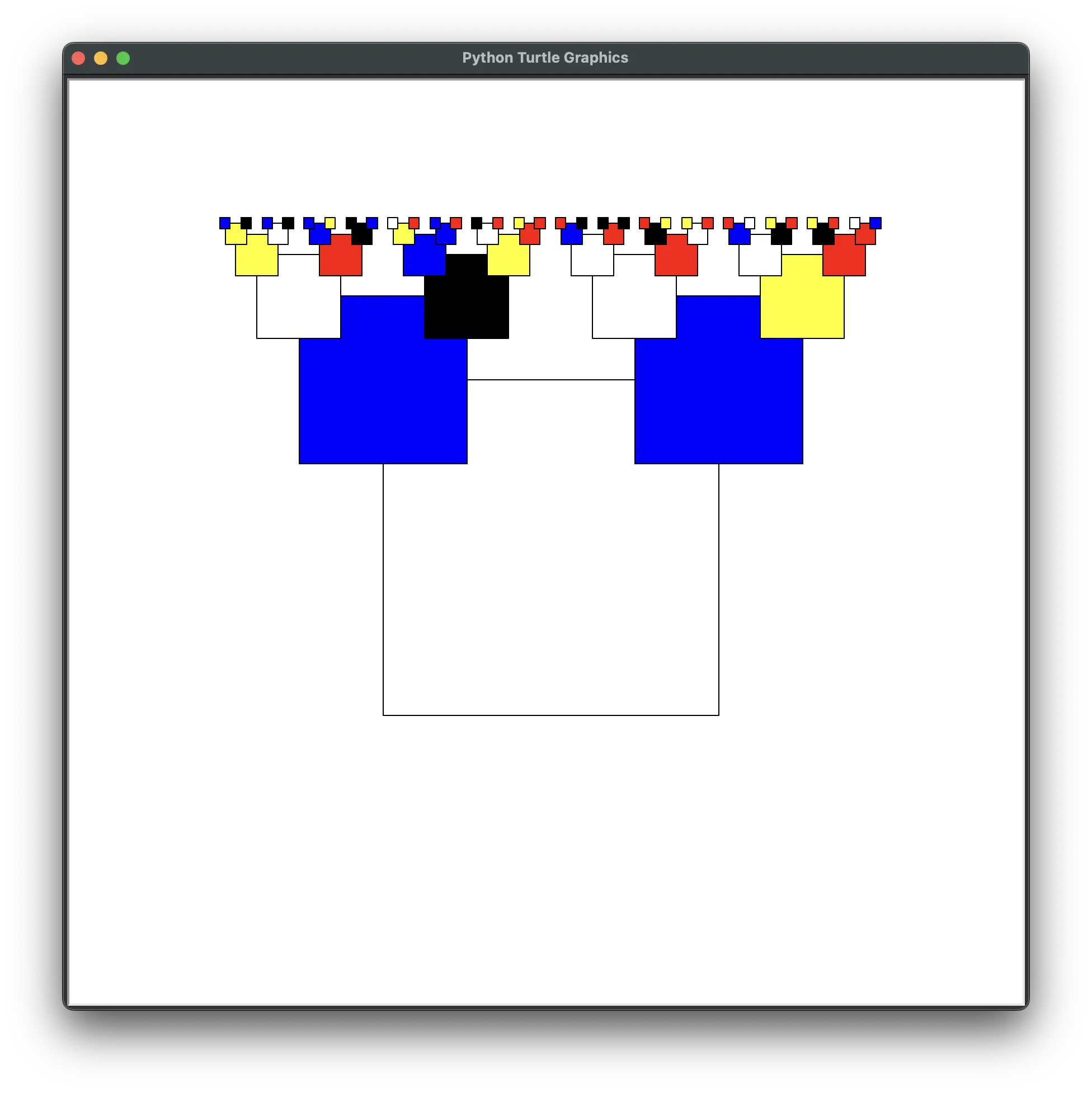
You can also pass any custom keyword argument to draw_fractal(), and it will be forwarded to the drawing function. For example, I set up square_random_fill() draw function with a custom_fill_colors parameter. If you pass custom_fill_colors=['blue', 'red', 'yellow', 'black', 'white'] to draw_fractal(), this list will be forwarded to the draw function. Note that if you pass a custom argument like custom_fill_colors to draw_fractal(), the drawing function must have a parameter named custom_fill_colors.
import random
def square_random_fill(size, custom_fill_colors):
# Move to the top-right corner before drawing:
turtle.penup()
turtle.forward(size // 2)
turtle.left(90)
turtle.forward(size // 2)
turtle.left(180)
turtle.pendown()
# Set fill color randomly:
turtle.fillcolor(random.choice(custom_fill_colors))
# Draw a square:
turtle.begin_fill()
for i in range(4): # Draw four lines.
turtle.forward(size)
turtle.right(90)
turtle.end_fill()
draw_fractal(square_random_fill, 300,
[{'size': 0.5, 'x': -0.5, 'y': 0.5},
{'size': 0.5, 'x': 0.5, 'y': 0.5},], max_depth=5, custom_fill_colors=['blue', 'red', 'yellow', 'black', 'white'])