







Use this link to get 70% off the Automate the Boring Stuff online video course.
Support me on Patreon








“Mathematicians have tried in vain to this day to discover some order in the sequence of prime numbers, and we have reason to believe that it is a mystery into which the human mind will never penetrate.”
—Leonhard Euler, 18th-century mathematician

All the ciphers described in this book so far have been in existence for hundreds of years. These ciphers worked well when hackers had to rely on pencil and paper, but they’re more vulnerable now that computers can manipulate data trillions of times faster than a person can. Another problem with these classical ciphers is that they use the same key for encryption and decryption. Using one key causes problems when you’re trying to send an encrypted message: for example, how can you securely send the key to decrypt it?
In Chapter 23, you’ll learn how the public key cipher improves on the old ciphers by using very large prime numbers to create two keys: a public key for encryption and a private key for decryption. To generate prime numbers for the public key cipher’s keys, you’ll need to learn about some properties of prime numbers (and the difficulty of factoring large numbers) that make the cipher possible. In this chapter, you’ll exploit these features of prime numbers to create the primeNum.py module, which can generate keys by quickly determining whether or not a number is prime.
A prime number is an integer that is greater than 1 and has only two factors: 1 and itself. Recall that the factors of a number are those numbers that can be multiplied to equal the original number. For example, the numbers 3 and 7 are factors of 21. The number 12 has factors 2 and 6 as well as 3 and 4.
Every number has factors of 1 and itself because 1 multiplied by any number will always equal that number. For example, 1 and 21 are factors of 21, and the numbers 1 and 12 are factors of 12. If no other factors exist for a number, the number is prime. For example, 2 is a prime number because it has only 1 and 2 as its factors.
Here is a short list of prime numbers (note that 1 is not considered a prime number): 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, and so on.
There is an infinite number of prime numbers, which means there is no such thing as the largest prime number. They continue to get bigger and bigger, just like regular numbers. The public key cipher uses large prime numbers to make the key too big to brute-force.
Prime numbers can be difficult to find, and large prime numbers, such as those used for public keys, are even harder to find. To generate large prime numbers as public keys, we’ll find a random large number and then check whether the number is prime by using a primality test. If the number is prime according to the primality test, we’ll use it; otherwise, we’ll continue creating and testing large numbers until we find one that is prime.
Let’s look at some very large numbers to illustrate how big the prime numbers used in the public key cipher can be.
A googol is 10 raised to the power of 100 and is written as a 1 followed by 100 zeros:
10,000,000,000,000,000,000,000,000,000,000,000,000,000,000,
000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,
000,000,000,000
A billion billion billion googols have 27 more zeros than a googol:
10,000,000,000,000,000,000,000,000,000,000,000,000,000,000,
000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,
000,000,000,000,000,000,000,000,000,000,000,000,000
But these are tiny numbers compared to the prime numbers the public key cipher uses. For example, a typical prime number used in the public key program has hundreds of digits and might look something like this:
112,829,754,900,439,506,175,719,191,782,841,802,172,556,768,
253,593,054,977,186,2355,84,979,780,304,652,423,405,148,425,
447,063,090,165,759,070,742,102,132,335,103,295,947,000,718,
386,333,756,395,799,633,478,227,612,244,071,875,721,006,813,
307,628,061,280,861,610,153,485,352,017,238,548,269,452,852,
733,818,231,045,171,038,838,387,845,888,589,411,762,622,041,
204,120,706,150,518,465,720,862,068,595,814,264,819
This number is so big that I bet you didn’t even notice the typo in it.
A few other interesting features of prime numbers are also useful to know. Because all even numbers are multiples of two, 2 is the only possible even prime number. Also, multiplying two prime numbers should result in a number whose only factors are 1, itself, and the two prime numbers that were multiplied. (For example, multiplying prime numbers 3 and 7 results in 21, whose only factors are 1, 21, 3, and 7.)
Integers that are not prime are called composite numbers because they’re composed of at least two factors besides 1 and the number. Every composite number has a prime factorization, which is a factorization composed of only prime numbers. For example, the composite number 1386 is composed of the prime numbers 2, 3, 7, and 11, because 2 × 3 × 3 × 7 × 11 = 1386. Each composite number’s prime factorization is unique to that composite number.
We’ll use this information about what makes a number prime to write a module that can determine whether a small number is prime and generate prime numbers. The module, primeNum.py, will define the following functions:
isPrimeTrialDiv() uses the trial division algorithm to return True if the number passed to it is prime or False if the number passed to it is not prime.
primeSieve() uses the sieve of Eratosthenes algorithm to generate prime numbers.
rabinMiller() uses the Rabin-Miller algorithm to check whether the number passed to it is prime. This algorithm, unlike the trial division algorithm, can work quickly on very large numbers. This function is called not directly but rather by isPrime().
isPrime() is called when the user must determine whether a large integer is prime or not.
generateLargePrime() returns a large prime number that is hundreds of digits long. This function will be used in the makePublicPrivateKeys.py program in Chapter 23.
Like cryptomath.py, introduced in Chapter 13, the primeNum.py program is meant to be imported as a module by other programs and doesn’t do anything when run on its own. The primeNum.py module imports Python’s math and random modules to use when generating prime numbers.
Open a new file editor window by selecting File▸New File. Enter the following code into the file editor and then save it as primeNum.py.
primeNum.py
1. # Prime Number Sieve
2. # https://www.nostarch.com/crackingcodes/ (BSD Licensed)
3.
4. import math, random
5.
6.
7. def isPrimeTrialDiv(num):
8. # Returns True if num is a prime number, otherwise False.
9.
10. # Uses the trial division algorithm for testing primality.
11.
12. # All numbers less than 2 are not prime:
13. if num < 2:
14. return False
15.
16. # See if num is divisible by any number up to the square root of num:
17. for i in range(2, int(math.sqrt(num)) + 1):
18. if num % i == 0:
19. return False
20. return True
21.
22.
23. def primeSieve(sieveSize):
24. # Returns a list of prime numbers calculated using
25. # the Sieve of Eratosthenes algorithm.
26.
27. sieve = [True] * sieveSize
28. sieve[0] = False # Zero and one are not prime numbers.
29. sieve[1] = False
30.
31. # Create the sieve:
32. for i in range(2, int(math.sqrt(sieveSize)) + 1):
33. pointer = i * 2
34. while pointer < sieveSize:
35. sieve[pointer] = False
36. pointer += i
37.
38. # Compile the list of primes:
39. primes = []
40. for i in range(sieveSize):
41. if sieve[i] == True:
42. primes.append(i)
43.
44. return primes
45.
46. def rabinMiller(num):
47. # Returns True if num is a prime number.
48. if num % 2 == 0 or num < 2:
49. return False # Rabin-Miller doesn't work on even integers.
50. if num == 3:
51. return True
52. s = num - 1
53. t = 0
54. while s % 2 == 0:
55. # Keep halving s until it is odd (and use t
56. # to count how many times we halve s):
57. s = s // 2
58. t += 1
59. for trials in range(5): # Try to falsify num's primality 5 times.
60. a = random.randrange(2, num - 1)
61. v = pow(a, s, num)
62. if v != 1: # This test does not apply if v is 1.
63. i = 0
64. while v != (num - 1):
65. if i == t - 1:
66. return False
67. else:
68. i = i + 1
69. v = (v ** 2) % num
70. return True
71.
72. # Most of the time we can quickly determine if num is not prime
73. # by dividing by the first few dozen prime numbers. This is quicker
74. # than rabinMiller() but does not detect all composites.
75. LOW_PRIMES = primeSieve(100)
76.
77.
78. def isPrime(num):
79. # Return True if num is a prime number. This function does a quicker
80. # prime number check before calling rabinMiller().
81. if (num < 2):
82. return False # 0, 1, and negative numbers are not prime.
83. # See if any of the low prime numbers can divide num:
84. for prime in LOW_PRIMES:
85. if (num == prime):
86. return True
87. if (num % prime == 0):
88. return False
89. # If all else fails, call rabinMiller() to determine if num is prime:
90. return rabinMiller(num)
91.
92.
93. def generateLargePrime(keysize=1024):
94. # Return a random prime number that is keysize bits in size:
95. while True:
96. num = random.randrange(2**(keysize-1), 2**(keysize))
97. if isPrime(num):
98. return num
To see sample output of the primeNum.py module, enter the following into the interactive shell:
>>> import primeNum
>>> primeNum.generateLargePrime()
122881168342211041030523683515443239007484290600701555369488271748378054744009
463751312511471291011945732413378446666809140502037003673211052153493607681619
990563076859566835016382556518967124921538212397036345815983641146000671635019
637218348455544435908428400192565849620509600312468757953899553441648428119
>>> primeNum.isPrime(45943208739848451)
False
>>> primeNum.isPrime(13)
True
Importing the primeNum.py module lets us generate a very large prime number using the generateLargePrime() function. It also lets us pass any number, large or small, to the isPrime() function to determine whether it’s a prime number.
To find out whether or not a given number is prime, we use the trial division algorithm. The algorithm continues to divide a number by integers (starting with 2, 3, and so on) to see whether any of them evenly divides the number with 0 as the remainder. For example, to test whether 49 is prime, we can try dividing it by integers starting with 2:
49 ÷ 2 = 24 remainder 1
49 ÷ 3 = 16 remainder 1
49 ÷ 4 = 12 remainder 1
49 ÷ 5 = 9 remainder 4
49 ÷ 6 = 8 remainder 1
49 ÷ 7 = 7 remainder 0
Because 7 evenly divides 49 with a remainder of 0, we know that 7 is a factor of 49. This means that 49 can’t be a prime number, because it has at least one factor other than 1 and itself.
We can expedite this process by dividing by prime numbers only, not composite numbers. As mentioned earlier, composite numbers are nothing more than composites of prime numbers. This means that if 2 can’t divide 49 evenly, then a composite number such as 6, whose factors include 2, won’t be able to divide 49 evenly either. In other words, any number that 6 divides evenly can also be divided by 2 evenly, because 2 is a factor of 6. Figure 22-1 illustrates this concept.
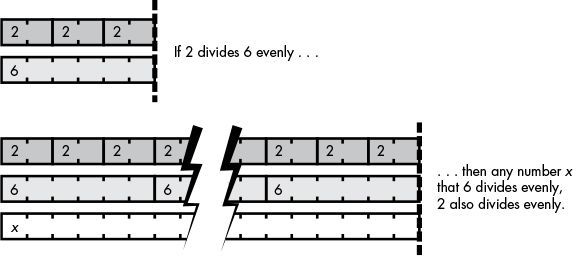
Figure 22-1: Any number that divides evenly by 6 also divides evenly by 2.
As another example, let’s test whether 13 is prime:
13 ÷ 2 = 6 remainder 1
13 ÷ 3 = 4 remainder 1
We only have to test integers up to (and including) the square root of the number we’re testing for primality. The square root of a number refers to the number that when multiplied by itself results in that original number. For example, the square root of 25 is 5 because 5 × 5 = 25. Because a number can’t have two factors greater than its square root, we can limit the trial division algorithm test to integers less than the number’s square root. The square root of 13 is about 3.6, so we only need to divide by 2 and 3 to determine that 13 is prime.
As another example, the number 16 has a square root of 4. Multiplying two numbers greater than 4 will always result in a number greater than 16, and any factors of 16 greater than 4 will always be paired with factors smaller than 4, such as 8 × 2. Therefore, you’ll find all the factors greater than the square root by finding any factors less than the square root.
To find a number’s square root in Python, you can use the math.sqrt() function. Enter the following into the interactive shell to see some examples of how this function works:
>>> import math
>>> 5 * 5
25
>>> math.sqrt(25)
5.0
>>> math.sqrt(10)
3.1622776601683795
Notice that math.sqrt() always returns a floating-point value.
The isPrimeTrialDiv() function on line 7 in primeNum.py takes a number as the parameter num and uses the trial division algorithm test to check whether the number is prime. The function returns False if num is a composite number and True if num is a prime number.
7. def isPrimeTrialDiv(num):
8. # Returns True if num is a prime number, otherwise False.
9.
10. # Uses the trial division algorithm for testing primality.
11.
12. # All numbers less than 2 are not prime:
13. if num < 2:
14. return False
Line 13 checks whether num is less than 2, and if it is, the function returns False, because a number less than 2 cannot be prime.
Line 17 begins the for loop that implements the trial division algorithm. It also takes the square root of num using math.sqrt() and uses the returned floating-point value to set the upper limit of the range of integers we’ll test.
16. # See if num is divisible by any number up to the square root of num:
17. for i in range(2, int(math.sqrt(num)) + 1):
18. if num % i == 0:
19. return False
20. return True
Line 18 checks whether the remainder is 0 using the mod operator (%). If the remainder is 0, num is divisible by i and is therefore not a prime number, and the loop returns False. If the for loop on line 17 never returns False, the function returns True on line 20 to indicate that num is likely a prime number.
The trial division algorithm in the isPrimeTrialDiv() function is useful, but it’s not the only way to test for primality. You can also find prime numbers using the sieve of Eratosthenes.
The sieve of Eratosthenes (pronounced “era-taws-thuh-knees”) is an algorithm that finds all the prime numbers within a range of numbers. To see how this algorithm works, imagine a group of boxes. Each box holds an integer from 1 to 50, all marked as prime, as shown in Figure 22-2.
To implement the sieve of Eratosthenes, we eliminate non-prime numbers from our range until only prime numbers remain. Because 1 is never prime, let’s start by marking number 1 as “not prime.” Then let’s mark all the multiples of two (except for 2) as “not prime.” This means we’ll mark the integers 4 (2 × 2), 6 (2 × 3), 8 (2 × 4), 10, 12, and so on up to 50 as “not prime,” as shown in Figure 22-3.
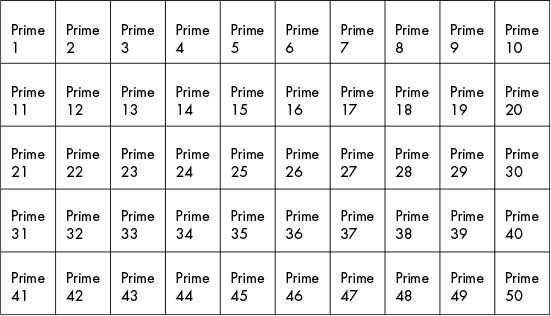
Figure 22-2: Setting up the sieve of Eratosthenes for numbers 1 through 50
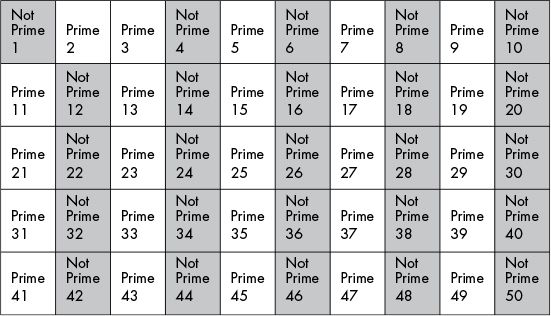
Figure 22-3: Eliminating the number 1 and all even numbers
Then we repeat the process using multiples of three: we exclude 3 and mark 6, 9, 12, 15, 18, 21, and so on as “not prime.” We repeat this process for the multiples of four excluding 4, the multiples of five except for 5, and so on until we get through multiples of eight. We stop at 8 because it is larger than 7.071, which is the square root of 50. All the multiples of 9, 10, 11, and so on will already have been marked, because any number that is a factor larger than the square root will be paired with a factor smaller than the square root, which we’ve already marked.
The completed sieve should look like Figure 22-4, with prime numbers shown in white boxes.
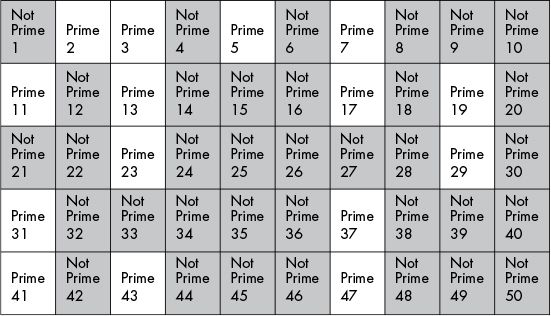
Figure 22-4: Prime numbers found using the sieve of Eratosthenes
Using the sieve of Eratosthenes, we found that the prime numbers less than 50 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, and 47. This sieve algorithm is best used when you want to quickly find all the prime numbers in a certain range of numbers. It’s much faster than using the previous trial division algorithm to check each number individually.
The primeSieve() function on line 23 of the primeNum.py module uses the sieve of Eratosthenes algorithm to return a list of all prime numbers between 1 and sieveSize:
23. def primeSieve(sieveSize):
24. # Returns a list of prime numbers calculated using
25. # the Sieve of Eratosthenes algorithm.
26.
27. sieve = [True] * sieveSize
28. sieve[0] = False # Zero and one are not prime numbers.
29. sieve[1] = False
Line 27 creates a list of Boolean True values that represent the length of sieveSize. The 0 and 1 indexes are marked as False because 0 and 1 are not prime numbers.
The for loop on line 32 goes through each integer from 2 up to the square root of sieveSize:
31. # Create the sieve:
32. for i in range(2, int(math.sqrt(sieveSize)) + 1):
33. pointer = i * 2
34. while pointer < sieveSize:
35. sieve[pointer] = False
36. pointer += i
The variable pointer starts at the first multiple of i after i, which is i * 2 on line 33. Then the while loop sets the pointer index in the sieve list to False, and line 36 changes pointer to point to the next multiple of i.
After the for loop on line 32 finishes, the sieve list should now contain True for each index that is a prime number. We create a new list, which starts as an empty list in primes, loop over the entire sieve list, and append numbers when sieve[i] is True or when i is prime:
38. # Compile the list of primes:
39. primes = []
40. for i in range(sieveSize):
41. if sieve[i] == True:
42. primes.append(i)
Line 44 returns the list of prime numbers:
44. return primes
The primeSieve() function can find all prime numbers within a small range, and the isPrimeTrialDiv() function can quickly determine whether a small number is prime. But what about a large integer that is hundreds of digits long?
If we pass a large integer to isPrimeTrialDiv(), it would take several seconds to determine whether or not it’s prime. And if the number is hundreds of digits long, like the prime numbers we’ll use for the public key cipher program in Chapter 23, it would take more than a trillion years just to figure out whether that number is prime.
In the next section, you’ll learn how to determine whether a very large number is prime using the Rabin-Miller primality test.
The main benefit of the Rabin-Miller algorithm is that it is a relatively simple primality test and takes only a few seconds to run on a normal computer. Even though the algorithm’s Python code is just a few lines long, the explanation of the mathematical proof for why it works would be too long for this book. The Rabin-Miller algorithm is not a surefire test for primality. Instead, it finds numbers that are very likely to be prime but are not guaranteed to be prime. But the chance of a false positive is small enough that this approach is good enough for the purposes of this book. To learn more about how the Rabin-Miller algorithm works, you can read about it at https://en.wikipedia.org/wiki/Miller-Rabin_primality_test.
The rabinMiller() function implements this algorithm to find prime numbers:
46. def rabinMiller(num):
47. # Returns True if num is a prime number.
48. if num % 2 == 0 or num < 2:
49. return False # Rabin-Miller doesn't work on even integers.
50. if num == 3:
51. return True
52. s = num - 1
53. t = 0
54. while s % 2 == 0:
55. # Keep halving s until it is odd (and use t
56. # to count how many times we halve s):
57. s = s // 2
58. t += 1
59. for trials in range(5): # Try to falsify num's primality 5 times.
60. a = random.randrange(2, num - 1)
61. v = pow(a, s, num)
62. if v != 1: # This test does not apply if v is 1.
63. i = 0
64. while v != (num - 1):
65. if i == t - 1:
66. return False
67. else:
68. i = i + 1
69. v = (v ** 2) % num
70. return True
Don’t worry about how this code works. The important concept to keep in mind is that if the rabinMiller() function returns True, the num argument is very likely to be prime. If rabinMiller() returns False, num is definitely composite.
We’ll create another function named isPrime() that will call rabinMiller(). The Rabin-Miller algorithm isn’t always the most efficient way to check whether a number is prime; therefore, at the beginning of the isPrime() function, we’ll do some simple checks as shortcuts to figure out whether the number stored in the parameter num is prime. Let’s store a list of all the primes less than 100 in the constant variable LOW_PRIMES. We can use the primeSieve() function to calculate this list:
72. # Most of the time we can quickly determine if num is not prime
73. # by dividing by the first few dozen prime numbers. This is quicker
74. # than rabinMiller() but does not detect all composites.
75. LOW_PRIMES = primeSieve(100)
We’ll use this list just as we did in isPrimeTrialDiv() and discount any numbers less than 2 (lines 81 and 82):
78. def isPrime(num):
79. # Return True if num is a prime number. This function does a quicker
80. # prime number check before calling rabinMiller().
81. if (num < 2):
82. return False # 0, 1, and negative numbers are not prime.
When num isn’t less than 2, we can use the LOW_PRIMES list as a shortcut to test num, too. Checking whether num is divisible by all the primes less than 100 won’t definitively tell us whether the number is prime, but it might help us find composite numbers. About 90 percent of large integers passed to isPrime() can be detected as composite by dividing by the prime numbers less than 100. The reason is that if the number can be evenly divided by a prime number, such as 3, you don’t have to check whether the number can be evenly divided by composite numbers 6, 9, 12, 15, or any other multiple of 3. Dividing the number by smaller primes is much faster than executing the slower Rabin-Miller algorithm on the number, so this shortcut helps the program execute more quickly about 90 percent of the time isPrime() is called.
Line 85 loops through each of the prime numbers in the LOW_PRIMES list:
83. # See if any of the low prime numbers can divide num:
84. for prime in LOW_PRIMES:
85. if (num == prime):
86. return True
88. return False
If the integer in num is the same as prime, then obviously num must be a prime number and line 86 returns True. The integer in num is modded by each prime number using the mod operator on line 87, and if the result evaluates to 0, we know that prime divides num so num is not prime. In that case, line 88 returns False.
Those are the three quick tests we’ll perform to determine whether a number is prime. If the execution continues past line 87, the rabinMiller() function checks num’s primality.
Line 90 calls the rabinMiller() function to determine whether the number is prime; then the rabinMiller() function takes its return value and returns it from the isPrime() function:
89. # If all else fails, call rabinMiller() to determine if num is prime:
90. return rabinMiller(num)
Now that you know how to determine whether a number is prime, we’ll use these primality tests to generate prime numbers. These will be used by the public key program in Chapter 23.
Using an infinite loop, the generateLargePrime() function on line 93 returns an integer that is prime. It does this by generating a large random number, storing it in num, and then passing num to isPrime(). The isPrime() function then tests whether num is prime.
93. def generateLargePrime(keysize=1024):
94. # Return a random prime number that is keysize bits in size:
95. while True:
96. num = random.randrange(2**(keysize-1), 2**(keysize))
97. if isPrime(num):
98. return num
If num is prime, line 98 returns num. Otherwise, the infinite loop goes back to line 96 to try a new random number. This loop continues until it finds a number that the isPrime() function determines is prime.
The generateLargePrime() function’s keysize parameter has a default value of 1024. The larger the keysize, the more possible keys there are and the harder the cipher is to brute-force. Public key sizes are usually calculated in terms of numbers called bits, which you’ll learn more about in Chapters 23 and 24. For now, just know that a 1024-bit number is very large: it’s about 300 digits!
Prime numbers have fascinating properties in mathematics. As you’ll learn in Chapter 23, they’re also the backbone of ciphers used in professional encryption software. The definition of a prime number is simple enough: it’s a number that has only 1 and itself as factors. But determining which numbers are prime takes some clever code.
In this chapter, we wrote the isPrimeTrialDiv() function to determine whether or not a number is prime by modding a number by all the numbers between 2 and the square root of the number. This is the trial division algorithm. A prime number should never have a remainder of 0 when modded by any number other than its factors, 1 and itself. So we know that a number that has a 0 remainder is not prime.
You learned that the sieve of Eratosthenes can quickly find all prime numbers in a range of numbers, though it uses too much memory for finding large primes.
Because the sieve of Eratosthenes and the trial division algorithm in primeNum.py aren’t fast enough to find large prime numbers, we needed another algorithm for the public key cipher, which uses extremely large prime numbers that are hundreds of digits long. As a workaround, you learned to use the Rabin-Miller algorithm, which uses complex mathematical reasoning to determine whether a very large number is prime.
In Chapter 23, you’ll use the primeNum.py module to write the public key cipher program. At last, you’ll create a cipher that’s easier to use than the one-time pad cipher but cannot be hacked by the simple hacker techniques introduced in this book!