







Use this link to get 70% off the Automate the Boring Stuff online video course.
Support me on Patreon








“Use deliberately compromised cryptography, that has a back door that only the ‘good guys’ are supposed to have the keys to, and you have effectively no security. You might as well skywrite it as encrypt it with pre-broken, sabotaged encryption.”
—Cory Doctorow, science fiction author, 2015

All the ciphers you’ve learned about in this book so far have one feature in common: the encryption key is the same as the decryption key. This leads to a tricky problem: how do you share encrypted messages with someone you’ve never talked to before? Any eavesdroppers would be able to intercept an encryption key you send just as easily as they could intercept the encrypted messages.
In this chapter, you’ll learn about public key cryptography, which allows strangers to share encrypted messages using a public key and a private key. You’ll learn about the public key cipher, which in this book is based on the RSA cipher. Because the RSA cipher is complex and involves multiple steps, you’ll write two programs. In this chapter, you’ll write the public key generation program to generate your public and private keys. Then, in Chapter 24, you’ll write a second program to encrypt and decrypt messages using the public key cipher and applying the keys generated here. Before we dive into the program, let’s explore how public key cryptography works.
Imagine that someone on the other side of the world wants to communicate with you. You both know that spy agencies are monitoring all emails, letters, texts, and phone calls. To send encrypted messages to that person, you both must agree on a secret key to use. But if one of you emails the secret key to the other, the spy agency will intercept this key and then decrypt any future messages encrypted using that key. Secretly meeting in person to exchange the key is impossible. You can try encrypting the key, but this requires sending that secret key for that message to the other person, which will also be intercepted.
Public key cryptography solves this encryption problem by using two keys, one for encryption and one for decryption, and is an example of an asymmetric cipher. Ciphers that use the same key for encryption and decryption, like many of the previous ciphers in this book, are symmetric ciphers.
It’s important to know that a message encrypted using the encryption key (public key) can only be decrypted using the decryption key (private key). So even if someone obtains the encryption key, they won’t be able to read the original message because the encryption key can’t decrypt the message.
The encryption key is called the public key because it can be shared with the entire world. In contrast, the private key, or the decryption key, must be kept secret.
For example, if Alice wants to send Bob a message, Alice finds Bob’s public key or Bob can give it to her. Then Alice encrypts her message to Bob using Bob’s public key. Because the public key cannot decrypt messages, it doesn’t matter that everyone else has access to Bob’s public key.
When Bob receives Alice’s encrypted message, he uses his private key to decrypt it. Only Bob has the private key that can decrypt messages encrypted using his public key. If Bob wants to reply to Alice, he finds her public key and uses it to encrypt his reply. Because only Alice knows her private key, Alice is the only person who can decrypt the encrypted response from Bob. Even if Alice and Bob are on opposite sides of the world, they can exchange messages without fear of interception.
The particular public key cipher we’ll implement in this chapter is based on the RSA cipher, which was invented in 1977 and is named using the initials of the last names of its inventors: Ron Rivest, Adi Shamir, and Leonard Adleman.
The RSA cipher uses large prime numbers hundreds of digits long in its algorithm. It is the reason we discussed the mathematics of prime numbers in Chapter 22. The public key algorithm creates two random prime numbers and then uses complicated math (including finding a modular inverse, which you learned how to do in Chapter 13) to create the public and private keys.
As ingenious as the public key ciphers might sound, there’s a slight problem. For example, imagine you received this email: “Hello. I am Emmanuel Goldstein, leader of the resistance. I would like to communicate secretly with you about important matters. Attached is my public key.”
Using this public key, you can be sure that the messages you send cannot be read by anyone other than the sender of the public key. But how do you know the sender is actually Emmanuel Goldstein? You don’t know whether you’re sending encrypted messages to Emmanuel Goldstein or to a spy agency pretending to be Emmanuel Goldstein to lure you into a trap!
Although public key ciphers and, in fact, all the ciphers in this book can provide confidentiality (keeping the message a secret), they don’t always provide authentication (proof that who you’re communicating with is who they say they are).
Normally, this isn’t a problem with symmetric ciphers, because when you exchange keys with a person, you can see who that person is. However, when you use public key encryption, you don’t need to see a person to get their public key and begin sending them encrypted messages. Authentication is critical to keep in mind when you’re using public key cryptography.
An entire field called public key infrastructure (PKI) manages authentication so you can match public keys to people with some level of security; however, this topic is beyond the scope of this book.
Digital signatures allow you to electronically sign documents using encryption. To understand why digital signatures are necessary, let’s look at the following example email from Alice to Bob:
Dear Bob,
I promise to buy your old broken laptop for one million dollars.
Sincerely,
Alice
This is great news for Bob because he wants to get rid of his worthless laptop for any price. But what if Alice later claims that she didn’t make this promise and that the email Bob received is a fake that she didn’t send. After all, Bob could have easily created this email.
If they met in person, Alice and Bob could simply sign a contract agreeing to the sale. A handwritten signature is not as easy to forge and provides some proof that Alice did make this promise. But even if Alice signed such a contract, took a photo of it with her digital camera, and sent Bob the image file, it’s still conceivable that the image could have been altered.
The RSA cipher (like other public key ciphers) not only encrypts messages but also allows us to digitally sign a file or string. For example, Alice can encrypt a message using her private key, producing ciphertext that only Alice’s public key can decrypt. This ciphertext becomes the digital signature for the file. It isn’t actually a secret because everyone in the world has access to Alice’s public key to decrypt it. But by encrypting a message using her private key, Alice can digitally sign the message in a way that cannot be forged. Because only Alice has access to her private key, only Alice could have produced this ciphertext, and she couldn’t say that Bob forged or altered it!
The guarantee that someone who has authored a message won’t be able to deny authoring that message at a later time is called non-repudiation.
People use digital signatures for many important activities, including cryptocurrency, authentication of public keys, and anonymous web surfing. To find out more, go to https://www.nostarch.com/crackingcodes/. Read on to understand why authentication is as important as a secure cipher.
Even more insidious than someone hacking our encrypted messages is a man-in-the-middle or machine-in-the-middle (MITM) attack. In this type of attack, someone intercepts your message and passes it along without your knowledge. For example, let’s say Emmanuel Goldstein really does want to communicate with you and sends you an unencrypted message with his public key, but the spy agency’s routers intercept it. The agency can replace the public key Emmanuel attached to the email with its own public key, and then send the message on to you. You would have no way of knowing whether the key you received is Emmanuel’s key or the spy agency’s key!
Then when you encrypt a reply to Emmanuel, you’re actually encrypting using the spy agency’s public key, not Emmanuel’s public key. The spy agency would be able to intercept that message, decrypt it and read it, and then reencrypt it using Emmanuel’s actual public key before sending your message to Emmanuel. The agency could do the same with any replies that Emmanuel sends to you. Figure 23-1 shows how the MITM attack works.
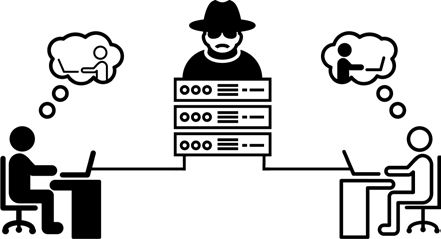
To you and Emmanuel, it looks like you’re communicating with each other in secret. But the spy agency is reading all your messages because you and Emmanuel are encrypting your messages using public keys generated by the spy agency! Again, this problem exists because a public key cipher only provides confidentiality, not authentication. An in-depth discussion of authentication and public key infrastructure is beyond the scope of this book. But now that you know how public key cryptography provides confidentiality, let’s look at how to generate keys for the public key cipher.
Each key in the public key scheme is made of two numbers. The public key will be the two numbers n and e. The private key will be the two numbers n and d.
The three steps to create these numbers are as follows:
Create two random, distinct, very large prime numbers: p and q. Multiply these two numbers to get a number called n.
Create a random number, called e, which is relatively prime to (p – 1) × (q – 1).
Calculate the modular inverse of e, which we’ll call d.
Notice that n is used in both keys. The d number must be kept secret because it can decrypt messages. Now you’re ready to write a program that generates these keys.
Open a new file editor window by selecting File▸New File. Make sure the primeNum.py and cryptomath.py modules are in the same folder as the program file. Enter the following code into the file editor and save it as makePublicPrivateKeys.py.
makePublic
PrivateKeys.py
1. # Public Key Generator
2. # https://www.nostarch.com/crackingcodes/ (BSD Licensed)
3.
4. import random, sys, os, primeNum, cryptomath
5.
6.
7. def main():
8. # Create a public/private keypair with 1024-bit keys:
9. print('Making key files...')
10. makeKeyFiles('al_sweigart', 1024)
11. print('Key files made.')
12.
13. def generateKey(keySize):
14. # Creates public/private keys keySize bits in size.
15. p = 0
16. q = 0
17. # Step 1: Create two prime numbers, p and q. Calculate n = p * q:
18. print('Generating p prime...')
19. while p == q:
20. p = primeNum.generateLargePrime(keySize)
21. q = primeNum.generateLargePrime(keySize)
22. n = p * q
23.
24. # Step 2: Create a number e that is relatively prime to (p-1)*(q-1):
25. print('Generating e that is relatively prime to (p-1)*(q-1)...')
26. while True:
27. # Keep trying random numbers for e until one is valid:
28. e = random.randrange(2 ** (keySize - 1), 2 ** (keySize))
29. if cryptomath.gcd(e, (p - 1) * (q - 1)) == 1:
30. break
31.
32. # Step 3: Calculate d, the mod inverse of e:
33. print('Calculating d that is mod inverse of e...')
34. d = cryptomath.findModInverse(e, (p - 1) * (q - 1))
35.
36. publicKey = (n, e)
37. privateKey = (n, d)
38.
39. print('Public key:', publicKey)
40. print('Private key:', privateKey)
41.
42. return (publicKey, privateKey)
43.
44.
45. def makeKeyFiles(name, keySize):
46. # Creates two files 'x_pubkey.txt' and 'x_privkey.txt' (where x
47. # is the value in name) with the n,e and d,e integers written in
48. # them, delimited by a comma.
49.
50. # Our safety check will prevent us from overwriting our old key files:
51. if os.path.exists('%s_pubkey.txt' % (name)) or
os.path.exists('%s_privkey.txt' % (name)):
52. sys.exit('WARNING: The file %s_pubkey.txt or %s_privkey.txt
already exists! Use a different name or delete these files and
rerun this program.' % (name, name))
53.
54. publicKey, privateKey = generateKey(keySize)
55.
56. print()
57. print('The public key is a %s and a %s digit number.' %
(len(str(publicKey[0])), len(str(publicKey[1]))))
58. print('Writing public key to file %s_pubkey.txt...' % (name))
59. fo = open('%s_pubkey.txt' % (name), 'w')
60. fo.write('%s,%s,%s' % (keySize, publicKey[0], publicKey[1]))
61. fo.close()
62.
63. print()
64. print('The private key is a %s and a %s digit number.' %
(len(str(publicKey[0])), len(str(publicKey[1]))))
65. print('Writing private key to file %s_privkey.txt...' % (name))
66. fo = open('%s_privkey.txt' % (name), 'w')
67. fo.write('%s,%s,%s' % (keySize, privateKey[0], privateKey[1]))
68. fo.close()
69.
70.
71. # If makePublicPrivateKeys.py is run (instead of imported as a module),
72. # call the main() function:
73. if __name__ == '__main__':
74. main()
When we run the makePublicPrivateKeys.py program, the output should look similar to the following (of course, the numbers for your keys will look different because they’re randomly generated):
Making key files...
Generating p prime...
Generating q prime...
Generating e that is relatively prime to (p-1)*(q-1)...
Calculating d that is mod inverse of e...
Public key: (210902406316700502401968491406579417405090396754616926135810621
2161161913380865678407459875355468897928072386270510720443827324671435893274
8583937496850624116776147241821152026946322876869404394483922202407821672864
2424789208131826990008473526711744296548563866768454251404951960805224682425
498975230488955908086491852116348777849536270685085446970952915640050522212
204221803744494065881010331486468305317449607027884787770315729959789994713
265311327663776167710077018340036668306612665759417207845823479903440572724
068125211002329298338718615859542093721097258263595617482450199200740185492
04468791300114315056117093, 17460230769175161021731845459236833553832403910869
129054954200373678580935247606622265764388235752176654737805849023006544732896
308685513669509917451195822611398098951306676600958889189564599581456460070270
393693277683404354811575681605990659145317074127084557233537504102479937142530
0216777273298110097435989)
Private key: (21090240631670050240196849140657941740509039675461692613581062
1216116191338086567840745987535546889792807238627051072044382732467143589327
4858393749685062411677614724182115202694632287686940439448392220240782167286
4242478920813182699000847352671174429654856386676845425140495196080522468242
5498975230488955908086491852116348777849536270685085446970952915640050522212
204221803744494065881010331486468305317449607027884787770315729959789994713
265311327663776167710077018340036668306612665759417207845823479903440572724
068125211002329298338718615859542093721097258263595617482450199200740185492
04468791300114315056117093, 47676735798137710412166884916983765043173120289416
904341295971552286870991874666099933371008075948549008551224760695942666962465
968168995404993934508399014283053710676760835948902312888639938402686187075052
360773062364162664276144965652558545331166681735980981384493349313058750259417
68372702963348445191139635826000818122373486213256488077192893119257248107794
25681884603640028673273135292831170178614206817165802812291528319562200625082
55726168047084560706359601833919317974375031636011432177696164717000025430368
26990539739057474642785416933878499897014777481407371328053001838085314443545
845219087249544663398589)
The public key is a 617 and a 309 digit number.
Writing public key to file al_sweigart_pubkey.txt...
The private key is a 617 and a 309 digit number.
Writing private key to file al_sweigart_privkey.txt...
Because the two keys are very large, they’re each written to their own files, al_sweigart_pubkey.txt and al_sweigart_privkey.txt. We’ll use both files in the public key cipher program in Chapter 24 to encrypt and decrypt messages. These filenames come from the string 'al_sweigart', which is passed to the makeKeyFiles() function on line 10 of the program. You can specify different filenames by passing a different string.
If we run makePublicPrivateKeys.py again and pass the same string to makeKeyFiles(), the output of the program should look like this:
Making key files...
WARNING: The file al_sweigart_pubkey.txt or al_sweigart_privkey.txt already
exists! Use a different name or delete these files and rerun this program.
This warning is provided so we don’t accidentally overwrite our key files, which would make any files encrypted with them impossible to recover. Be sure to keep these key files safe!
When we run makePublicPrivateKeys.py, the main() function is called, which creates the public and private key files using the makeKeyFiles() function that we’ll define shortly.
7. def main():
8. # Create a public/private keypair with 1024-bit keys:
9. print('Making key files...')
10. makeKeyFiles('al_sweigart', 1024)
11. print('Key files made.')
Because the computer might take a while to generate the keys, we print a message on line 9 before the makeKeyFiles() call to let the user know what the program is doing.
The makeKeyFiles() call on line 10 passes the string 'al_sweigart' and the integer 1024, which generates keys that are 1024 bits and stores them in the files al_sweigart_pubkey.txt and al_sweigart_privkey.txt. The larger the key size, the more possible keys there are and the stronger the security of the cipher. However, large key sizes mean that it takes longer to encrypt or decrypt messages. I chose the size of 1024 bits as a balance between speed and security for this book’s examples; but in reality, a key size of 2048 bits or even 3072 bits is necessary for secure public key encryption.
The first step in creating keys is coming up with the two random prime numbers p and q. These numbers must be two large and distinct prime numbers.
13. def generateKey(keySize):
14. # Creates public/private keys keySize bits in size.
15. p = 0
16. q = 0
17. # Step 1: Create two prime numbers, p and q. Calculate n = p * q:
18. print('Generating p prime...')
19. while p == q:
20. p = primeNum.generateLargePrime(keySize)
21. q = primeNum.generateLargePrime(keySize)
22. n = p * q
The generateLargePrime() function you wrote in the primeNum.py program in Chapter 22 returns two prime numbers as integer values on lines 20 and 21, which we store in the variables p and q. This is done inside a while loop that continues to loop as long as p and q are the same. If generateLargePrime() returns the same integer for both p and q, the program will try again to find unique primes for p and q. The value in keySize determines the sizes of p and q. On line 22, we multiply p and q, and store the product in n.
Next, in step 2, we calculate the other piece of the public key: e.
The value for e is calculated by finding a number that is relatively prime to (p – 1) × (q – 1). We won’t go into detail about why e is calculated this way, but we want e to be relatively prime to (p – 1) × (q – 1) because this ensures that e will always result in a unique ciphertext.
Using an infinite while loop, line 26 calculates a number e, which is relatively prime to the product of p – 1 and q – 1.
24. # Step 2: Create a number e that is relatively prime to (p-1)*(q-1):
25. print('Generating e that is relatively prime to (p-1)*(q-1)...')
26. while True:
27. # Keep trying random numbers for e until one is valid:
28. e = random.randrange(2 ** (keySize - 1), 2 ** (keySize))
29. if cryptomath.gcd(e, (p - 1) * (q - 1)) == 1:
30. break
The random.randrange() call on line 28 returns a random integer and stores it in the e variable. Then line 29 tests whether e is relatively prime to (p - 1) * (q - 1) using the cryptomath module’s gcd() function. If e is relatively prime, the break statement on line 30 breaks out of the infinite loop. Otherwise, the program execution jumps back to line 26 and keeps trying different random numbers until it finds one that is relatively prime to (p - 1) * (q - 1).
Next, we calculate the private key.
The third step is to find the other half of the private key used to decrypt, which is d. The d is just the modular inverse of e, and we already have the findModInverse() function in the cryptomath module, which we used in Chapter 13, to calculate that.
Line 34 calls findModInverse() and stores the result in variable d.
32. # Step 3: Calculate d, the mod inverse of e:
33. print('Calculating d that is mod inverse of e...')
34. d = cryptomath.findModInverse(e, (p - 1) * (q - 1))
We’ve now defined all the numbers we need to generate the public and private keys.
Recall that in the public key cipher, the public and private keys consist of two numbers each. The integers stored in n and e represent the public key, and the integers stored in n and d represent the private key. Lines 36 and 37 store these integer pairs as tuple values in publicKey and privateKey.
36. publicKey = (n, e)
37. privateKey = (n, d)
The remaining lines in the generateKey() function print the keys on the screen using print() calls on lines 39 and 40.
39. print('Public key:', publicKey)
40. print('Private key:', privateKey)
41.
42. return (publicKey, privateKey)
Then when generateKey() is called, line 42 returns a tuple containing publicKey and privateKey.
After we’ve generated the public and private keys, we also want to store them in files so our public key cipher program can use them later to encrypt and decrypt. In addition, storing the keys in files is very useful because the two integers that make up each key are hundreds of digits long, making them difficult to memorize or conveniently write down.
The makeKeyFiles() function stores the keys in files by taking a filename and a key size as parameters.
45. def makeKeyFiles(name, keySize):
46. # Creates two files 'x_pubkey.txt' and 'x_privkey.txt' (where x
47. # is the value in name) with the n,e and d,e integers written in
48. # them, delimited by a comma.
The function creates two files in the format <name>_pubkey.txt and <name>_privkey.txt that store the public and private keys, respectively. The name parameter passed to the function determines the <name> part of the files.
To prevent accidentally deleting key files by running the program again, line 51 checks whether the public or private key files with the given name already exist. If they do, the program exits with a warning message.
50. # Our safety check will prevent us from overwriting our old key files:
51. if os.path.exists('%s_pubkey.txt' % (name)) or
os.path.exists('%s_privkey.txt' % (name)):
52. sys.exit('WARNING: The file %s_pubkey.txt or %s_privkey.txt
already exists! Use a different name or delete these files and
rerun this program.' % (name, name))
After this check, line 54 calls generateKey() and passes keySize to create the public and private keys of the size specified.
54. publicKey, privateKey = generateKey(keySize)
The generateKey() function returns a tuple of two tuples that it assigns to the publicKey and privateKey variables using multiple assignment. The first tuple has two integers for the public key, and the second tuple has two integers for the private key.
Now that we’ve finished the setup for creating the key files, we can make the actual key files. We’ll store the two numbers that make up each key in text files.
Line 56 prints an empty line, and then line 57 prints information about the public key for the user.
56. print()
57. print('The public key is a %s and a %s digit number.' %
(len(str(publicKey[0])), len(str(publicKey[1]))))
58. print('Writing public key to file %s_pubkey.txt...' % (name))
Line 57 indicates how many digits are in the integer at publicKey[0] and publicKey[1] by converting those values to strings using the str() function and then finding the length of the string using the len() function. Then, line 58 reports that the public key is being written to the file.
The key file’s contents include the key size, a comma, the n integer, another comma, and the e (or d) integer. For example, the file’s contents should look like this: key size integer, n integer, e or d integer, as in the following al_sweigart_pubkey.txt file:

Lines 59 to 61 open the <name>_pubkey.txt file in write mode, write the keys to the file, and close it.
59. fo = open('%s_pubkey.txt' % (name), 'w')
60. fo.write('%s,%s,%s' % (keySize, publicKey[0], publicKey[1]))
61. fo.close()
Lines 63 to 68 do the same thing as lines 56 to 61 except they write the private key to the <name>_privkey.txt file.
63. print()
64. print('The private key is a %s and a %s digit number.' %
(len(str(publicKey[0])), len(str(publicKey[1]))))
65. print('Writing private key to file %s_privkey.txt...' % (name))
66. fo = open('%s_privkey.txt' % (name), 'w')
67. fo.write('%s,%s,%s' % (keySize, privateKey[0], privateKey[1]))
68. fo.close()
Be sure that nobody hacks your computer and copies these key files. If they obtain your private key file, they’ll be able to decrypt all your messages!
At the end of the program, lines 73 and 74 call the main() function if makePublicPrivateKeys.py is being run as a program instead of being imported as a module by another program.
71. # If makePublicPrivateKeys.py is run (instead of imported as a module),
72. # call the main() function:
73. if __name__ == '__main__':
74. main()
Now you have a program that can generate public and private keys. Although the public key cipher is useful for starting communications between two people who don’t have a way to securely exchange keys, it’s usually not used for all encrypted communication because of the drawbacks of public key cryptography. Often, public key ciphers are instead used in hybrid cryptosystems.
RSA and public key encryption take lots of time to compute. This is especially true for servers that need to make thousands of encrypted connections with other computers per second. As a workaround, people can use public key encryption to encrypt and distribute the key for a much faster symmetric key cipher, which is any type of cipher where the decryption and encryption keys are the same. After securely sending the symmetric cipher’s key to the receiver using a public key–encrypted message, the sender can use the symmetric cipher for future messages. Using both a symmetric key cipher and an asymmetric key cipher to communicate is called a hybrid cryptosystem. You can read more about hybrid cryptosystems at https://en.wikipedia.org/wiki/Hybrid_cryptosystem.
In this chapter, you learned how public key cryptography works and how to write a program that generates the public and private keys. In Chapter 24, you’ll use these keys to perform encryption and decryption using the public key cipher.