Check out other books by Al Sweigart, free online or available for purchase:




...and other books as well! Or register for the online video course. You can also donate to support the author directly.





Recursion has an intimidating reputation. It’s considered hard to understand, but at its core, it depends on only two things: function calls and stack data structures.
Most new programmers trace through what a program does by following the execution. It’s an easy way to read code: you just put your finger on the line of code at the top of the program and move down. Sometimes your finger will loop back; other times, it will jump into a function and later return. This makes it easy to visualize what a program does and in what order.
But to understand recursion, you need to become familiar with a less obvious data structure, called the call stack, that controls the program’s flow of execution. Most programming beginners don’t know about stacks, because programming tutorials often don’t even mention them when discussing function calls. Furthermore, the call stack that automatically manages function calls doesn’t appear anywhere in the source code.
It’s hard to understand something when you can’t see it and don’t know it exists! In this chapter, we’ll pull back the curtain to dispel the overblown notion that recursion is hard, and you’ll be able to appreciate the elegance underneath.
Before we begin, let’s get the clichéd recursion jokes out of the way, starting with this: “To understand recursion, you must first understand recursion.”
During the months I’ve spent writing this book, I can assure you that this joke gets funnier the more you hear it.
Another joke is that if you search Google for recursion, the results page asks if you mean recursion. Following the link, as shown in Figure 1-1, takes you to . . . the search results for recursion.
Figure 1-1: The Google search results for recursion link to the Google search results for recursion.
Figure 1-2 shows a recursion joke from the webcomic xkcd.

Figure 1-2: I’m So Meta, Even This Acronym (I.S. M.E.T.A.) (xkcd.com/917 by Randall Munroe)
Most jokes about the 2010 science fiction action movie Inception are recursion jokes. The film features characters having dreams within dreams within dreams.
And finally, what computer scientist could forget that monster from Greek mythology, the recursive centaur? As you can see in Figure 1-3, it is half horse, half recursive centaur.

Figure 1-3: The recursive centaur. Image by Joseph Parker.
Based on these jokes, you might conclude that recursion is a sort of meta, self-referencing, dream-within-a-dream, infinite mirror-into-mirror sort of thing. Let’s establish a concrete definition: a recursive thing is something whose definition includes itself. That is, it has a self-referential definition.
The Sierpiński triangle in Figure 1-4 is defined as an equilateral triangle with an upside-down triangle in the middle that forms three new equilateral triangles, each of which contains a Sierpiński triangle. The definition of Sierpiński triangles includes Sierpiński triangles.
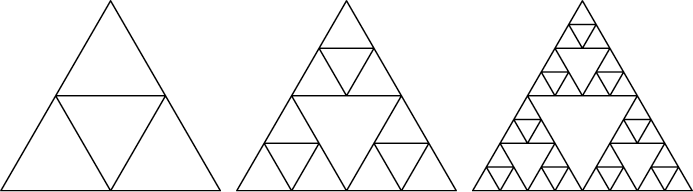
Figure 1-4: Sierpiński triangles are fractals (recursive shapes) that include Sierpiński triangles.
In a programming context, a recursive function is a function that calls itself. Before we explore recursive functions, let’s take a step back and understand how regular functions work. Programmers tend to take function calls for granted, but even experienced programmers will find it worthwhile to review functions in the next section.
Functions can be described as mini-programs inside your program. They’re a feature of nearly every programming language. If you need to run identical instructions at three different places in a program, instead of copying and pasting the source code three times you can write the code in a function once and call the function three times. The beneficial result is a shorter and more readable program. The program is also easier to change: if you need to fix a bug or add features, you need to change your program in only one place instead of three.
All programming languages implement four features in their functions:
undefined or None.Different programming languages might have additional features, or different options for how to call functions, but they all have these four general elements. You can visually see the first three of these elements because you write them in the source code, but how does a program keep track of where the execution should return to when the function returns?
To get a better sense of the problem, create a functionCalls.py program that has three functions: a(), which calls b(), which calls c():
Python
def a():
print('a() was called.')
b()
print('a() is returning.')
def b():
print('b() was called.')
c()
print('b() is returning.')
def c():
print('c() was called.')
print('c() is returning.')
a()This code is equivalent to the following functionCalls.html program:
JavaScript
<script type="text/javascript">
function a() {
document.write("a() was called.<br />");
b();
document.write("a() is returning.<br />");
}
function b() {
document.write("b() was called.<br />");
c();
document.write("b() is returning.<br />");
}
function c() {
document.write("c() was called.<br />");
document.write("c() is returning.<br />");
}
a();
</script>When you run this code, the output looks like this:
a() was called.
b() was called.
c() was called.
c() is returning.
b() is returning.
a() is returning.The output shows the start of functions a(), b(), and c(). Then, when the functions return, the output appears in reverse order: c(), b(), and then a(). Notice the pattern to the text output: each time a function returns, it remembers which line of code originally called it. When the c() function call ends, the program returns to the b() function and displays b() is returning. Then the b() function call ends, and the program returns to the a() function and displays a() is returning. Finally, the program returns to the original a() function call at the end of the program. In other words, function calls don’t send the execution of the program on a one-way trip.
But how does the program remember if it was a() or b() that called c()? This detail is handled by the program implicitly with a call stack. To understand how call stacks remember where the execution returns at the end of a function call, we need to first understand what a stack is.
Earlier I mentioned the clichéd wisecrack, “To understand recursion, you must first understand recursion.” But this is actually wrong: to really understand recursion, you must first understand stacks.
A stack is one of the simplest data structures in computer science. It stores multiple values like a list does—but unlike lists, it limits you to adding to or removing values from the “top” of the stack only. For stacks implemented with lists or arrays, the “top” is the last item, at the right end of the list or array. Adding values is called pushing values onto the stack, while removing values is called popping values off the stack.
Imagine that you’re engaged in a meandering conversation with someone. You’re talking about your friend Alice, which then reminds you of a story about your co-worker Bob, but for that story to make sense, you first have to explain something about your cousin Carol. You finish your story about Carol and go back to talking about Bob, and when you finish your story about Bob, you go back to talking about Alice. Then you are reminded about your brother David, so you tell a story about him. Eventually, you get around to finishing your original story about Alice.
Your conversation follows a stack-like structure, as in Figure 1-5. The conversation is stack-like because the current topic is always at the top of the stack.

Figure 1-5: Your meandering conversation stack
In our conversation stack, the new topics are added to the top of the stack and taken off as they are completed. The previous topics are “remembered” underneath the current topic in the stack.
We can use Python lists as stacks if, to amend the list’s contents, we limit ourselves to the append() and pop() methods to perform pushing and popping. JavaScript arrays can also be used as stacks through their push() and pop() methods.
For example, consider this cardStack.py program, which pushes and pops string values of playing cards to the end of a list named cardStack:
Python
cardStack = ❶ []
❷ cardStack.append('5 of diamonds')
print(','.join(cardStack))
cardStack.append('3 of clubs')
print(','.join(cardStack))
cardStack.append('ace of hearts')
print(','.join(cardStack))
❸ cardStack.pop()
print(','.join(cardStack))The following cardStack.html program contains the equivalent code in JavaScript:
JavaScript
<script type="text/javascript">
let cardStack = ❶ [];
❷ cardStack.push("5 of diamonds");
document.write(cardStack + "<br />");
cardStack.push("3 of clubs");
document.write(cardStack + "<br />");
cardStack.push("ace of hearts");
document.write(cardStack + "<br />");
❸ cardStack.pop()
document.write(cardStack + "<br />");
</script>When you run this code, the output looks like this:
5 of diamonds
5 of diamonds,3 of clubs
5 of diamonds,3 of clubs,ace of hearts
5 of diamonds,3 of clubsThe stack starts off as empty ❶. Three strings representing cards are pushed onto the stack ❷. Then the stack is popped ❸, which removes the ace of hearts and leaves the three of clubs at the top of the stack again. The state of the cardStack stack is tracked in Figure 1-6, going from left to right.
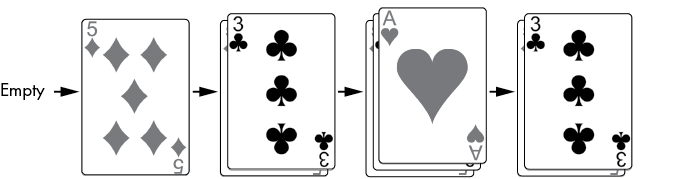
Figure 1-6: The stack starts empty. Cards are then pushed onto and popped off the stack.
You can see only the topmost card in the card stack, or, in our program’s stacks, the topmost value. In the simplest stack implementations, you can’t see how many cards (or values) are in the stack. You can see only whether the stack is empty or not.
Stacks are a LIFO data structure, which stands for last in, first out, since the last value pushed onto the stack is the first value popped out of it. This behavior is similar to your web browser’s Back button. Your browser tab’s history functions like a stack that contains all the pages you’ve visited in the order that you visited them. The browser is always displaying the web page at the “top” of the history’s “stack.” Clicking a link pushes a new web page onto the history stack, while clicking the Back button pops the top web page off and reveals the one “underneath.”
Programs use stacks too. The program’s call stack, also simply called the stack, is a stack of frame objects. Frame objects, also simply called frames, contain information about a single function call, including which line of code called the function, so the execution can move back there when the function returns.
Frame objects are created and pushed onto the stack when a function is called. When the function returns, that frame object is popped off the stack. If we call a function that calls a function that calls a function, the call stack will have three frame objects on the stack. When all these functions return, the call stack will have zero frame objects on the stack.
Programmers don’t have to write code dealing with frame objects, since the programming language handles them automatically. Different programming languages have different ways of implementing frame objects, but in general they contain the following:
For example, take a look at the following localVariables.py program, which has three functions, just as our previous functionCalls.py and functionCalls.html programs did:
Python
def a():
❶ spam = 'Ant'
❷ print('spam is ' + spam)
❸ b()
print('spam is ' + spam)
def b():
❹ spam = 'Bobcat'
print('spam is ' + spam)
❺ c()
print('spam is ' + spam)
def c():
❻ spam = 'Coyote'
print('spam is ' + spam)
❼ a()This localVariables.html is the equivalent JavaScript program:
JavaScript
<script type="text/javascript">
function a() {
❶ let spam = "Ant";
❷ document.write("spam is " + spam + "<br />");
❸ b();
document.write("spam is " + spam + "<br />");
}
function b() {
❹ let spam = "Bobcat";
document.write("spam is " + spam + "<br />");
❺ c();
document.write("spam is " + spam + "<br />");
}
function c() {
❻ let spam = "Coyote";
document.write("spam is " + spam + "<br />");
}
❼ a();
</script>When you run this code, the output looks like this:
spam is Ant
spam is Bobcat
spam is Coyote
spam is Bobcat
spam is AntWhen the program calls function a() ❼, a frame object is created and placed on the top of the call stack. This frame stores any arguments passed to a() (in this case, there are none), along with the local variable spam ❶ and the place where the execution should go when the a() function returns.
When a() is called, it displays the contents of its local spam variable, which is Ant ❷. When the code in a() calls function b() ❸, a new frame object is created and placed on the call stack above the frame object for a(). The b() function has its own local spam variable ❹, and calls c() ❺. A new frame object for the c() call is created and placed on the call stack, and it contains c()’s local spam variable ❻. As these functions return, the frame objects pop off the call stack. The program execution knows where to return to, because that return information is stored in the frame object. When the execution has returned from all function calls, the call stack is empty.
Figure 1-7 shows the state of the call stack as each function is called and returns. Notice that all the local variables have the same name: spam. I did this to highlight the fact that local variables are always separate variables with distinct values, even if they have the same name as local variables in other functions.
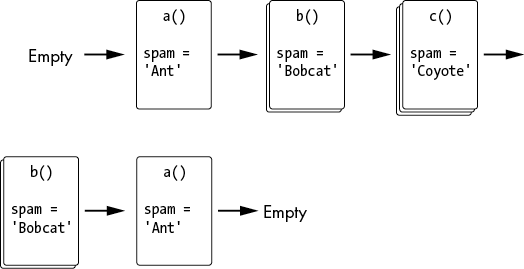
Figure 1-7: The state of the call stack as the localVariables program runs
As you can see, programming languages can have separate local variables with the same name (spam) because they are kept in separate frame objects. When a local variable is used in the source code, the variable with that name in the topmost frame object is used.
Every running program has a call stack, and multithreaded programs have one call stack for each thread. But when you look at the source code for a program, you can’t see the call stack in the code. The call stack isn’t stored in a variable as other data structures are; it’s automatically handled in the background.
The fact that the call stack doesn’t exist in source code is the main reason recursion is so confusing to beginners: recursion relies on something the programmer can’t even see! Revealing how stack data structures and the call stack work removes much of the mystery behind recursion. Functions and stacks are both simple concepts, and we can use them together to understand how recursion works.
A recursive function is a function that calls itself. This shortest.py program is the shortest possible example of a recursive function:
Python
def shortest():
shortest()
shortest()The preceding program is equivalent to this shortest.html program:
JavaScript
<script type="text/javascript">
function shortest() {
shortest();
}
shortest();
</script>The shortest() function does nothing but call the shortest() function. When this happens, it calls the shortest() function again, and that will call shortest(), and so on, seemingly forever. It is similar to the mythological idea that the crust of the Earth rests on the back of a giant space turtle, which rests on the back of another turtle. Beneath that turtle: another turtle. And so on, forever.
But this “turtles all the way down” theory doesn’t do a good job of explaining cosmology, nor recursive functions. Since the call stack uses the computer’s finite memory, this program cannot continue forever, the way an infinite loop does. The only thing this program does is crash and display an error message.
The Python output of shortest.py looks like this:
Traceback (most recent call last):
File "shortest.py", line 4, in <module>
shortest()
File "shortest.py", line 2, in shortest
shortest()
File "shortest.py", line 2, in shortest
shortest()
File "shortest.py", line 2, in shortest
shortest()
[Previous line repeated 996 more times]
RecursionError: maximum recursion depth exceededThe JavaScript output of shortest.html looks like this in the Google Chrome web browser (other browsers will have similar error messages):
Uncaught RangeError: Maximum call stack size exceeded
at shortest (shortest.html:2)
at shortest (shortest.html:3)
at shortest (shortest.html:3)
at shortest (shortest.html:3)
at shortest (shortest.html:3)
at shortest (shortest.html:3)
at shortest (shortest.html:3)
at shortest (shortest.html:3)
at shortest (shortest.html:3)
at shortest (shortest.html:3)This kind of bug is called a stack overflow. (This is where the popular website https://stackoverflow.com got its name.) The constant function calls with no returns grow the call stack until all the computer’s memory allocated for the call stack is used up. To prevent this, the Python and JavaScript interpreters crash the program after a certain limit of function calls that don’t return a value.
This limit is called the maximum recursion depth or maximum call stack size. For Python, this is set to 1,000 function calls. For JavaScript, the maximum call stack size depends on the browser running the code but is generally at least 10,000 or so. Think of a stack overflow as happening when the call stack gets “too high” (that is, consumes too much computer memory), as in Figure 1-8.
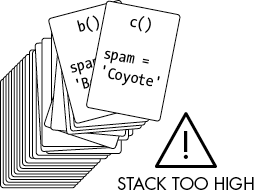
Figure 1-8: A stack overflow happens when the call stack becomes too high, with too many frame objects taking up the computer’s memory.
Stack overflows don’t damage the computer. The computer just detects that the limit of function calls without returns has been reached and terminates the program. At worst, you’ll lose any unsaved work the program had. Stack overflows can be prevented by having something called a base case, which is explained next.
The stack overflow example has a shortest() function that calls shortest() but never returns. To avoid a crash, there needs to be a case, or set of circumstances, where the function stops calling itself and instead just returns. This is called a base case. By contrast, a case where the function recursively calls itself is called a recursive case.
All recursive functions require at least one base case and at least one recursive case. If there is no base case, the function never stops making recursive calls and eventually causes a stack overflow. If there is no recursive case, the function never calls itself and is an ordinary function, not a recursive one. When you start writing your own recursive functions, a good first step is to figure out what the base case and recursive case should be.
Take a look at this shortestWithBaseCase.py program, which defines the shortest recursive function that won’t crash from a stack overflow:
Python
def shortestWithBaseCase(makeRecursiveCall):
print('shortestWithBaseCase(%s) called.' % makeRecursiveCall)
if not makeRecursiveCall:
# BASE CASE
print('Returning from base case.')
❶ return
else:
# RECURSIVE CASE
❷ shortestWithBaseCase(False)
print('Returning from recursive case.')
return
print('Calling shortestWithBaseCase(False):')
❸ shortestWithBaseCase(False)
print()
print('Calling shortestWithBaseCase(True):')
❹ shortestWithBaseCase(True)This code is equivalent to the following shortestWithBaseCase.html program:
JavaScript
<script type="text/javascript">
function shortestWithBaseCase(makeRecursiveCall) {
document.write("shortestWithBaseCase(" + makeRecursiveCall +
") called.<br />");
if (makeRecursiveCall === false) {
// BASE CASE
document.write("Returning from base case.<br />");
❶ return;
} else {
// RECURSIVE CASE
❷ shortestWithBaseCase(false);
document.write("Returning from recursive case.<br />");
return;
}
}
document.write("Calling shortestWithBaseCase(false):<br />");
❸ shortestWithBaseCase(false);
document.write("<br />");
document.write("Calling shortestWithBaseCase(true):<br />");
❹ shortestWithBaseCase(true);
</script>When you run this code, the output looks like this:
Calling shortestWithBaseCase(False):
shortestWithBaseCase(False) called.
Returning from base case.
Calling shortestWithBaseCase(True):
shortestWithBaseCase(True) called.
shortestWithBaseCase(False) called.
Returning from base case.
Returning from recursive case.This function doesn’t do anything useful except provide a short example of recursion (and it could be made shorter by removing the text output, but the text is useful for our explanation). When shortestWithBaseCase(False) is called ❸, the base case is executed and the function merely returns ❶. However, when shortestWithBaseCase(True) is called ❹, the recursive case is executed and shortestWithBaseCase(False) is called ❷.
It’s important to note that when shortestWithBaseCase(False) is recursively called from ❷ and then returns, the execution doesn’t immediately move back to the original function call at ❹. The rest of the code in the recursive case after the recursive call still runs, which is why Returning from recursive case. appears in the output. Returning from the base case doesn’t immediately return from all the recursive calls that happened before it. This will be important to keep in mind in the countDownAndUp() example in the next section.
The code in a recursive case can be split into two parts: the code before the recursive call and the code after the recursive call. (If there are two recursive calls in the recursive case, such as with the Fibonacci sequence example in Chapter 2, there will be a before, a between, and an after. But let’s keep it simple for now.)
The important thing to know is that reaching the base case doesn’t necessarily mean reaching the end of the recursive algorithm. It only means the base case won’t continue to make recursive calls.
For example, consider this countDownAndUp.py program whose recursive function counts from any number down to zero, and then back up to the number:
Python
def countDownAndUp(number):
❶ print(number)
if number == 0:
# BASE CASE
❷ print('Reached the base case.')
return
else:
# RECURSIVE CASE
❸ countDownAndUp(number - 1)
❹ print(number, 'returning')
return
❺ countDownAndUp(3)Here is the equivalent countDownAndUp.html program:
JavaScript
<script type="text/javascript">
function countDownAndUp(number) {
❶ document.write(number + "<br />");
if (number === 0) {
// BASE CASE
❷ document.write("Reached the base case.<br />");
return;
} else {
// RECURSIVE CASE
❸ countDownAndUp(number - 1);
❹ document.write(number + " returning<br />");
return;
}
}
❺ countDownAndUp(3);
</script>When you run this code, the output looks like this:
3
2
1
0
Reached the base case.
1 returning
2 returning
3 returningRemember that every time a function is called, a new frame is created and pushed onto the call stack. This frame is where all the local variables and parameters (such as number) are stored. So, there is a separate number variable for each frame on the call stack. This is another often confusing point about recursion: even though, from the source code, it looks like there is only one number variable, remember that because it is a local variable, there is actually a different number variable for each function call.
When countDownAndUp(3) is called ❺, a frame is created, and that frame’s local number variable is set to 3. The function prints the number variable to the screen ❶. As long as number isn’t 0, countDownAndUp() is recursively called with number - 1 ❸. When it calls countDownAndUp(2), a new frame is pushed onto the stack, and that frame’s local number variable is set to 2. Again, the recursive case is reached and calls countDownAndUp(1), which again reaches the recursive case and calls countDownAndUp(0).
This pattern of making consecutive recursive function calls and then returning from the recursive function calls is what causes the countdown of numbers to appear. Once countDownAndUp(0) is called, the base case is reached ❷, and no more recursive calls are made. However, this isn’t the end of our program! When the base case is reached, the local number variable is 0. But when that base case returns, and the frame is popped off the call stack, the frame under it has its own local number variable, with the same 1 value it’s always had. As the execution returns back to the previous frames in the call stack, the code after the recursive call is executed ❹. This is what causes the count up of numbers to appear. Figure 1-9 shows the state of the call stack as countDownAndUp() is recursively called and then returns.
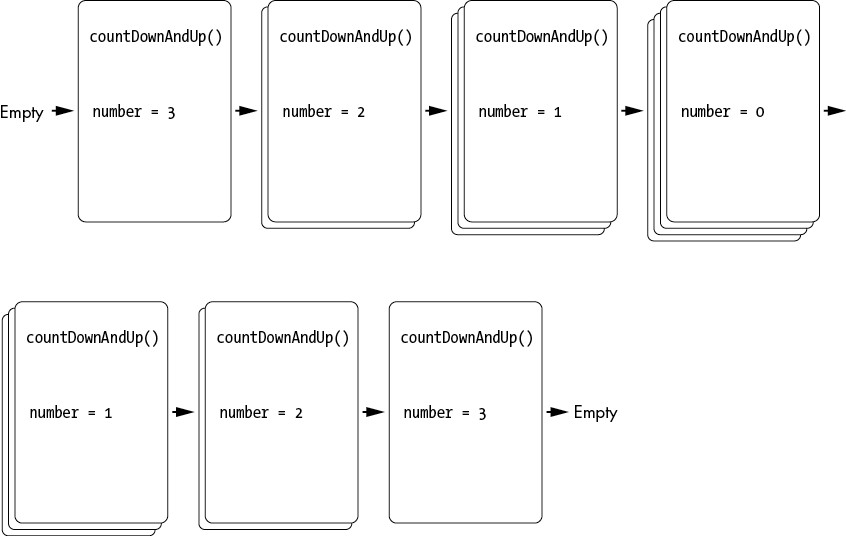
Figure 1-9: The call stack keeping track of the values in the number local variable for each function call
The fact that the code doesn’t stop immediately when the base case is reached will be important to keep in mind for the factorial calculation in the next chapter. Remember, any code after the recursive case will still have to run.
At this point, you might be thinking that the recursive countDownAndUp() function is overengineered and difficult to follow. Why not, instead, use an iterative solution to print numbers? An iterative approach, which uses loops to repeat a task until it’s done, is usually thought of as the opposite of recursion.
Whenever you find yourself asking, “Wouldn’t using a loop be easier?” the answer is almost certainly “Yes,” and you should avoid the recursive solution. Recursion can be tricky for both beginner and experienced programmers, and recursive code isn’t automatically “better” or “more elegant” than iterative code. Readable, easy-to-understand code is more important than any supposed elegance that recursion provides. However, on some occasions an algorithm cleanly maps to a recursive approach. Algorithms that involve tree-like data structures and require backtracking are especially suited for recursion. These ideas are further explored in Chapters 2 and 4.
Recursion often confuses new programmers, but it is built on the simple idea that a function can call itself. Every time a function call is made, a new frame object with information related to the call (such as local variables and a return address for the execution to move to when the function returns) is added to the call stack. The call stack, being a stack data structure, can be altered only by having data added to or removed from its “top.” This is called pushing to and popping from the stack, respectively.
The call stack is handled by the program implicitly, so there is no call stack variable. Calling a function pushes a frame object to the call stack, and returning from a function pops a frame object from the call stack.
Recursive functions have recursive cases, those in which a recursive call is made, and base cases, those where the function simply returns. If there is no base case or a bug prevents a base case from being run, the execution causes a stack overflow that crashes the program.
Recursion is a useful technique, but recursion doesn’t automatically make code “better” or more “elegant.” This idea is explored more in the next chapter.
You can find other introductions to recursion in my 2018 North Bay Python conference talk, “Recursion for Beginners: A Beginner’s Guide to Recursion,” at https://youtu.be/AfBqVVKg4GE. The YouTube channel Computerphile also introduces recursion in its video “What on Earth is Recursion?” at https://youtu.be/Mv9NEXX1VHc. Finally, V. Anton Spraul talks about recursion in his book Think Like a Programmer (No Starch Press, 2012) and in his video “Recursion (Think Like a Programmer)” at https://youtu.be/oKndim5-G94. Wikipedia’s article on recursion goes into great detail at https://en.wikipedia.org/wiki/Recursion.
You can install the ShowCallStack module for Python. This module adds a showcallstack() function that you can place anywhere in your code to see the state of the call stack at that particular point in your program. You can download the module and find instructions for it at https://pypi.org/project/ShowCallStack.
Test your comprehension by answering the following questions: