Check out other books by Al Sweigart, free online or available for purchase:




...and other books as well! Or register for the online video course. You can also donate to support the author directly.





Neither recursion nor iteration is a superior technique in general. In fact, any recursive code can be written as iterative code with a loop and a stack. Recursion doesn’t have some special power enabling it to perform calculations that an iterative algorithm cannot. And any iterative loop can be rewritten as a recursive function.
This chapter compares and contrasts recursion and iteration. We’ll look at the classic Fibonacci and factorial functions and see why their recursive algorithms have critical weaknesses. We’ll also explore the insights a recursive approach can yield by considering an exponent algorithm. Altogether this chapter shines light on the supposed elegance of recursive algorithms and shows when a recursive solution is useful and when it is not.
Many computer science courses use factorial calculation as a classic example of a recursive function. The factorial of an integer (let’s call it n) is the product of all integers from 1 to n. For example, the factorial of 4 is 4 × 3 × 2 × 1, or 24. An exclamation mark is the math notation for factorials, as in 4!, which means the factorial of 4. Table 2-1 shows the first few factorials.
Table 2-1: Factorials of the First Few Integers
| n! | Expanded form | Product | ||
| 1! | = | 1 | = | 1 |
| 2! | = | 1 × 2 | = | 2 |
| 3! | = | 1 × 2 × 3 | = | 6 |
| 4! | = | 1 × 2 × 3 × 4 | = | 24 |
| 5! | = | 1 × 2 × 3 × 4 × 5 | = | 120 |
| 6! | = | 1 × 2 × 3 × 4 × 5 × 6 | = | 720 |
| 7! | = | 1 × 2 × 3 × 4 × 5 × 6 × 7 | = | 5,040 |
| 8! | = | 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 | = | 40,320 |
Factorials are used in all sorts of calculations—for example, finding the number of permutations for something. If you want to know the number of ways that exist to order four people—Alice, Bob, Carol, and David—in a line, the answer is the factorial of 4. Four possible people can be first in line (4); then for each of those four options, three remaining people can be second in line (4 × 3); then two people can be third in line (4 × 3 × 2); and the last person left will be fourth in line (4 × 3 × 2 × 1). The number of ways people can be ordered in line—that is, the number of permutations—is the factorial of the number of people.
Now let’s examine both an iterative and a recursive approach to calculating factorials.
Calculating factorials iteratively is fairly straightforward: multiply the integers 1 up to and including n in a loop. Iterative algorithms always use a loop. A factorialByIteration.py program looks like this:
Python
def factorial(number):
product = 1
for i in range(1, number + 1):
product = product * i
return product
print(factorial(5))And a factorialByIteration.html program looks like this:
JavaScript
<script type="text/javascript">
function factorial(number) {
let product = 1;
for (let i = 1; i <= number; i++) {
product = product * i;
}
return product;
}
document.write(factorial(5));
</script>When you run this code, the output displays the calculation for 5! like this:
120There’s nothing wrong with the iterative solution for calculating factorials; it’s straightforward and gets the job done. But let’s also take a look at the recursive algorithm for insights into the nature of factorials and recursion itself.
Notice that the factorial of 4 is 4 × 3 × 2 × 1, and the factorial of 5 is 5 × 4 × 3 × 2 × 1. So you could say that 5! = 5 × 4!. This is recursive because the definition of the factorial of 5 (or any number n) includes the definition of the factorial of 4 (the number n – 1). In turn, 4! = 4 × 3!, and so on, until you must calculate 1!, the base case, which is simply 1.
The factorialByRecursion.py Python program uses a recursive factorial algorithm:
Python
def factorial(number):
if number == 1:
# BASE CASE
return 1
else:
# RECURSIVE CASE
❶ return number * factorial(number - 1)
print(factorial(5))And the factorialByRecursion.html JavaScript program with equivalent code looks like this:
JavaScript
<script type="text/javascript">
function factorial(number) {
if (number == 1) {
// BASE CASE
return 1;
} else {
// RECURSIVE CASE
❶ return number * factorial(number - 1);
}
}
document.write(factorial(5));
</script>When you run this code to calculate 5! recursively, the output matches the iterative program’s output:
120To many programmers, this recursive code looks strange. You know that factorial(5) must compute 5 × 4 × 3 × 2 × 1, but it’s hard to point to the line of code where this multiplication is taking place.
The confusion arises because the recursive case has one line ❶, half of which is executed before the recursive call and half of which takes place after the recursive call returns. We aren’t used to the idea of only half of a line of code executing at a time.
The first half is factorial(number - 1). This involves calculating number - 1 and making a recursive function call, causing a new frame object to be pushed to the call stack. This happens before the recursive call is made.
The next time the code runs with the old frame object is after factorial(number - 1) has returned. When factorial(5) is called, factorial(number - 1) will be factorial(4), which returns 24. This is when the second half of the line runs. The return number * factorial(number - 1) now looks like return 5 * 24, which is why factorial(5) returns 120.
Figure 2-1 tracks the state of the call stack as frame objects are pushed (which happens as recursive function calls are made) and frame objects are popped (as recursive function calls return). Notice that the multiplication happens after the recursive calls are made, not before.
When the original function call to factorial() returns, it returns the calculated factorial.
The recursive implementation for calculating factorials has a critical weakness. Calculating the factorial of 5 requires five recursive function calls. This means five frame objects are placed on the call stack before the base case is reached. This doesn’t scale.
If you want to calculate the factorial of 1,001, the recursive factorial() function must make 1,001 recursive function calls. However, your program is likely to cause a stack overflow before it can finish, because making so many function calls without returning would exceed the maximum call stack size of the interpreter. This is terrible; you would never want to use a recursive factorial function in real-world code.
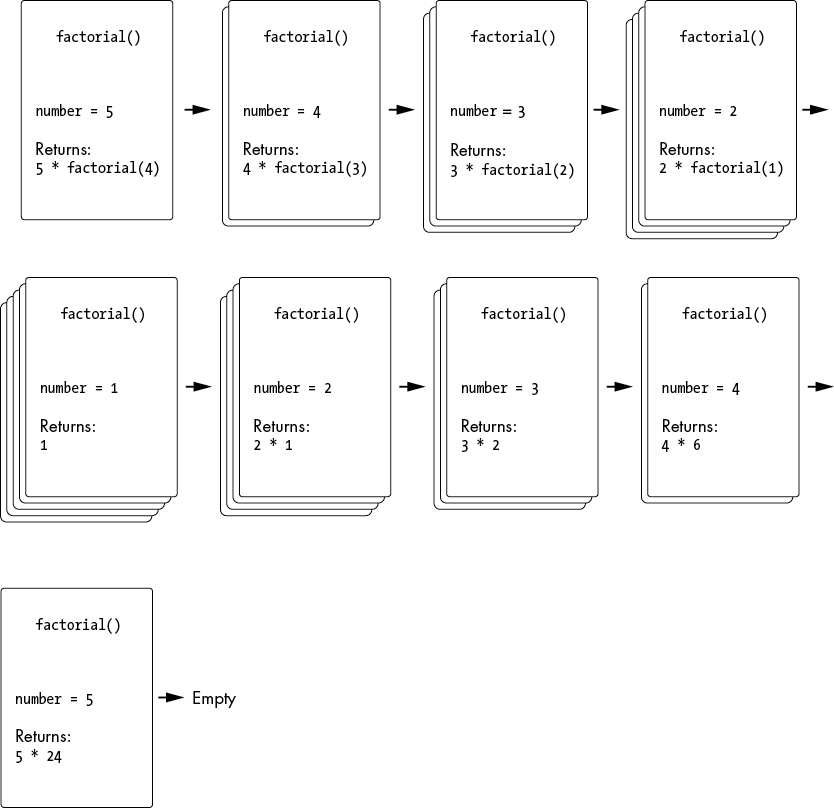
Figure 2-1: The state of the call stack as the recursive calls to factorial() are called and then return
The iterative factorial algorithm, on the other hand, will complete the calculation quickly and efficiently. The stack overflow can be avoided using a technique available in some programming languages called tail call optimization. Chapter 8 covers this topic. However, this technique further complicates the implementation of the recursive function. For calculating factorials, the iterative approach is the simplest and most direct.
The Fibonacci sequence is another classic example for introducing recursion. Mathematically, the Fibonacci sequence of integers begins with the numbers 1 and 1 (or sometimes, 0 and 1). The next number in the sequence is the sum of the previous two numbers. This creates the sequence 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, and so on, forever.
If we call the latest two numbers in the sequence a and b, you can see in Figure 2-2 how the sequence grows.

Figure 2-2: Each number of the Fibonacci sequence is the sum of the previous two numbers.
Let’s explore some code examples of both the iterative and recursive solutions for generating Fibonacci numbers.
The iterative Fibonacci example is straightforward, consisting of a simple for loop and two variables, a and b. This fibonacciByIteration.py Python program implements the iterative Fibonacci algorithm:
Python
def fibonacci(nthNumber):
❶ a, b = 1, 1
print('a = %s, b = %s' % (a, b))
for i in range(2, nthNumber):
❷ a, b = b, a + b # Get the next Fibonacci number.
print('a = %s, b = %s' % (a, b))
return a
print(fibonacci(10))This fibonacciByIteration.html program has the equivalent JavaScript code:
JavaScript
<script type="text/javascript">
function fibonacci(nthNumber) {
❶ let a = 1, b = 1;
let nextNum;
document.write('a = ' + a + ', b = ' + b + '<br />');
for (let i = 2; i < nthNumber; i++) {
❷ nextNum = a + b; // Get the next Fibonacci number.
a = b;
b = nextNum;
document.write('a = ' + a + ', b = ' + b + '<br />');
}
return a;
};
document.write(fibonacci(10));
</script>When you run this code to calculate the 10th Fibonacci number, the output looks like this:
a = 1, b = 1
a = 1, b = 2
a = 2, b = 3
--snip--
a = 34, b = 55
55The program needs to track only the latest two numbers of the sequence at a time. Since the first two numbers in the Fibonacci sequence are defined as 1, we store 1 in variables a and b ❶. Inside the for loop, the next number in the sequence is calculated by adding a and b ❷, which becomes the next value of b, while a obtains the previous value of b. By the time the loop is finished, b contains the nth Fibonacci number, so it is returned.
Calculating Fibonacci numbers involves a recursive property. For example, if you want to calculate the 10th Fibonacci number, you add the ninth and eighth Fibonacci numbers together. To calculate those Fibonacci numbers, you add the eighth and seventh, then the seventh and sixth Fibonacci numbers. A lot of repeat calculations occur: notice that adding the ninth and eighth Fibonacci numbers involves calculating the eighth Fibonacci number again. You continue this recursion until you reach the base case of the first or second Fibonacci number, which is always 1.
The recursive Fibonacci function is in this fibonacciByRecursion.py Python program:
def fibonacci(nthNumber):
print('fibonacci(%s) called.' % (nthNumber))
if nthNumber == 1 or nthNumber == 2: ❶
# BASE CASE
print('Call to fibonacci(%s) returning 1.' % (nthNumber))
return 1
else:
# RECURSIVE CASE
print('Calling fibonacci(%s) and fibonacci(%s).' % (nthNumber - 1, nthNumber - 2))
result = fibonacci(nthNumber - 1) + fibonacci(nthNumber - 2)
print('Call to fibonacci(%s) returning %s.' % (nthNumber, result))
return result
print(fibonacci(10))This fibonacciByRecursion.html file has the equivalent JavaScript program:
<script type="text/javascript">
function fibonacci(nthNumber) {
document.write('fibonacci(' + nthNumber + ') called.<br />');
if (nthNumber === 1 || nthNumber === 2) { ❶
// BASE CASE
document.write('Call to fibonacci(' + nthNumber + ') returning 1.<br />');
return 1;
}
else {
// RECURSIVE CASE
document.write('Calling fibonacci(' + (nthNumber - 1) + ') and fibonacci(' + (nthNumber - 2) + ').<br />');
let result = fibonacci(nthNumber - 1) + fibonacci(nthNumber - 2);
document.write('Call to fibonacci(' + nthNumber + ') returning ' + result + '.<br />');
return result;
}
}
document.write(fibonacci(10) + '<br />');
</script>When you run this code to calculate the 10th Fibonacci number, the output looks like this:
fibonacci(10) called.
Calling fibonacci(9) and fibonacci(8).
fibonacci(9) called.
Calling fibonacci(8) and fibonacci(7).
fibonacci(8) called.
Calling fibonacci(7) and fibonacci(6).
fibonacci(7) called.
--snip--
Call to fibonacci(6) returning 8.
Call to fibonacci(8) returning 21.
Call to fibonacci(10) returning 55.
55Much of the code is for displaying this output, but the fibonacci() function itself is simple. The base case—the circumstances where recursive calls are no longer made—occurs when nthNumber is 1 or 2 ❶. In this case, the function returns 1 since the first and second Fibonacci numbers are always 1. Any other case is a recursive case, so the value that is returned is the sum of fibonacci(nthNumber - 1) and fibonacci(nthNumber - 2). As long as the original nthNumber argument is an integer greater than 0, these recursive calls will eventually reach the base case and stop making more recursive calls.
Remember how the recursive factorial example had a “before the recursive call” and “after the recursive call” part? Because the recursive Fibonacci algorithm makes two recursive calls in its recursive case, you should keep in mind that it has three parts: “before the first recursive call,” “after the first recursive call but before the second recursive call,” and “after the second recursive call.” But the same principles apply. And don’t think that because a base case is reached, no more code remains to run after either recursive call. The recursive algorithm is finished only after the original function call has returned.
You might ask, “Isn’t the iterative Fibonacci solution simpler than the recursive Fibonacci solution?” The answer is “Yes.” Even worse, the recursive solution has a critical inefficiency that is explained in the next section.
Like the recursive factorial algorithm, the recursive Fibonacci algorithm also suffers from a critical weakness: it repeats the same calculations over and over. Figure 2-3 shows how calling fibonacci(6), marked in the tree diagram as fib(6) for brevity, calls fibonacci(5) and fibonacci(4).
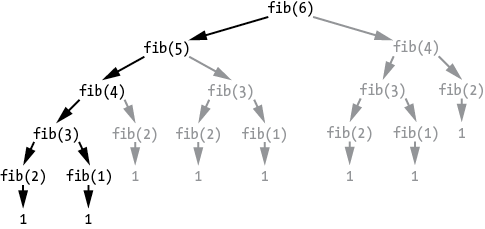
Figure 2-3: A tree diagram of the recursive function calls made starting with fibonacci(6). The redundant function calls are in gray.
This causes a cascade of other function calls until they reach the base cases of fibonacci(2) and fibonacci(1), which return 1. But notice that fibonacci(4) is called twice, and fibonacci(3) is called three times, and so on. This slows the overall algorithm with unnecessarily repeated calculations. This inefficiency gets worse as the Fibonacci number you want to calculate gets larger. While the iterative Fibonacci algorithm can complete fibonacci(100) in less than a second, the recursive algorithm would take over a million years to complete.
Converting a recursive algorithm into an iterative algorithm is always possible. While recursive functions repeat a calculation by calling themselves, this repetition can be performed instead by a loop. Recursive functions also make use of the call stack; however, an iterative algorithm can replace this with a stack data structure. Thus, any recursive algorithm can be performed iteratively by using a loop and a stack.
To demonstrate this, here is factorialEmulateRecursion.py, a Python program that implements an iterative algorithm to emulate a recursive algorithm:
callStack = [] # The explicit call stack, which holds "frame objects". ❶
callStack.append({'returnAddr': 'start', 'number': 5}) # "Call" the "factorial() function". ❷
returnValue = None
while len(callStack) > 0:
# The body of the "factorial() function":
number = callStack[-1]['number'] # Set number parameter.
returnAddr = callStack[-1]['returnAddr']
if returnAddr == 'start':
if number == 1:
# BASE CASE
returnValue = 1
callStack.pop() # "Return" from "function call". ❸
continue
else:
# RECURSIVE CASE
callStack[-1]['returnAddr'] = 'after recursive call'
# "Call" the "factorial() function":
callStack.append({'returnAddr': 'start', 'number': number - 1}) ❹
continue
elif returnAddr == 'after recursive call':
returnValue = number * returnValue
callStack.pop() # "Return from function call". ❺
continue
print(returnValue)The factorialEmulateRecursion.html program holds the equivalent JavaScript:
<script type="text/javascript">
let callStack = []; // The explicit call stack, which holds "frame objects". ❶
callStack.push({"returnAddr": "start", "number": 5}); // "Call" the "factorial() function". ❷
let returnValue;
while (callStack.length > 0) {
// The body of the "factorial() function":
let number = callStack[callStack.length - 1]["number"]; // Set number parameter.
let returnAddr = callStack[callStack.length - 1]["returnAddr"];
if (returnAddr == "start") {
if (number === 1) {
// BASE CASE
returnValue = 1;
callStack.pop(); // "Return" from "function call". ❸
continue;
} else {
// RECURSIVE CASE
callStack[callStack.length - 1]["returnAddr"] = "after recursive call";
// "Call" the "factorial() function":
callStack.push({"returnAddr": "start", "number": number - 1}); ❹
continue;
}
} else if (returnAddr == "after recursive call") {
returnValue = number * returnValue;
callStack.pop(); // "Return from function call". ❺
continue;
}
}
document.write(returnValue + "<br />");
</script> Notice that this program doesn’t have a recursive function; it doesn’t have any functions at all! The program emulates recursive function calls by using a list as a stack data structure (stored in the callStack variable ❶) to mimic the call stack. A dictionary storing the return address information and nthNumber local variable emulates a frame object ❷. The program emulates function calls by pushing these frame objects onto the call stack ❹, and it emulates returning from a function call by popping frame objects off the call stack 35.
Any recursive function can be written iteratively this way. Although this code is incredibly difficult to understand and you’d never write a real-world factorial algorithm this way, it does demonstrate that recursion has no innate capability that iterative code does not have.
Likewise, converting an iterative algorithm into a recursive algorithm is always possible. An iterative algorithm is simply code that uses a loop. The code that is repeatedly executed (the loop’s body) can be placed in a recursive function’s body. And just as the code in the loop’s body is executed repeatedly, we need to repeatedly call the function to execute its code. We can do this by calling the function from the function itself, creating a recursive function.
The Python code in hello.py demonstrates printing Hello, world! five times by using a loop and then also using a recursive function:
Python
print('Code in a loop:')
i = 0
while i < 5:
print(i, 'Hello, world!')
i = i + 1
print('Code in a function:')
def hello(i=0):
print(i, 'Hello, world!')
i = i + 1
if i < 5:
hello(i) # RECURSIVE CASE
else:
return # BASE CASE
hello()The equivalent JavaScript code is in hello.html:
JavaScript
<script type="text/javascript">
document.write("Code in a loop:<br />");
let i = 0;
while (i < 5) {
document.write(i + " Hello, world!<br />");
i = i + 1;
}
document.write("Code in a function:<br />");
function hello(i) {
if (i === undefined) {
i = 0; // i defaults to 0 if unspecified.
}
document.write(i + " Hello, world!<br />");
i = i + 1;
if (i < 5) {
hello(i); // RECURSIVE CASE
}
else {
return; // BASE CASE
}
}
hello();
</script>The output of these programs looks like this:
Code in a loop:
0 Hello, world!
1 Hello, world!
2 Hello, world!
3 Hello, world!
4 Hello, world!
Code in a function:
0 Hello, world!
1 Hello, world!
2 Hello, world!
3 Hello, world!
4 Hello, world!The while loop has a condition, i < 5, that determines whether the program keeps looping. Similarly, the recursive function uses this condition for its recursive case, which causes the function to call itself and execute the Hello, world! to display its code again.
For a more real-world example, the following are iterative and recursive functions that return the index of a substring, needle, in a string, haystack. The functions return -1 if the substring isn’t found. This is similar to Python’s find() string method and JavaScript’s indexOf() string method. This findSubstring.py program has a Python version:
Python
def findSubstringIterative(needle, haystack):
i = 0
while i < len(haystack):
if haystack[i:i + len(needle)] == needle:
return i # Needle found.
i = i + 1
return -1 # Needle not found.
def findSubstringRecursive(needle, haystack, i=0):
if i >= len(haystack):
return -1 # BASE CASE (Needle not found.)
if haystack[i:i + len(needle)] == needle:
return i # BASE CASE (Needle found.)
else:
# RECURSIVE CASE
return findSubstringRecursive(needle, haystack, i + 1)
print(findSubstringIterative('cat', 'My cat Zophie'))
print(findSubstringRecursive('cat', 'My cat Zophie'))This findSubstring.html program has the equivalent JavaScript version:
JavaScript
<script type="text/javascript">
function findSubstringIterative(needle, haystack) {
let i = 0;
while (i < haystack.length) {
if (haystack.substring(i, i + needle.length) == needle) {
return i; // Needle found.
}
i = i + 1
}
return -1; // Needle not found.
}
function findSubstringRecursive(needle, haystack, i) {
if (i === undefined) {
i = 0;
}
if (i >= haystack.length) {
return -1; // # BASE CASE (Needle not found.)
}
if (haystack.substring(i, i + needle.length) == needle) {
return i; // # BASE CASE (Needle found.)
} else {
// RECURSIVE CASE
return findSubstringRecursive(needle, haystack, i + 1);
}
}
document.write(findSubstringIterative("cat", "My cat Zophie") + "<br />");
document.write(findSubstringRecursive("cat", "My cat Zophie") + "<br />");
</script>These programs make a call to findSubstringIterative() and findSubstringRecursive(), which return 3 because that is the index where cat is found in My cat Zophie:
3
3The programs in this section demonstrate that it is always possible to turn any loop into an equivalent recursive function. While replacing a loop with recursion is possible, I advise against it. This is doing recursion for recursion’s sake, and since recursion is often harder to understand than iterative code, code readability deteriorates.
Although recursion doesn’t necessarily produce better code, taking a recursive approach can give you new insights into your programming problem. As a case study, let’s examine how to calculate exponents.
Exponents are calculated by multiplying a number by itself. For example, the exponent “three raised to the sixth power,” or 36, is equal to multiplying 3 by itself six times: 3 × 3 × 3 × 3 × 3 × 3 = 729. This is such a common operation that Python has the ** operator and JavaScript has the built-in Math.pow() function to perform exponentiation. We can calculate 36 with the Python code 3 ** 6 and with the JavaScript code Math.pow(3, 6).
But let’s write our own exponent-calculating code. The solution is straightforward: create a loop that repeatedly multiplies a number by itself and returns the final product. Here is an iterative exponentByIteration.py Python program:
Python
def exponentByIteration(a, n):
result = 1
for i in range(n):
result *= a
return result
print(exponentByIteration(3, 6))
print(exponentByIteration(10, 3))
print(exponentByIteration(17, 10))And here is an equivalent JavaScript exponentByIteration.html program:
JavaScript
<script type="text/javascript">
function exponentByIteration(a, n) {
let result = 1;
for (let i = 0; i < n; i++) {
result *= a;
}
return result;
}
document.write(exponentByIteration(3, 6) + "<br />");
document.write(exponentByIteration(10, 3) + "<br />");
document.write(exponentByIteration(17, 10) + "<br />");
</script>When you run these programs, the output looks like this:
729
1000
2015993900449This is a straightforward calculation that we can easily write with a loop. The downside to using a loop is that the function slows as the exponents get larger: calculating 312 takes twice as long as 36, and 3600 takes one hundred times as long as 36. In the next section, we address this by thinking recursively.
Let’s think of what a recursive solution for the exponentiation of, say, 36 would be. Because of the associative property of multiplication, 3 × 3 × 3 × 3 × 3 × 3 is the same as (3 × 3 × 3) × (3 × 3 × 3), which is the same as (3 × 3 × 3)2. And since (3 × 3 × 3) is the same as 33, we can determine that 36 is the same as (33)2. This is an example of what mathematics calls the power rule: (am)n = amn. Mathematics also gives us the product rule: an × am = an + m, including an × a = an + 1.
We can use these mathematical rules to make an exponentByRecursion() function. If exponentByRecursion(3, 6) is called, it’s the same as exponentByRecursion(3, 3) * exponentByRecursion(3, 3). Of course, we don’t actually have to make both exponentByRecursion(3, 3) calls: we could just save the return value to a variable and multiply it by itself.
That works for even-numbered exponents, but what about for odd-numbered exponents? If we had to calculate 37, or 3 × 3 × 3 × 3 × 3 × 3 × 3, this is the same as (3 × 3 × 3 × 3 × 3 × 3) × 3, or (36) × 3. Then we can make the same recursive call to calculate 36.
Those are the recursive cases, but what are the base cases? Mathematically speaking, any number to the zeroth power is defined as 1, while any number to the first power is the number itself. So for any function call exponentByRecursion(a, n), if n is 0 or 1, we can simply return 1 or a, respectively, because a0 is always 1 and a1 is always a.
Using all this information, we can write code for the exponentByRecursion() function. Here is an exponentByRecursion.py file with the Python code:
Python
def exponentByRecursion(a, n):
if n == 1:
# BASE CASE
return a
elif n % 2 == 0:
# RECURSIVE CASE (When n is even.)
result = exponentByRecursion(a, n // 2)
return result * result
elif n % 2 == 1:
# RECURSIVE CASE (When n is odd.)
result = exponentByRecursion(a, n // 2)
return result * result * a
print(exponentByRecursion(3, 6))
print(exponentByRecursion(10, 3))
print(exponentByRecursion(17, 10))And here is the equivalent JavaScript code in exponentByRecursion.html:
JavaScript
<script type="text/javascript">
function exponentByRecursion(a, n) {
if (n === 1) {
// BASE CASE
return a;
} else if (n % 2 === 0) {
// RECURSIVE CASE (When n is even.)
result = exponentByRecursion(a, n / 2);
return result * result;
} else if (n % 2 === 1) {
// RECURSIVE CASE (When n is odd.)
result = exponentByRecursion(a, Math.floor(n / 2));
return result * result * a;
}
}
document.write(exponentByRecursion(3, 6));
document.write(exponentByRecursion(10, 3));
document.write(exponentByRecursion(17, 10));
</script>When you run this code, the output is identical to the iterative version:
729
1000
2015993900449Each recursive call effectively cuts the problem size in half. This is what makes our recursive exponent algorithm faster than the iterative version; calculating 31000 iteratively entails 1,000 multiplication operations, while doing it recursively requires only 23 multiplications and divisions. When running the Python code under a performance profiler, calculating 31000 iteratively 100,000 times takes 10.633 seconds, but the recursive calculation takes only 0.406 seconds. That is a huge improvement!
Our original iterative exponents function took a straightforward approach: loop the same number of times as the exponent power. However, this doesn’t scale well for larger powers. Our recursive implementation forced us to think about how to break this problem into smaller subproblems. This approach turns out to be much more efficient.
Because every recursive algorithm has an equivalent iterative algorithm, we could make a new iterative exponents function based on the power rule that the recursive algorithm uses. The following exponentWithPowerRule.py program has such a function:
Python
def exponentWithPowerRule(a, n):
# Step 1: Determine the operations to be performed.
opStack = []
while n > 1:
if n % 2 == 0:
# n is even.
opStack.append('square')
n = n // 2
elif n % 2 == 1:
# n is odd.
n -= 1
opStack.append('multiply')
# Step 2: Perform the operations in reverse order.
result = a # Start result at `a`.
while opStack:
op = opStack.pop()
if op == 'multiply':
result *= a
elif op == 'square':
result *= result
return result
print(exponentWithPowerRule(3, 6))
print(exponentWithPowerRule(10, 3))
print(exponentWithPowerRule(17, 10))Here is the equivalent JavaScript program in exponentWithPowerRule.html:
JavaScript
<script type="text/javascript">
function exponentWithPowerRule(a, n) {
// Step 1: Determine the operations to be performed.
let opStack = [];
while (n > 1) {
if (n % 2 === 0) {
// n is even.
opStack.push("square");
n = Math.floor(n / 2);
} else if (n % 2 === 1) {
// n is odd.
n -= 1;
opStack.push("multiply");
}
}
// Step 2: Perform the operations in reverse order.
let result = a; // Start result at `a`.
while (opStack.length > 0) {
let op = opStack.pop();
if (op === "multiply") {
result = result * a;
} else if (op === "square") {
result = result * result;
}
}
return result;
}
document.write(exponentWithPowerRule(3, 6) + "<br />");
document.write(exponentWithPowerRule(10, 3) + "<br />");
document.write(exponentWithPowerRule(17, 10) + "<br />");
</script>Our algorithm keeps reducing n by dividing it in half (if it’s even) or subtracting 1 (if it’s odd) until it is 1. This gives us the squaring or multiply-by-a operations we have to perform. After finishing this step, we perform these operations in reverse order. A generic stack data structure (separate from the call stack) is useful for reversing the order of these operations since it’s a first-in, last-out data structure. The first step pushes squaring or multiply-by-a operations to a stack in the opStack variable. In the second step, it performs these operations as it pops them off the stack.
For example, calling exponentWithPowerRule(6, 5) to calculate 65 sets a as 6 and n as 5. The function notes that n is odd. This means we should subtract 1 from n to get 4 and push a multiply-by-a operation to opStack. Now that n is 4 (even), we divide it by 2 to get 2 and push a squaring operation to opStack. Since n is now 2 and even again, we divide it by 2 to get 1 and push another squaring operation to opStack. Now that n is 1, we are finished with this first step.
To perform the second step, we start the result as a (which is 6). We pop the opStack stack to get a squaring operation, telling the program to set result to result * result (that is, result2) or 36. We pop the next operation off opStack, and it is another squaring operation, so the program changes the 36 in result to 36 * 36, or 1296. We pop the last operation off opStack, and it is a multiply-by-a operation, so we multiply the 1296 in result by a (which is 6) to get 7776. There are no more operations on opStack, so the function is now finished. When we double-check our math, we find that 65 is indeed 7,776.
The stack in opStack looks like Figure 2-4 as the function call exponentWithPowerRule(6, 5) executes.
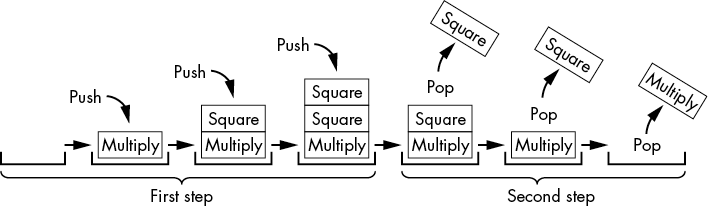
Figure 2-4: The stack in opStack during the exponentWithPowerRule(6, 5) function call
When you run this code, the output is identical to the other exponent programs:
729
1000
2015993900449The iterative exponents function that uses the power rule has the improved performance of the recursive algorithm, while not suffering from the risk of a stack overflow. We might not have thought of this new, improved iterative algorithm without the insights of recursive thinking.
You never need to use recursion. No programming problem requires recursion. This chapter has shown that recursion has no magical power to do things that iterative code in a loop with a stack data structure cannot do. In fact, a recursive function might be an overcomplicated solution for what you’re trying to achieve.
However, as the exponent functions we created in the previous section show, recursion can provide new insights into how to think about our programming problem. Three features of a programming problem, when present, make it especially suitable to a recursive approach:
A tree has a self-similar structure: the branching points look similar to the root of a smaller subtree. Recursion often deals with self-similarity and problems that can be divided into smaller, similar subproblems. The root of the tree is analogous to the first call to a recursive function, the branching points are analogous to recursive cases, and the leaves are analogous to the base cases where no more recursive calls are made.
A maze is also a good example of a problem that has a tree-like structure and requires backtracking. In a maze, the branching points occur wherever you must pick one of many paths to follow. If you reach a dead end, you’ve encountered the base case. You must then backtrack to a previous branching point to select a different path to follow.
Figure 2-5 shows a maze’s path visually morphed to look like a biological tree. Despite the visual difference between the maze paths and the tree-shaped paths, their branching points are related to each other in the same way. Mathematically, these graphs are equivalent.
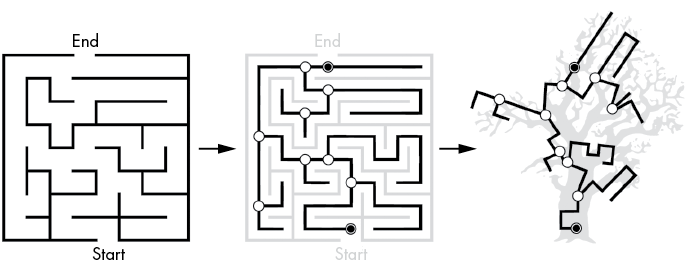
Figure 2-5: A maze (left) along with its interior paths (center) morphed to match a biological tree’s shape (right)
Many programming problems have this tree-like structure at their core. For example, a filesystem has a tree-like structure; the subfolders look like the root folders of a smaller filesystem. Figure 2-6 compares a filesystem to a tree.
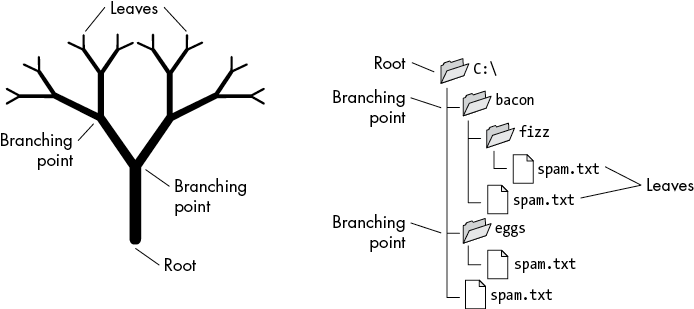
Figure 2-6: A filesystem is similar to a tree structure.
Searching for a specific filename in a folder is a recursive problem: you search the folder and then recursively search the folder’s subfolders. Folders with no subfolders are the base cases that cause the recursive searching to stop. If your recursive algorithm doesn’t find the filename it’s looking for, it backtracks to a previous parent folder and continues searching from there.
The third point is a matter of practicality. If your tree structure has so many levels of branches that a recursive function would cause a stack overflow before it can reach the leaves, then recursion isn’t a suitable solution.
On the other hand, recursion is the best approach for creating programming language compilers. Compiler design is its own expansive subject and beyond the scope of this book. But programming languages have a set of grammar rules that can break source code into a tree structure similar to the way grammar rules can break English sentences into a tree diagram. Recursion is an ideal technique to apply to compilers.
We’ll identify many recursive algorithms in this book, and they often have the tree-like structure or backtracking features that lend themselves to recursion well.
Hopefully, this chapter has given you a firm idea of how recursive functions compare to the iterative algorithms you’re likely more familiar with. The rest of this book dives into the details of various recursive algorithms. But how should you go about writing your own recursive functions?
The first step is always to identify the recursive case and the base case. You can take a top-down approach by breaking the problem into subproblems that are similar to the original problem but smaller; this is your recursive case. Then consider when the subproblems are small enough to have a trivial answer; this is your base case. Your recursive function may have more than one recursive case or base case, but all recursive functions will always have at least one recursive case and at least one base case.
The recursive Fibonacci algorithm is an example. A Fibonacci number is the sum of the previous two Fibonacci numbers. We can break the problem of finding a Fibonacci number into the subproblems of finding two smaller Fibonacci numbers. We know the first two Fibonacci numbers are both 1, so that provides the base case answer once the subproblems are small enough.
Sometimes it helps to take a bottom-up approach and consider the base case first, and then see how larger and larger problems are constructed and solved from there. The recursive factorial problem is an example. The factorial of 1! is 1. This forms the base case. The next factorial is 2!, and you create it by multiplying 1! by 2. The factorial after that, 3!, is created by multiplying 2! by 3, and so on. From this general pattern, we can figure out what the recursive case for our algorithm will be.
In this chapter, we covered calculating factorials and the Fibonacci sequence, two classic recursive programming problems. This chapter featured both iterative and recursive implementations for these algorithms. Despite being classic examples of recursion, their recursive algorithms suffer from critical flaws. The recursive factorial function can cause stack overflows, while the recursive Fibonacci function performs so many redundant calculations that it’s far too slow to be effective in the real world.
We explored how to create recursive algorithms from iterative algorithms and how to create iterative algorithms from recursive algorithms. Iterative algorithms use a loop, and any recursive algorithm can be performed iteratively by using a loop and a stack data structure. Recursion is often an overly complicated solution, but programming problems that involve a tree-like structure and backtracking are particularly suitable for recursive implementations.
Writing recursive functions is a skill that improves with practice and experience. The rest of this book covers several well-known recursion examples and explores their strengths and limitations.
You can find more information about comparing iteration and recursion in the Computerphile YouTube channel’s video “Programming Loops vs. Recursion” at https://youtu.be/HXNhEYqFo0o. If you want to compare the performance of iterative and recursive functions, you need to learn how to use a profiler. Python profilers are explained in Chapter 13 of my book Beyond the Basic Stuff with Python (No Starch Press, 2020), which can be read at https://inventwithpython.com/beyond/chapter13.html. The official Python documentation also covers profilers at https://docs.python.org/3/library/profile.html. The Firefox profiler for JavaScript is explained on Mozilla’s website at https://developer.mozilla.org/en-US/docs/Tools/Performance. Other browsers have profilers similar to Firefox’s.
Test your comprehension by answering the following questions:
For practice, write a function for each of the following tasks:
1 to n. This is similar to the factorial() function, except it performs addition instead of multiplication. For example, sumSeries(1) returns 1, sumSeries(2) returns 3 (that is, 1 + 2), sumSeries(3) returns 6 (that is, 1 + 2 + 3), and so on. This function should use a loop instead of recursion. Take a look at the factorialByIteration.py program in this chapter for guidance.sumSeries(). This function should use recursive function calls instead of a loop. Look at the factorialByRecursion.py program in this chapter for guidance.n powers of 2 in a function named sumPowersOf2(). The powers of 2 are 2, 4, 8, 16, 32, and so on. In Python, these are calculated with 2 ** 1, 2 ** 2, 2 ** 3, 2 ** 4, 2 ** 5, and so on, respectively. In JavaScript, these are calculated with Math.pow(2, 1), Math.pow(2, 2), and so on. For example, sumPowersOf2(1) returns 2, sumPowersOf2(2) returns 6 (that is, 2 + 4), sumPowersOf2(3) returns 14 (that is, 2 + 4 + 8), and so on.sumPowersOf2(). This function should use recursive function calls instead of a loop.