Check out other books by Al Sweigart, free online or available for purchase:




...and other books as well! Or register for the online video course. You can also donate to support the author directly.





Chapter 4 described a recursive algorithm that solves mazes, but another recursive algorithm generates mazes. In this chapter, we’ll generate mazes in the same format as the maze-solver program in Chapter 4. So, whether you’re a fan of solving mazes or creating them, you’ll now have the power to apply programming to the task.
The algorithm works by visiting a starting space in the maze and then recursively visiting a neighboring space. The maze’s hallways are “carved out” of the maze as the algorithm continues to visit neighbors. If the algorithm reaches a dead end that has no neighboring spaces, it backtracks to earlier spaces until it finds an unvisited neighbor and continues visiting from there. By the time the algorithm backtracks to the starting space, the entire maze has been generated.
The recursive backtracking algorithm we’ll use here produces mazes that tend to have long hallways (the maze spaces that connect branching intersections) and are fairly simple to solve. However, this algorithm is easier to implement than many other maze-generation algorithms, such as Kruskal’s algorithm or Wilson’s algorithm, so it serves as a good introduction to the topic.
Let’s begin by taking a look at the complete Python and JavaScript source code for the program, which uses the recursive backtracking algorithm for maze generation. The rest of this chapter explains each section of code individually.
Copy this Python code to a file named mazeGenerator.py:
Python
import random
WIDTH = 39 # Width of the maze (must be odd).
HEIGHT = 19 # Height of the maze (must be odd).
assert WIDTH % 2 == 1 and WIDTH >= 3
assert HEIGHT % 2 == 1 and HEIGHT >= 3
SEED = 1
random.seed(SEED)
# Use these characters for displaying the maze:
EMPTY = ' '
MARK = '@'
WALL = chr(9608) # Character 9608 is '█'
NORTH, SOUTH, EAST, WEST = 'n', 's', 'e', 'w'
# Create the filled-in maze data structure to start:
maze = {}
for x in range(WIDTH):
for y in range(HEIGHT):
maze[(x, y)] = WALL # Every space is a wall at first.
def printMaze(maze, markX=None, markY=None):
"""Displays the maze data structure in the maze argument. The
markX and markY arguments are coordinates of the current
'@' location of the algorithm as it generates the maze."""
for y in range(HEIGHT):
for x in range(WIDTH):
if markX == x and markY == y:
# Display the '@' mark here:
print(MARK, end='')
else:
# Display the wall or empty space:
print(maze[(x, y)], end='')
print() # Print a newline after printing the row.
def visit(x, y):
""""Carve out" empty spaces in the maze at x, y and then
recursively move to neighboring unvisited spaces. This
function backtracks when the mark has reached a dead end."""
maze[(x, y)] = EMPTY # "Carve out" the space at x, y.
printMaze(maze, x, y) # Display the maze as we generate it.
print('\n\n')
while True:
# Check which neighboring spaces adjacent to
# the mark have not been visited already:
unvisitedNeighbors = []
if y > 1 and (x, y - 2) not in hasVisited:
unvisitedNeighbors.append(NORTH)
if y < HEIGHT - 2 and (x, y + 2) not in hasVisited:
unvisitedNeighbors.append(SOUTH)
if x > 1 and (x - 2, y) not in hasVisited:
unvisitedNeighbors.append(WEST)
if x < WIDTH - 2 and (x + 2, y) not in hasVisited:
unvisitedNeighbors.append(EAST)
if len(unvisitedNeighbors) == 0:
# BASE CASE
# All neighboring spaces have been visited, so this is a
# dead end. Backtrack to an earlier space:
return
else:
# RECURSIVE CASE
# Randomly pick an unvisited neighbor to visit:
nextIntersection = random.choice(unvisitedNeighbors)
# Move the mark to an unvisited neighboring space:
if nextIntersection == NORTH:
nextX = x
nextY = y - 2
maze[(x, y - 1)] = EMPTY # Connecting hallway.
elif nextIntersection == SOUTH:
nextX = x
nextY = y + 2
maze[(x, y + 1)] = EMPTY # Connecting hallway.
elif nextIntersection == WEST:
nextX = x - 2
nextY = y
maze[(x - 1, y)] = EMPTY # Connecting hallway.
elif nextIntersection == EAST:
nextX = x + 2
nextY = y
maze[(x + 1, y)] = EMPTY # Connecting hallway.
hasVisited.append((nextX, nextY)) # Mark as visited.
visit(nextX, nextY) # Recursively visit this space.
# Carve out the paths in the maze data structure:
hasVisited = [(1, 1)] # Start by visiting the top-left corner.
visit(1, 1)
# Display the final resulting maze data structure:
printMaze(maze)Copy this JavaScript code to a file named mazeGenerator.html:
JavaScript
<script type="text/javascript">
const WIDTH = 39; // Width of the maze (must be odd).
const HEIGHT = 19; // Height of the maze (must be odd).
console.assert(WIDTH % 2 == 1 && WIDTH >= 2);
console.assert(HEIGHT % 2 == 1 && HEIGHT >= 2);
// Use these characters for displaying the maze:
const EMPTY = " ";
const MARK = "@";
const WALL = "█"; // Character 9608 is ′█′
const [NORTH, SOUTH, EAST, WEST] = ["n", "s", "e", "w"];
// Create the filled-in maze data structure to start:
let maze = {};
for (let x = 0; x < WIDTH; x++) {
for (let y = 0; y < HEIGHT; y++) {
maze[[x, y]] = WALL; // Every space is a wall at first.
}
}
function printMaze(maze, markX, markY) {
// Displays the maze data structure in the maze argument. The
// markX and markY arguments are coordinates of the current
// '@' location of the algorithm as it generates the maze.
document.write('<code>');
for (let y = 0; y < HEIGHT; y++) {
for (let x = 0; x < WIDTH; x++) {
if (markX === x && markY === y) {
// Display the ′@′ mark here:
document.write(MARK);
} else {
// Display the wall or empty space:
document.write(maze[[x, y]]);
}
}
document.write('<br />'); // Print a newline after printing the row.
}
document.write('</code>');
}
function visit(x, y) {
// "Carve out" empty spaces in the maze at x, y and then
// recursively move to neighboring unvisited spaces. This
// function backtracks when the mark has reached a dead end.
maze[[x, y]] = EMPTY; // "Carve out" the space at x, y.
printMaze(maze, x, y); // Display the maze as we generate it.
document.write('<br /><br /><br />');
while (true) {
// Check which neighboring spaces adjacent to
// the mark have not been visited already:
let unvisitedNeighbors = [];
if (y > 1 && !JSON.stringify(hasVisited).includes(JSON.stringify([x, y - 2]))) {
unvisitedNeighbors.push(NORTH);
}
if (y < HEIGHT - 2 &&
!JSON.stringify(hasVisited).includes(JSON.stringify([x, y + 2]))) {
unvisitedNeighbors.push(SOUTH);
}
if (x > 1 &&
!JSON.stringify(hasVisited).includes(JSON.stringify([x - 2, y]))) {
unvisitedNeighbors.push(WEST);
}
if (x < WIDTH - 2 &&
!JSON.stringify(hasVisited).includes(JSON.stringify([x + 2, y]))) {
unvisitedNeighbors.push(EAST);
}
if (unvisitedNeighbors.length === 0) {
// BASE CASE
// All neighboring spaces have been visited, so this is a
// dead end. Backtrack to an earlier space:
return;
} else {
// RECURSIVE CASE
// Randomly pick an unvisited neighbor to visit:
let nextIntersection = unvisitedNeighbors[
Math.floor(Math.random() * unvisitedNeighbors.length)];
// Move the mark to an unvisited neighboring space:
let nextX, nextY;
if (nextIntersection === NORTH) {
nextX = x;
nextY = y - 2;
maze[[x, y - 1]] = EMPTY; // Connecting hallway.
} else if (nextIntersection === SOUTH) {
nextX = x;
nextY = y + 2;
maze[[x, y + 1]] = EMPTY; // Connecting hallway.
} else if (nextIntersection === WEST) {
nextX = x - 2;
nextY = y;
maze[[x - 1, y]] = EMPTY; // Connecting hallway.
} else if (nextIntersection === EAST) {
nextX = x + 2;
nextY = y;
maze[[x + 1, y]] = EMPTY; // Connecting hallway.
}
hasVisited.push([nextX, nextY]); // Mark space as visited.
visit(nextX, nextY); // Recursively visit this space.
}
}
}
// Carve out the paths in the maze data structure:
let hasVisited = [[1, 1]]; // Start by visiting the top-left corner.
visit(1, 1);
// Display the final resulting maze data structure:
printMaze(maze);
</script>When you run this program, it produces a large amount of text that will fill the terminal window or browser with each step of the maze’s construction. You’ll have to scroll back up to the top to view the entire output.
The maze data structure begins as a completely filled-in 2D space. The recursive backtracker algorithm is given a starting point in this maze and then visits a previously unvisited neighboring space, “carving out” any hallway space in the process. Then it recursively calls itself on a neighboring space it hasn’t visited before. If all the neighboring spaces have already been visited, the algorithm is at a dead end and backtracks to an earlier visited space to visit its unvisited neighbors. The program ends when the algorithm backtracks to its starting location.
You can see this algorithm in action by running the maze-generator program. As the maze is carved out, it displays the current x, y coordinates by using the @ character. The process looks like Figure 11-1. Notice that the fifth image in the top-right corner has backtracked to an earlier space after reaching a dead end to explore a new neighboring direction from that space.
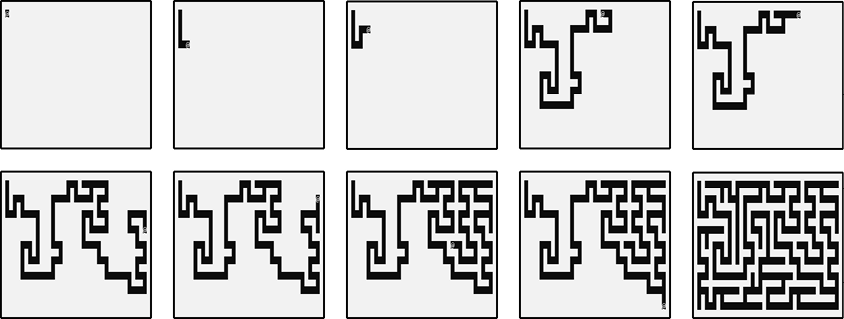
Figure 11-1: The maze as it gets “carved out” by the recursive backtracking algorithm
Let’s take a look at the code in more detail.
The maze generator uses several constants, which we can change before running the program to alter the size and appearance of the maze. The Python code for these constants is as follows:
Python
import random
WIDTH = 39 # Width of the maze (must be odd).
HEIGHT = 19 # Height of the maze (must be odd).
assert WIDTH % 2 == 1 and WIDTH >= 3
assert HEIGHT % 2 == 1 and HEIGHT >= 3
SEED = 1
random.seed(SEED)The JavaScript code is as follows:
JavaScript
<script type="text/javascript">
const WIDTH = 39; // Width of the maze (must be odd).
const HEIGHT = 19; // Height of the maze (must be odd).
console.assert(WIDTH % 2 == 1 && WIDTH >= 3);
console.assert(HEIGHT % 2 == 1 && HEIGHT >= 3);The constants WIDTH and HEIGHT dictate the size of the maze. They must be odd numbers, because our maze data structure requires walls between the visited spaces of the maze, leaving us with odd-numbered dimensions. To make sure the WIDTH and HEIGHT constants are set correctly, we use assertions to stop the program if the constants aren’t odd or are too small.
The program relies on a random seed value to reproduce the same maze, given the same seed value. The Python version of this program lets us set this value by calling the random.seed() function. Unfortunately, JavaScript doesn’t have a way to set the seed value explicitly and will generate different mazes each time we run the program.
The Python code continues by setting a few more constants:
Python
# Use these characters for displaying the maze:
EMPTY = ' '
MARK = '@'
WALL = chr(9608) # Character 9608 is '█'
NORTH, SOUTH, EAST, WEST = 'n', 's', 'e', 'w'The JavaScript code for these constants is as follows:
JavaScript
// Use these characters for displaying the maze:
const EMPTY = " ";
const MARK = "@";
const WALL = "█"; // Character 9608 is ′█′
const [NORTH, SOUTH, EAST, WEST] = ["n", "s", "e", "w"];The EMPTY and WALL constants affect how the maze is displayed on the screen. The MARK constant is used to point out the position of the algorithm in the maze as it runs. The NORTH, SOUTH, EAST, and WEST constants represent the directions that the mark can move through the maze and are used to make the code more readable.
The maze data structure is a Python dictionary or JavaScript object that has keys of Python tuples or JavaScript arrays of the x, y coordinates of every space in the maze. The value for these keys is a string in the WALL or EMPTY constant. This string notes whether this space is a blocking wall or a passable empty space in the maze.
For example, the maze in Figure 11-2 is represented by the following data structure:
{(0, 0): '█', (0, 1): '█', (0, 2): '█', (0, 3): '█', (0, 4): '█',
(0, 5): '█', (0, 6): '█', (1, 0): '█', (1, 1): ' ', (1, 2): ' ',
(1, 3): ' ', (1, 4): ' ', (1, 5): ' ', (1, 6): '█', (2, 0): '█',
(2, 1): '█', (2, 2): '█', (2, 3): '█', (2, 4): '█', (2, 5): ' ',
(2, 6): '█', (3, 0): '█', (3, 1): ' ', (3, 2): '█', (3, 3): ' ',
(3, 4): ' ', (3, 5): ' ', (3, 6): '█', (4, 0): '█', (4, 1): ' ',
(4, 2): '█', (4, 3): ' ', (4, 4): '█', (4, 5): '█', (4, 6): '█',
(5, 0): '█', (5, 1): ' ', (5, 2): ' ', (5, 3): ' ', (5, 4): ' ',
(5, 5): ' ', (5, 6): '█', (6, 0): '█', (6, 1): '█', (6, 2): '█',
(6, 3): '█', (6, 4): '█', (6, 5): '█', (6, 6): '█'}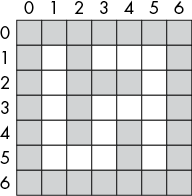
Figure 11-2: An example maze that can be represented by a data structure
The program must start with every space set to WALL. The recursive visit() function then carves out the hallways and intersections of the maze by setting spaces to EMPTY:
Python
# Create the filled-in maze data structure to start:
maze = {}
for x in range(WIDTH):
for y in range(HEIGHT):
maze[(x, y)] = WALL # Every space is a wall at first.The corresponding JavaScript code is as follows:
JavaScript
// Create the filled-in maze data structure to start:
let maze = {};
for (let x = 0; x < WIDTH; x++) {
for (let y = 0; y < HEIGHT; y++) {
maze[[x, y]] = WALL; // Every space is a wall at first.
}
}We create the blank dictionary (in Python) or object (in JavaScript) in the maze global variable. The for loops loop over every possible x, y coordinate, setting each to WALL to create a completely filled-in maze. The call to visit() will carve out the hallways of the maze from this data structure by setting the spaces in it to EMPTY.
To represent the maze as a data structure, the Python program uses a dictionary, and the JavaScript program uses an object. Within this structure, the keys are lists or arrays of two integers for the x- and y-coordinates, while the value is either the WALL or EMPTY single-character strings. Thus, we can access the wall or empty hallway space at the coordinates x, y in the maze as maze[(x, y)] in Python code and as maze[[x, y]] in JavaScript code.
The Python code for printMaze() starts as follows:
Python
def printMaze(maze, markX=None, markY=None):
"""Displays the maze data structure in the maze argument. The
markX and markY arguments are coordinates of the current
'@' location of the algorithm as it generates the maze."""
for y in range(HEIGHT):
for x in range(WIDTH):The JavaScript code for printMaze() starts as follows:
JavaScript
function printMaze(maze, markX, markY) {
// Displays the maze data structure in the maze argument. The
// markX and markY arguments are coordinates of the current
// '@' location of the algorithm as it generates the maze.
document.write('<code>');
for (let y = 0; y < HEIGHT; y++) {
for (let x = 0; x < WIDTH; x++) {The printMaze() function prints the maze data structure it’s passed as the maze parameter on the screen. Optionally, if markX and markY integer arguments are passed, the MARK constant (which we set to @) appears at these x, y coordinates in the printed maze. To make sure the maze is printed in a monospace font, the JavaScript version writes the HTML tag <code> before printing the maze itself. Without this HTML tag, the maze will appear distorted in the browser.
Within the function, nested for loops loop over every space in the maze data structure. These for loops iterate over each y-coordinate from 0 up to, but not including, HEIGHT, and each x-coordinate from 0 up to, but not including, WIDTH.
Inside the inner for loop, if the current x, y coordinates match the position of the mark (the location where the algorithm is currently carving), the program displays the @ in the MARK constant. The Python code does this as follows:
Python
if markX == x and markY == y:
# Display the '@' mark here:
print(MARK, end='')
else:
# Display the wall or empty space:
print(maze[(x, y)], end='')
print() # Print a newline after printing the row.The JavaScript code is as follows:
JavaScript
if (markX === x && markY === y) {
// Display the ′@′ mark here:
document.write(MARK);
} else {
// Display the wall or empty space:
document.write(maze[[x, y]]);
}
}
document.write('<br />'); // Print a newline after printing the row.
}
document.write('</code>');
}Otherwise, the program displays either the WALL or EMPTY constant’s character at this x, y coordinate in the maze data structure by printing maze[(x, y)] in Python and maze[[x, y]] in JavaScript. After the inner for loop is done looping over the x-coordinates, we print a newline at the end of the row in preparation for the next row.
The visit() function implements the recursive backtracker algorithm. The function has a list (in Python) or array (in JavaScript) that keeps track of the x, y coordinates that have already been visited by previous visit() function calls. It also in-place modifies the global maze variable that stores the maze data structure. The Python code for visit() begins as follows:
Python
def visit(x, y):
""""Carve out" empty spaces in the maze at x, y and then
recursively move to neighboring unvisited spaces. This
function backtracks when the mark has reached a dead end."""
maze[(x, y)] = EMPTY # "Carve out" the space at x, y.
printMaze(maze, x, y) # Display the maze as we generate it.
print('\n\n')The JavaScript code for visit() begins as follows:
JavaScript
function visit(x, y) {
// "Carve out" empty spaces in the maze at x, y and then
// recursively move to neighboring unvisited spaces. This
// function backtracks when the mark has reached a dead end.
maze[[x, y]] = EMPTY; // "Carve out" the space at x, y.
printMaze(maze, x, y); // Display the maze as we generate it.
document.write('<br /><br /><br />');The visit() function accepts x, y coordinates as arguments for the place in the maze the algorithm is visiting. Then the function changes the data structure in maze at this location to an empty space. To let the user see the progression of the maze generation, it calls printMaze(), passing the x and y arguments as the current position of the mark.
Next, the recursive backtracker calls visit() with the coordinates of a previously unvisited neighboring space. The Python code continues as follows:
Python
while True:
# Check which neighboring spaces adjacent to
# the mark have not been visited already:
unvisitedNeighbors = []
if y > 1 and (x, y - 2) not in hasVisited:
unvisitedNeighbors.append(NORTH)
if y < HEIGHT - 2 and (x, y + 2) not in hasVisited:
unvisitedNeighbors.append(SOUTH)
if x > 1 and (x - 2, y) not in hasVisited:
unvisitedNeighbors.append(WEST)
if x < WIDTH - 2 and (x + 2, y) not in hasVisited:
unvisitedNeighbors.append(EAST)The JavaScript code continues as follows:
while (true) {
// Check which neighboring spaces adjacent to
// the mark have not been visited already:
let unvisitedNeighbors = [];
if (y > 1 && !JSON.stringify(hasVisited).includes(JSON.stringify([x, y - 2]))) {
unvisitedNeighbors.push(NORTH);
}
if (y < HEIGHT - 2 && !JSON.stringify(hasVisited).includes(JSON.stringify([x, y + 2]))) {
unvisitedNeighbors.push(SOUTH);
}
if (x > 1 && !JSON.stringify(hasVisited).includes(JSON.stringify([x - 2, y]))) {
unvisitedNeighbors.push(WEST);
}
if (x < WIDTH - 2 && !JSON.stringify(hasVisited).includes(JSON.stringify([x + 2, y]))) {
unvisitedNeighbors.push(EAST);
}The while loop continues to loop as long as unvisited neighbors remain for this location in the maze. We create a list or array of unvisited neighboring spaces in the unvisitedNeighbors variables. Four if statements check that the current x, y position is not on the border of the maze (so that we still have a neighboring space to check) and whether the neighboring space’s x, y coordinates don’t appear in the hasVisited list or array already.
If all the neighbors have been visited, the function returns so that it can backtrack to an earlier space. The Python code continues on to check for the base case:
Python
if len(unvisitedNeighbors) == 0:
# BASE CASE
# All neighboring spaces have been visited, so this is a
# dead end. Backtrack to an earlier space:
returnThe JavaScript code does so as follows:
JavaScript
if (unvisitedNeighbors.length === 0) {
// BASE CASE
// All neighboring spaces have been visited, so this is a
// dead end. Backtrack to an earlier space:
return;The base case for the recursive backtracking algorithm occurs when no unvisited neighbors remain to visit next. In this case, the function simply returns. The visit() function itself has no return value. Rather, the recursive function calls visit() to modify the maze data structure in the global maze variable as a side effect. When the original function call to maze() returns, the maze global variable contains the completely generated maze.
The Python code continues on to the recursive case like this:
Python
else:
# RECURSIVE CASE
# Randomly pick an unvisited neighbor to visit:
nextIntersection = random.choice(unvisitedNeighbors)
# Move the mark to an unvisited neighboring space:
if nextIntersection == NORTH:
nextX = x
nextY = y - 2
maze[(x, y - 1)] = EMPTY # Connecting hallway.
elif nextIntersection == SOUTH:
nextX = x
nextY = y + 2
maze[(x, y + 1)] = EMPTY # Connecting hallway.
elif nextIntersection == WEST:
nextX = x - 2
nextY = y
maze[(x - 1, y)] = EMPTY # Connecting hallway.
elif nextIntersection == EAST:
nextX = x + 2
nextY = y
maze[(x + 1, y)] = EMPTY # Connecting hallway.
hasVisited.append((nextX, nextY)) # Mark space as visited.
visit(nextX, nextY) # Recursively visit this space.The JavaScript code continues as follows:
JavaScript
} else {
// RECURSIVE CASE
// Randomly pick an unvisited neighbor to visit:
let nextIntersection = unvisitedNeighbors[
Math.floor(Math.random() * unvisitedNeighbors.length)];
// Move the mark to an unvisited neighboring space:
let nextX, nextY;
if (nextIntersection === NORTH) {
nextX = x;
nextY = y - 2;
maze[[x, y - 1]] = EMPTY; // Connecting hallway.
} else if (nextIntersection === SOUTH) {
nextX = x;
nextY = y + 2;
maze[[x, y + 1]] = EMPTY; // Connecting hallway.
} else if (nextIntersection === WEST) {
nextX = x - 2;
nextY = y;
maze[[x - 1, y]] = EMPTY; // Connecting hallway.
} else if (nextIntersection === EAST) {
nextX = x + 2;
nextY = y;
maze[[x + 1, y]] = EMPTY; // Connecting hallway.
}
hasVisited.push([nextX, nextY]); // Mark space as visited.
visit(nextX, nextY); // Recursively visit this space.
}
}
}The unvisitedNeighbors list or array contains one or more of the NORTH, SOUTH, WEST, and EAST constants. We choose one of these directions for the next recursive call to visit(), and then set the nextX and nextY variables with the coordinates of the neighboring space in this direction.
After this, we add the x, y coordinates of nextX and nextY to the hasVisited list or array before making the recursive call for this neighboring space. In this way, the visit() function continues to visit neighboring spaces, carving out the maze hallways by setting locations in maze to EMPTY. The connecting hallway between the current space and neighboring space is also set to EMPTY.
When no neighbors exist, the base case simply returns to an earlier location. In the visit() function, the execution jumps back to the start of the while loop. The code in the while loop again checks which neighboring spaces haven’t been visited and makes a recursive visit() call on one of them, or returns if all neighboring spaces have already been visited.
As the maze fills up with hallways and each space has been visited, the recursive calls will continue to return until the original visit() function call returns. At this point, the maze variable contains the completely generated maze.
The recursive visit() uses two global variables, maze and hasVisited. The hasVisited variable is a list or array containing the x, y coordinates of every space the algorithm has visited and begins with (1, 1) since that is the maze starting point. The Python code for this is as follows:
Python
# Carve out the paths in the maze data structure:
hasVisited = [(1, 1)] # Start by visiting the top-left corner.
visit(1, 1)
# Display the final resulting maze data structure:
printMaze(maze)The JavaScript code for this is as follows:
JavaScript
// Carve out the paths in the maze data structure:
let hasVisited = [[1, 1]]; // Start by visiting the top-left corner.
visit(1, 1);
// Display the final resulting maze data structure:
printMaze(maze);After setting up hasVisited to include the x, y coordinates of 1, 1 (the top-left corner of the maze), we call visit() with these coordinates. This function call will result in all the recursive function calls that generate the hallways of the maze. By the time this function call returns, hasVisited will contain every x, y coordinate of the maze, and maze will contain the completely generated maze.
As you just learned, we can use recursion to not only solve mazes (by traversing them as tree data structures) but also generate them using the recursive backtracker algorithm. The algorithm “carves out” hallways in the maze, backtracking to earlier points when it encounters a dead end. Once the algorithm is forced to backtrack to the starting point, the maze is completely generated.
We can represent a simply connected maze with no loops as a DAG—that is, a tree data structure. The recursive backtracker algorithm makes use of the idea that recursive algorithms are well suited to problems involving tree-like data structures and backtracking.
Wikipedia has an entry on maze generation in general, with a section on the recursive backtracker algorithm, at https://en.wikipedia.org/wiki/Maze_generation_algorithm#Recursive_backtracker. I’ve created a browser-based animation of the recursive backtracker algorithm that shows the “carving” of hallways in action at https://scratch.mit.edu/projects/17358777.
If maze generation interests you, you should read Mazes for Programmers: Code Your Own Twisty Little Passages by Jamis Buck (Pragmatic Bookshelf, 2015).