Check out other books by Al Sweigart, free online or available for purchase:




...and other books as well! Or register for the online video course. You can also donate to support the author directly.





A sliding-tile puzzle, or 15-puzzle, is a small puzzle game implemented as a set of 15 numbered sliding tiles on a 4 × 4 board. One tile is missing, allowing adjacent tiles to slide into the empty space on the board. The player’s goal is to move the tiles into numeric order, as in Figure 12-1. Some versions of this game have fragments of a picture on the tiles that create a whole image when the puzzle is complete.
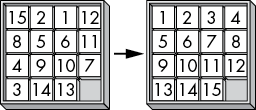
Figure 12-1: Solving a numeric sliding-tile puzzle from its scrambled state (left) to its solved, ordered state (right)
Incidentally, mathematicians have proven that even the hardest 15-puzzle can be solved in 80 moves.
The algorithm that solves 15-puzzles is similar to the maze-solving algorithm. Each state of the board (that is, one arrangement of tiles) can be thought of as a maze intersection with four hallways to go down. In the case of 15-puzzles, sliding a tile in one of the four directions is like picking a hallway to follow to the next intersection.
Just as you can turn a maze into a DAG, you can convert a 15-puzzle into a tree graph, as in Figure 12-2. The board states are nodes with up to four edges (representing a direction to slide a tile) to other nodes (representing the resultant state). The root node is the starting state of the 15-puzzle. The solved-state node is the one in which the tiles are ordered correctly. The path from the root node to the solved state details the slides needed to solve the puzzle.
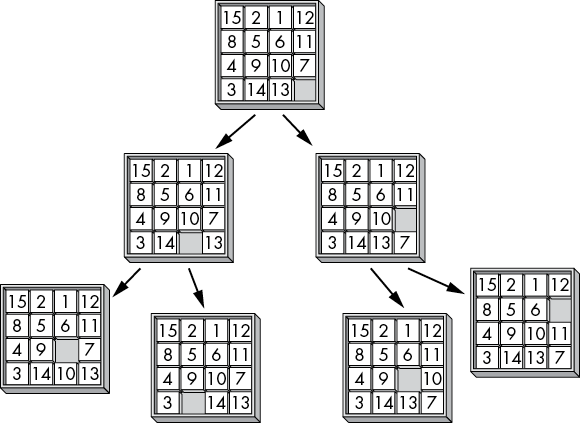
Figure 12-2: The task of solving a 15-puzzle can be represented as a graph with tile states as nodes and slides as edges.
Clever algorithms are available for solving 15-puzzles, but we could also just recursively explore the entire tree graph until we find a path from the root node to the solution node. This puzzle’s tree can be searched with a depth-first search (DFS) algorithm. However, unlike a simply connected maze, the 15-puzzle’s tree graph is not a DAG. Rather, the graph’s nodes are undirected, because you can traverse both directions of an edge by undoing the previous slide you made.
Figure 12-3 shows an example of the undirected edges between two nodes. Because it is possible to go back and forth between these two nodes forever, our 15-puzzle algorithm could encounter a stack overflow before it finds a solution.
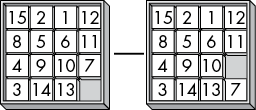
Figure 12-3: The 15-puzzle has undirected edges (drawn without an arrowhead) between its nodes because slides can be undone by performing the opposite slide.
To optimize our algorithm, we’ll avoid slides that undo the previous slide. However, this optimization alone won’t save the algorithm from a stack overflow. While it makes the edges in the tree graph directed, it doesn’t turn the puzzle-solver algorithm into a DAG, because it has cycles, or loops, from lower nodes to higher ones. These loops happen if you slide the tiles in a circular pattern, as in Figure 12-4.
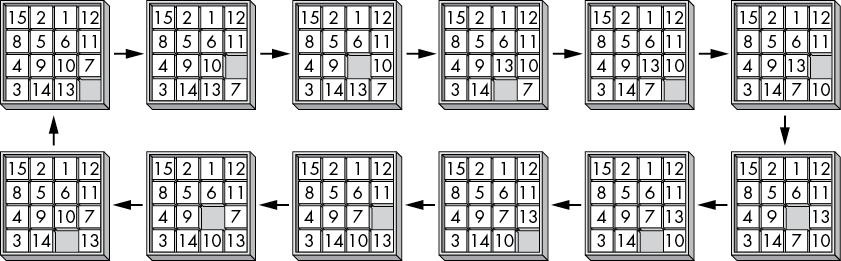
Figure 12-4: An example of a loop in the 15-puzzle’s graph
Cycles in the graph mean that the later nodes at the bottom could loop back to a node at the top. Our solving algorithm could get “stuck” following this loop and never explore the branch that has the actual solution. In practice, this infinite loop would result in a stack overflow.
We can still use recursion to solve a 15-puzzle. We just need to add our own base case for the maximum number of moves in order to avoid causing a stack overflow. Then, when the maximum number of slide moves is reached, the algorithm will begin backtracking to earlier nodes. If the 15-puzzle solver project can’t find a solution in every possible combination of 10 slides, it will try again using a maximum of 11 slides. If the puzzle can’t be solved in 11 moves, the project tries 12 moves, and so on. This prevents the algorithm from getting stuck exploring the moves of an infinite loop instead of exploring possible solutions of fewer moves.
Let’s begin by taking a look at the complete source code for the sliding-tile puzzle solver program. The rest of this chapter explains each section of code individually.
Copy the Python version of the code to a file named slidingTileSolver.py:
Python
import random, time
DIFFICULTY = 40 # How many random slides a puzzle starts with.
SIZE = 4 # The board is SIZE x SIZE spaces.
random.seed(1) # Select which puzzle to solve.
BLANK = 0
UP = 'up'
DOWN = 'down'
LEFT = 'left'
RIGHT = 'right'
def displayBoard(board):
"""Display the tiles stored in `board` on the screen."""
for y in range(SIZE): # Iterate over each row.
for x in range(SIZE): # Iterate over each column.
if board[y * SIZE + x] == BLANK:
print('__ ', end='') # Display blank tile.
else:
print(str(board[y * SIZE + x]).rjust(2) + ' ', end='')
print() # Print a newline at the end of the row.
def getNewBoard():
"""Return a list that represents a new tile puzzle."""
board = []
for i in range(1, SIZE * SIZE):
board.append(i)
board.append(BLANK)
return board
def findBlankSpace(board):
"""Return an [x, y] list of the blank space's location."""
for x in range(SIZE):
for y in range(SIZE):
if board[y * SIZE + x] == BLANK:
return [x, y]
def makeMove(board, move):
"""Modify `board` in place to carry out the slide in `move`."""
bx, by = findBlankSpace(board)
blankIndex = by * SIZE + bx
if move == UP:
tileIndex = (by + 1) * SIZE + bx
elif move == LEFT:
tileIndex = by * SIZE + (bx + 1)
elif move == DOWN:
tileIndex = (by - 1) * SIZE + bx
elif move == RIGHT:
tileIndex = by * SIZE + (bx - 1)
# Swap the tiles at blankIndex and tileIndex:
board[blankIndex], board[tileIndex] = board[tileIndex], board[blankIndex]
def undoMove(board, move):
"""Do the opposite move of `move` to undo it on `board`."""
if move == UP:
makeMove(board, DOWN)
elif move == DOWN:
makeMove(board, UP)
elif move == LEFT:
makeMove(board, RIGHT)
elif move == RIGHT:
makeMove(board, LEFT)
def getValidMoves(board, prevMove=None):
"""Returns a list of the valid moves to make on this board. If
prevMove is provided, do not include the move that would undo it."""
blankx, blanky = findBlankSpace(board)
validMoves = []
if blanky != SIZE - 1 and prevMove != DOWN:
# Blank space is not on the bottom row.
validMoves.append(UP)
if blankx != SIZE - 1 and prevMove != RIGHT:
# Blank space is not on the right column.
validMoves.append(LEFT)
if blanky != 0 and prevMove != UP:
# Blank space is not on the top row.
validMoves.append(DOWN)
if blankx != 0 and prevMove != LEFT:
# Blank space is not on the left column.
validMoves.append(RIGHT)
return validMoves
def getNewPuzzle():
"""Get a new puzzle by making random slides from the solved state."""
board = getNewBoard()
for i in range(DIFFICULTY):
validMoves = getValidMoves(board)
makeMove(board, random.choice(validMoves))
return board
def solve(board, maxMoves):
"""Attempt to solve the puzzle in `board` in at most `maxMoves`
moves. Returns True if solved, otherwise False."""
print('Attempting to solve in at most', maxMoves, 'moves...')
solutionMoves = [] # A list of UP, DOWN, LEFT, RIGHT values.
solved = attemptMove(board, solutionMoves, maxMoves, None)
if solved:
displayBoard(board)
for move in solutionMoves:
print('Move', move)
makeMove(board, move)
print() # Print a newline.
displayBoard(board)
print() # Print a newline.
print('Solved in', len(solutionMoves), 'moves:')
print(', '.join(solutionMoves))
return True # Puzzle was solved.
else:
return False # Unable to solve in maxMoves moves.
def attemptMove(board, movesMade, movesRemaining, prevMove):
"""A recursive function that attempts all possible moves on `board`
until it finds a solution or reaches the `maxMoves` limit.
Returns True if a solution was found, in which case `movesMade`
contains the series of moves to solve the puzzle. Returns False
if `movesRemaining` is less than 0."""
if movesRemaining < 0:
# BASE CASE - Ran out of moves.
return False
if board == SOLVED_BOARD:
# BASE CASE - Solved the puzzle.
return True
# RECURSIVE CASE - Attempt each of the valid moves:
for move in getValidMoves(board, prevMove):
# Make the move:
makeMove(board, move)
movesMade.append(move)
if attemptMove(board, movesMade, movesRemaining - 1, move):
# If the puzzle is solved, return True:
undoMove(board, move) # Reset to the original puzzle.
return True
# Undo the move to set up for the next move:
undoMove(board, move)
movesMade.pop() # Remove the last move since it was undone.
return False # BASE CASE - Unable to find a solution.
# Start the program:
SOLVED_BOARD = getNewBoard()
puzzleBoard = getNewPuzzle()
displayBoard(puzzleBoard)
startTime = time.time()
maxMoves = 10
while True:
if solve(puzzleBoard, maxMoves):
break # Break out of the loop when a solution is found.
maxMoves += 1
print('Run in', round(time.time() - startTime, 3), 'seconds.')Copy the JavaScript version of the code to a file named slidingTileSolver.html:
<script type="text/javascript">
const DIFFICULTY = 40; // How many random slides a puzzle starts with.
const SIZE = 4; // The board is SIZE x SIZE spaces.
const BLANK = 0;
const UP = "up";
const DOWN = "down";
const LEFT = "left";
const RIGHT = "right";
function displayBoard(board) {
// Display the tiles stored in `board` on the screen.
document.write("<pre>");
for (let y = 0; y < SIZE; y++) { // Iterate over each row.
for (let x = 0; x < SIZE; x++) { // Iterate over each column.
if (board[y * SIZE + x] == BLANK) {
document.write('__ '); // Display blank tile.
} else {
document.write(board[y * SIZE + x].toString().padStart(2) + " ");
}
}
document.write("<br />"); // Print a newline at the end of the row.
}
document.write("</pre>");
}
function getNewBoard() {
// Return a list that represents a new tile puzzle.
let board = [];
for (let i = 1; i < SIZE * SIZE; i++) {
board.push(i);
}
board.push(BLANK);
return board;
}
function findBlankSpace(board) {
// Return an [x, y] array of the blank space's location.
for (let x = 0; x < SIZE; x++) {
for (let y = 0; y < SIZE; y++) {
if (board[y * SIZE + x] === BLANK) {
return [x, y];
}
}
}
}
function makeMove(board, move) {
// Modify `board` in place to carry out the slide in `move`.
let bx, by;
[bx, by] = findBlankSpace(board);
let blankIndex = by * SIZE + bx;
let tileIndex;
if (move === UP) {
tileIndex = (by + 1) * SIZE + bx;
} else if (move === LEFT) {
tileIndex = by * SIZE + (bx + 1);
} else if (move === DOWN) {
tileIndex = (by - 1) * SIZE + bx;
} else if (move === RIGHT) {
tileIndex = by * SIZE + (bx - 1);
}
// Swap the tiles at blankIndex and tileIndex:
[board[blankIndex], board[tileIndex]] = [board[tileIndex], board[blankIndex]];
}
function undoMove(board, move) {
// Do the opposite move of `move` to undo it on `board`.
if (move === UP) {
makeMove(board, DOWN);
} else if (move === DOWN) {
makeMove(board, UP);
} else if (move === LEFT) {
makeMove(board, RIGHT);
} else if (move === RIGHT) {
makeMove(board, LEFT);
}
}
function getValidMoves(board, prevMove) {
// Returns a list of the valid moves to make on this board. If
// prevMove is provided, do not include the move that would undo it.
let blankx, blanky;
[blankx, blanky] = findBlankSpace(board);
let validMoves = [];
if (blanky != SIZE - 1 && prevMove != DOWN) {
// Blank space is not on the bottom row.
validMoves.push(UP);
}
if (blankx != SIZE - 1 && prevMove != RIGHT) {
// Blank space is not on the right column.
validMoves.push(LEFT);
}
if (blanky != 0 && prevMove != UP) {
// Blank space is not on the top row.
validMoves.push(DOWN);
}
if (blankx != 0 && prevMove != LEFT) {
// Blank space is not on the left column.
validMoves.push(RIGHT);
}
return validMoves;
}
function getNewPuzzle() {
// Get a new puzzle by making random slides from the solved state.
let board = getNewBoard();
for (let i = 0; i < DIFFICULTY; i++) {
let validMoves = getValidMoves(board);
makeMove(board, validMoves[Math.floor(Math.random() * validMoves.length)]);
}
return board;
}
function solve(board, maxMoves) {
// Attempt to solve the puzzle in `board` in at most `maxMoves`
// moves. Returns true if solved, otherwise false.
document.write("Attempting to solve in at most " + maxMoves + " moves...<br />");
let solutionMoves = []; // A list of UP, DOWN, LEFT, RIGHT values.
let solved = attemptMove(board, solutionMoves, maxMoves, null);
if (solved) {
displayBoard(board);
for (let move of solutionMoves) {
document.write("Move " + move + "<br />");
makeMove(board, move);
document.write("<br />"); // Print a newline.
displayBoard(board);
document.write("<br />"); // Print a newline.
}
document.write("Solved in " + solutionMoves.length + " moves:<br />");
document.write(solutionMoves.join(", ") + "<br />");
return true; // Puzzle was solved.
} else {
return false; // Unable to solve in maxMoves moves.
}
}
function attemptMove(board, movesMade, movesRemaining, prevMove) {
// A recursive function that attempts all possible moves on `board`
// until it finds a solution or reaches the `maxMoves` limit.
// Returns true if a solution was found, in which case `movesMade`
// contains the series of moves to solve the puzzle. Returns false
// if `movesRemaining` is less than 0.
if (movesRemaining < 0) {
// BASE CASE - Ran out of moves.
return false;
}
if (JSON.stringify(board) == SOLVED_BOARD) {
// BASE CASE - Solved the puzzle.
return true;
}
// RECURSIVE CASE - Attempt each of the valid moves:
for (let move of getValidMoves(board, prevMove)) {
// Make the move:
makeMove(board, move);
movesMade.push(move);
if (attemptMove(board, movesMade, movesRemaining - 1, move)) {
// If the puzzle is solved, return true:
undoMove(board, move); // Reset to the original puzzle.
return true;
}
// Undo the move to set up for the next move:
undoMove(board, move);
movesMade.pop(); // Remove the last move since it was undone.
}
return false; // BASE CASE - Unable to find a solution.
}
// Start the program:
const SOLVED_BOARD = JSON.stringify(getNewBoard());
let puzzleBoard = getNewPuzzle();
displayBoard(puzzleBoard);
let startTime = Date.now();
let maxMoves = 10;
while (true) {
if (solve(puzzleBoard, maxMoves)) {
break; // Break out of the loop when a solution is found.
}
maxMoves += 1;
}
document.write("Run in " + Math.round((Date.now() - startTime) / 100) / 10 + " seconds.<br />");
</script>The program’s output looks like the following:
7 1 3 4
2 5 10 8
__ 6 9 11
13 14 15 12
Attempting to solve in at most 10 moves...
Attempting to solve in at most 11 moves...
Attempting to solve in at most 12 moves...
--snip--
1 2 3 4
5 6 7 8
9 10 11 __
13 14 15 12
Move up
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 __
Solved in 18 moves:
left, down, right, down, left, up, right, up, left, left, down,
right, right, up, left, left, left, up
Run in 39.519 seconds.Note that when JavaScript runs in a browser, the code must complete before it displays any output. Until then, it may appear to have frozen, and your browser might ask if you’d like to prematurely stop it. You can ignore this warning and let the program keep working until it has solved the puzzle.
The program’s recursive attemptMove() function solves sliding-tile puzzles by trying every possible combination of slides. The function is given a move to try. If this solves the puzzle, the function returns a Boolean True value. Otherwise, it calls attemptMove() with all the other possible moves it can make and returns a Boolean False value if none of them find a solution before exceeding the maximum number of moves. We’ll explore this function in more detail later.
The data structure we use to represent a sliding-tile board is a list (in Python) or array (in JavaScript) of integers, with 0 representing the blank space. In our program, this data structure is often stored in a variable named board. The values at board[y * SIZE + x] match the tile at the x, y coordinates on the board, as depicted in Figure 12-5. For example, if the SIZE constant is 4, the value at the x, y coordinates 3, 1 can be found at board[1 * 4 + 3].
This small calculation enables us to use a 1D array or list to store the values of a 2D tile board. This programming technique is useful not just in our project but for any 2D data structure that must be stored in an array or list, such as a 2D image stored as a stream of bytes.
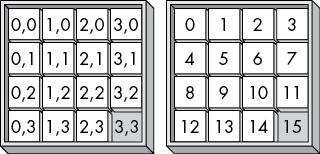
Figure 12-5: The x, y coordinates for each space on the board (left) and the corresponding data structure index (right)
Let’s look at some example data structures. The board with mixed-up tiles shown previously on the left side of Figure 12-1 would be represented by the following:
[15, 2, 1, 12, 8, 5, 6, 11, 4, 9, 10, 7, 3, 14, 13, 0] The solved, ordered puzzle on the right side of Figure 12-1 would be represented by this:
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 0]All the functions in our program will expect board data structures that follow this format.
Unfortunately, the 4 × 4 version of the sliding-tile puzzle has so many possible moves that it would take a normal laptop weeks to solve. You can change the SIZE constant from 4 to 3 to solve a simpler 3 × 3 version of the puzzle. The finished, ordered 3 × 3 puzzle’s data structure would look like this:
[1, 2, 3, 4, 5, 6, 7, 8, 0].At the beginning of the source code, the program uses a few constants to make the code more readable. The Python code is as follows:
Python
import random, time
DIFFICULTY = 40 # How many random slides a puzzle starts with.
SIZE = 4 # The board is SIZE x SIZE spaces.
random.seed(1) # Select which puzzle to solve.
BLANK = 0
UP = 'up'
DOWN = 'down'
LEFT = 'left'
RIGHT = 'right'The JavaScript code is as follows:
JavaScript
<script type="text/javascript">
const DIFFICULTY = 40; // How many random slides a puzzle starts with.
const SIZE = 4; // The board is SIZE x SIZE spaces.
const BLANK = 0;
const UP = "up";
const DOWN = "down";
const LEFT = "left";
const RIGHT = "right";To have reproducible random numbers, the Python program sets the random number seed to 1. The same seed value will always reproduce the same random puzzle, which is useful for debugging. You can change the seed value to any other integer to create different puzzles. JavaScript has no way to set its random seed value, and slidingtilesolver.html doesn’t have an equivalent feature.
The SIZE constant sets the size of the square board. You can change this size to anything, but 4 × 4 boards are standard, while 3 × 3 boards are useful for testing, because the program is quick to solve them. The BLANK constant is used in the puzzle data structure to represent the blank space and must be kept at 0. The UP, DOWN, LEFT, and RIGHT constants are used to make the code readable, similar to the NORTH, SOUTH, WEST, and EAST constants in the maze-generator project in Chapter 11.
The sliding-tile board’s data structure is just a list or array of integers. What makes it representative of an actual puzzle board is the way it’s used by the functions in the program. The displayBoard(), getNewBoard(), findBlankSpace(), and other functions in this program all deal with this data structure.
The first function, displayBoard(), prints the board data structure on the screen. The Python code for the displayBoard() function is as follows:
Python
def displayBoard(board):
"""Display the tiles stored in `board` on the screen."""
for y in range(SIZE): # Iterate over each row.
for x in range(SIZE): # Iterate over each column.
if board[y * SIZE + x] == BLANK:
print('__ ', end='') # Display blank tile.
else:
print(str(board[y * SIZE + x]).rjust(2) + ' ', end='')
print() # Print a newline at the end of the row.The JavaScript code for the displayBoard() function is as follows:
function displayBoard(board) {
// Display the tiles stored in `board` on the screen.
document.write("<pre>");
for (let y = 0; y < SIZE; y++) { // Iterate over each row.
for (let x = 0; x < SIZE; x++) { // Iterate over each column.
if (board[y * SIZE + x] == BLANK) {
document.write('__ '); // Display blank tile.
} else {
document.write(board[y * SIZE + x].toString().padStart(2) + " ");
}
}
document.write("<br />");
}
document.write("</pre>");
}The pair of nested for loops iterate over every row and column on the board. The first for loop loops over the y-coordinates, and the second for loop loops over the x-coordinates. This is because the program needs to print all the columns of a single row before printing a newline character to move on to the next row.
The if statement checks whether the tile at the current x, y coordinates is the blank tile. If it is, the program prints two underscores with a trailing space. Otherwise, the code in the else block prints the tile number with a trailing space. The trailing space is what separates the tile numbers from one another on the screen. If the tile number is a single digit, the rjust() or padStart() method will insert an extra space so that the tile number is aligned with the two-digit numbers on the screen.
For example, say the scrambled puzzle on the left side of Figure 12-1 is represented by this data structure:
[15, 2, 1, 12, 8, 5, 6, 11, 4, 9, 10, 7, 3, 14, 13, 0]
When the data structure is passed to displayBoard(), it prints the following text:
15 2 1 12
8 5 6 11
4 9 10 7
3 14 13 __Next, the getNewBoard() function returns a new board data structure with the tiles in their ordered, solved places. The Python code for the getNewBoard() function is as follows:
Python
def getNewBoard():
"""Return a list that represents a new tile puzzle."""
board = []
for i in range(1, SIZE * SIZE):
board.append(i)
board.append(BLANK)
return boardThe JavaScript code for the getNewBoard() function is as follows:
JavaScript
function getNewBoard() {
// Return a list that represents a new tile puzzle.
let board = [];
for (let i = 1; i < SIZE * SIZE; i++) {
board.push(i);
}
board.push(BLANK);
return board;
}The getNewBoard() function returns a board data structure appropriate to the integer in the SIZE constant (either 3 × 3 or 4 × 4). The for loop generates this list or array with the integers from 1 up to, but not including, SIZE squared, with a 0 (the value stored in the BLANK constant) at the end to represent the blank space in the lower-right corner.
Our program uses the findBlankSpace() function to find the x, y coordinates of the blank space on the board. The Python code is as follows:
Python
def findBlankSpace(board):
"""Return an [x, y] list of the blank space's location."""
for x in range(SIZE):
for y in range(SIZE):
if board[y * SIZE + x] == BLANK:
return [x, y]The JavaScript code is as follows:
JavaScript
function findBlankSpace(board) {
// Return an [x, y] array of the blank space's location.
for (let x = 0; x < SIZE; x++) {
for (let y = 0; y < SIZE; y++) {
if (board[y * SIZE + x] === BLANK) {
return [x, y];
}
}
}
}Like the displayBoard() function, the findBlankSpace() function has a pair of nested for loops. These for loops will loop over every position in the board data structure. When the board[y * SIZE + x] code finds the blank space, it returns the x- and y-coordinates as two integers in a Python list or JavaScript array.
Next, the makeMove() function accepts two arguments: a board data structure and an UP, DOWN, LEFT, or RIGHT direction to slide a tile on that board. This code is fairly repetitive, so the short variable names bx and by are used to represent the x- and y-coordinates of the blank space.
To make a move, the board data structure swaps the value of the moved tile with the 0 of the blank tile. The Python code for the makeMove() function is as follows:
Python
def makeMove(board, move):
"""Modify `board` in place to carry out the slide in `move`."""
bx, by = findBlankSpace(board)
blankIndex = by * SIZE + bx
if move == UP:
tileIndex = (by + 1) * SIZE + bx
elif move == LEFT:
tileIndex = by * SIZE + (bx + 1)
elif move == DOWN:
tileIndex = (by - 1) * SIZE + bx
elif move == RIGHT:
tileIndex = by * SIZE + (bx - 1)
# Swap the tiles at blankIndex and tileIndex:
board[blankIndex], board[tileIndex] = board[tileIndex], board[blankIndex]The JavaScript code for the makeMove() function is as follows:
function makeMove(board, move) {
// Modify `board` in place to carry out the slide in `move`.
let bx, by;
[bx, by] = findBlankSpace(board);
let blankIndex = by * SIZE + bx;
let tileIndex;
if (move === UP) {
tileIndex = (by + 1) * SIZE + bx;
} else if (move === LEFT) {
tileIndex = by * SIZE + (bx + 1);
} else if (move === DOWN) {
tileIndex = (by - 1) * SIZE + bx;
} else if (move === RIGHT) {
tileIndex = by * SIZE + (bx - 1);
}
// Swap the tiles at blankIndex and tileIndex:
[board[blankIndex], board[tileIndex]] = [board[tileIndex], board[blankIndex]];
}The if statements determine the index of the tile to move based on the move parameter. The function then “slides” a tile by swapping the BLANK value at board[blankindex] with the numbered tile at board[tileIndex]. The makeMove() function doesn’t return anything. Instead, it modifies the board data structure in place.
Python has the a, b = b, a syntax to swap the value of two variables. For JavaScript, we need to envelop them in an array, such as [a, b] = [b, a] to perform the swap. We use this syntax at the end of the function to swap the values in board[blankIndex] and board[tileIndex] with each other.
Next, as part of the backtracking in the recursive algorithm, our program needs to undo moves. This is as simple as making a move in the opposite direction as the initial move. The Python code for the undoMove() function is as follows:
Python
def undoMove(board, move):
"""Do the opposite move of `move` to undo it on `board`."""
if move == UP:
makeMove(board, DOWN)
elif move == DOWN:
makeMove(board, UP)
elif move == LEFT:
makeMove(board, RIGHT)
elif move == RIGHT:
makeMove(board, LEFT)The JavaScript code for the undoMove() function is as follows:
JavaScript
function undoMove(board, move) {
// Do the opposite move of `move` to undo it on `board`.
if (move === UP) {
makeMove(board, DOWN);
} else if (move === DOWN) {
makeMove(board, UP);
} else if (move === LEFT) {
makeMove(board, RIGHT);
} else if (move === RIGHT) {
makeMove(board, LEFT);
}
}We’ve already programmed the swapping logic into the makeMove() function, so undoMove() can just call that function for the direction opposite of the move argument. This way, a hypothetical someMove move made on a hypothetical someBoard data structure by the makeMove(someBoard, someMove) function call can be undone by calling undoMove(someBoard, someMove).
To create a new, scrambled puzzle, we cannot simply put the tiles in random places, because some configurations of tiles produce invalid, unsolvable puzzles. Instead, we need to start from a solved puzzle and make many random moves. Solving the puzzle becomes a matter of figuring out which slides will undo these random slides to get back to the original, ordered configuration.
But it’s not always possible to make moves in each of the four directions. For example, if the blank space is in the bottom-right corner, as in Figure 12-6, tiles can slide only down or right because no tiles can slide left or up. Furthermore, if sliding the 7 tile in Figure 12-6 up was the previous move, then sliding it down is removed as a valid move because it would undo the previous move.
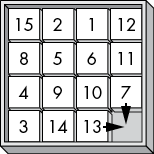
Figure 12-6: If the blank space is in the bottom-right corner, down and right are the only valid slide directions.
To help us, we need a getValidMoves() function that can tell us which slide directions are possible on a given board data structure:
Python
def getValidMoves(board, prevMove=None):
"""Returns a list of the valid moves to make on this board. If
prevMove is provided, do not include the move that would undo it."""
blankx, blanky = findBlankSpace(board)
validMoves = []
if blanky != SIZE - 1 and prevMove != DOWN:
# Blank space is not on the bottom row.
validMoves.append(UP)
if blankx != SIZE - 1 and prevMove != RIGHT:
# Blank space is not on the right column.
validMoves.append(LEFT)
if blanky != 0 and prevMove != UP:
# Blank space is not on the top row.
validMoves.append(DOWN)
if blankx != 0 and prevMove != LEFT:
# Blank space is not on the left column.
validMoves.append(RIGHT)
return validMovesThe JavaScript code for this function is as follows:
JavaScript
function getValidMoves(board, prevMove) {
// Returns a list of the valid moves to make on this board. If
// prevMove is provided, do not include the move that would undo it.
let blankx, blanky;
[blankx, blanky] = findBlankSpace(board);
let validMoves = [];
if (blanky != SIZE - 1 && prevMove != DOWN) {
// Blank space is not on the bottom row.
validMoves.push(UP);
}
if (blankx != SIZE - 1 && prevMove != RIGHT) {
// Blank space is not on the right column.
validMoves.push(LEFT);
}
if (blanky != 0 && prevMove != UP) {
// Blank space is not on the top row.
validMoves.push(DOWN);
}
if (blankx != 0 && prevMove != LEFT) {
// Blank space is not on the left column.
validMoves.push(RIGHT);
}
return validMoves;
}The first thing the getValidMoves() function does is call findBlankSpace() and store the x, y coordinates of the blank space in the variables blankx and blanky. Next, the function sets up the validMoves variable with an empty Python list or empty JavaScript array to hold all the valid directions for a slide.
Looking back at Figure 12-5, a y-coordinate of 0 represents the top edge of the board. If blanky, the blank space’s y-coordinate, is not 0, then we know the blank space is not on the top edge. If the previous move was also not DOWN, then up is a valid move, and the code adds UP to validMoves.
Similarly, the left edge has an x-coordinate of 0, the bottom edge has a y-coordinate of SIZE - 1, and the right edge has an x-coordinate of SIZE - 1. Using the expression SIZE - 1 ensures that this code works no matter whether the board is 3 × 3, 4 × 4, or any other size. The getValidMoves() function does these checks for all four directions and then returns validMoves.
Next, the getNewPuzzle() function returns the data structure of a scrambled board for the program to solve. Tiles can’t simply be randomly placed on the board, because some configurations of tiles produce puzzles that are impossible to solve. To avoid this, the getNewPuzzle() function starts with an ordered, solved board and then applies a large number of random slides to it. Solving this puzzle is, in effect, figuring out the moves that undo these slides. The Python code for the getNewPuzzle() function is as follows:
Python
def getNewPuzzle():
"""Get a new puzzle by making random slides from the solved state."""
board = getNewBoard()
for i in range(DIFFICULTY):
validMoves = getValidMoves(board)
makeMove(board, random.choice(validMoves))
return boardThe JavaScript code is as follows:
function getNewPuzzle() {
// Get a new puzzle by making random slides from the solved state.
let board = getNewBoard();
for (let i = 0; i < DIFFICULTY; i++) {
let validMoves = getValidMoves(board);
makeMove(board, validMoves[Math.floor(Math.random() * validMoves.length)]);
}
return board;
}The call to getNewBoard() obtains a board data structure in the ordered, solved state. The for loop calls getValidMoves() to obtain a list of valid moves, given the current state of the board, and then calls makeMove() with a randomly selected move from the list. The random.choice() function in Python and the Math.floor() and Math.random() functions in JavaScript will handle the random selection from the validMoves list or array, no matter what combination of UP, DOWN, LEFT, and RIGHT values it contains.
The DIFFICULTY constant determines how many random slides from makeMove() the for loop applies. The higher the integer in DIFFICULTY, the more scrambled the puzzle becomes. Even though this results in some moves that undo earlier moves by pure chance, such as sliding left and then immediately sliding right, with enough slides the function produces a thoroughly scrambled board. For testing purposes, DIFFICULTY is set to 40, allowing the program to produce a solution in about a minute. For a more realistic 15-puzzle, you should change DIFFICULTY to 200.
After the board data structure in board is created and scrambled, the getNewPuzzle() function returns it.
Now that we have the functions for creating and manipulating the puzzle data structure, let’s create the functions that solve the puzzle by recursively sliding the tiles in each possible direction and checking whether this produces a finished, ordered board.
The attemptMove() function performs a single slide on a board data structure, then recursively calls itself once for each of the valid moves the board can make. Multiple base cases exist. If the board data structure is in a solved state, the function returns a Boolean True value; if the maximum number of moves has been reached, it returns a Boolean False value. Also, if a recursive call has returned True, then attemptMove() should return True, and if recursive calls for all the valid moves have returned False, then attemptMove() should return False.
The solve() function takes a board data structure and maximum number of moves the algorithm should attempt before backtracking. Then it performs the first call to attemptMove(). If this first call to attemptMove() returns True, the code in solve() displays the series of steps that solves the puzzle. If it returns False, the code in solve() tells the user no solution was found with this maximum number of moves.
The Python code for solve() begins as follows:
Python
def solve(board, maxMoves):
"""Attempt to solve the puzzle in `board` in at most `maxMoves`
moves. Returns True if solved, otherwise False."""
print('Attempting to solve in at most', maxMoves, 'moves...')
solutionMoves = [] # A list of UP, DOWN, LEFT, RIGHT values.
solved = attemptMove(board, solutionMoves, maxMoves, None)The JavaScript code for solve() begins as follows:
function solve(board, maxMoves) {
// Attempt to solve the puzzle in `board` in at most `maxMoves`
// moves. Returns true if solved, otherwise false.
document.write("Attempting to solve in at most " + maxMoves + " moves...<br />");
let solutionMoves = []; // A list of UP, DOWN, LEFT, RIGHT values.
let solved = attemptMove(board, solutionMoves, maxMoves, null);The solve() function has two parameters: board contains the data structure of the puzzle to solve, and maxMoves is the maximum number of moves the function should make to try to solve the puzzle. The solutionMoves list or array contains the sequence of UP, DOWN, LEFT, and RIGHT values that produce the solved state. The attemptMove() function modifies this list or array in place as it makes recursive calls. If the initial attemptMove() function finds a solution and returns True, solutionMoves contains the sequence of moves for the solution.
The solve() function then makes the initial call to attemptMove(), and stores the True or False it returns in the solved variable. The rest of the solve() function handles these two cases:
Python
if solved:
displayBoard(board)
for move in solutionMoves:
print('Move', move)
makeMove(board, move)
print() # Print a newline.
displayBoard(board)
print() # Print a newline.
print('Solved in', len(solutionMoves), 'moves:')
print(', '.join(solutionMoves))
return True # Puzzle was solved.
else:
return False # Unable to solve in maxMoves moves.The JavaScript code is as follows:
JavaScript
if (solved) {
displayBoard(board);
for (let move of solutionMoves) {
document.write("Move " + move + "<br />");
makeMove(board, move);
document.write("<br />"); // Print a newline.
displayBoard(board);
document.write("<br />"); // Print a newline.
}
document.write("Solved in " + solutionMoves.length + " moves:<br />");
document.write(solutionMoves.join(", ") + "<br />");
return true; // Puzzle was solved.
} else {
return false; // Unable to solve in maxMoves moves.
}
}If attemptMove() finds a solution, the program runs through all the moves gathered in the solutionMoves list or array and displays the board after each slide. This proves to the user that the moves collected by attemptMove() are the real solution to the puzzle. Finally, the solve() function itself returns True. If attemptMove() is unable to find a solution, the solve() function simply returns False.
Let’s take a look at attemptMove(), the core recursive function behind our tile-solving algorithm. Remember the tree graph that a sliding-tile puzzle produces; calling attemptMove() for a certain direction is like traveling down that edge of this graph to the next node. A recursive attemptMove() call moves further down the tree. When this recursive attemptMove() call returns, it backtracks to a previous node. When attemptMove() has backtracked all the way to the root node, the program execution has returned to the solve() function.
The Python code for attemptMove() begins as follows:
Python
def attemptMove(board, movesMade, movesRemaining, prevMove):
"""A recursive function that attempts all possible moves on `board`
until it finds a solution or reaches the `maxMoves` limit.
Returns True if a solution was found, in which case `movesMade`
contains the series of moves to solve the puzzle. Returns False
if `movesRemaining` is less than 0."""
if movesRemaining < 0:
# BASE CASE - Ran out of moves.
return False
if board == SOLVED_BOARD:
# BASE CASE - Solved the puzzle.
return TrueThe JavaScript code for attemptMove() begins as follows:
JavaScript
function attemptMove(board, movesMade, movesRemaining, prevMove) {
// A recursive function that attempts all possible moves on `board`
// until it finds a solution or reaches the `maxMoves` limit.
// Returns true if a solution was found, in which case `movesMade`
// contains the series of moves to solve the puzzle. Returns false
// if `movesRemaining` is less than 0.
if (movesRemaining < 0) {
// BASE CASE - Ran out of moves.
return false;
}
if (JSON.stringify(board) == SOLVED_BOARD) {
// BASE CASE - Solved the puzzle.
return true;
}The attemptMove() function has four parameters. The board parameter contains a tile puzzle board data structure to solve. The movesMade parameter contains a list or array that attemptMove() modifies in place, adding the UP, DOWN, LEFT, and RIGHT values that the recursive algorithm has made. If attemptMove() solves the puzzle, movesMade will contain the moves that led to the solution. This list or array is also what the solutionMoves variable in the solve() function refers to.
The solve() function uses its maxMoves variable as the movesRemaining parameter in the initial call to attemptMove(). Each recursive call passes maxMoves - 1 for the next value of maxMoves, causing it to decrease as more recursive calls are made. When it becomes less than 0, the attemptMove() function stops making additional recursive calls and returns False.
Finally, the prevMove parameter contains the UP, DOWN, LEFT, or RIGHT value that the previous call to attemptMove() made so that it doesn’t undo that move. For the initial call to attemptMove(), the solve() function passes Python’s None or JavaScript’s null value for this parameter, since no previous move exists.
The beginning of the attemptMove() code checks for two base cases, returning False if movesRemaining has become less than 0, and returning True if board is in the solved state. The SOLVED_BOARD constant contains a board in the solved state that we can compare to the data structure in board.
The next part of attemptMove() performs each of the valid moves it can do on this board. The Python code is as follows:
Python
# RECURSIVE CASE - Attempt each of the valid moves:
for move in getValidMoves(board, prevMove):
# Make the move:
makeMove(board, move)
movesMade.append(move)
if attemptMove(board, movesMade, movesRemaining - 1, move):
# If the puzzle is solved, return True:
undoMove(board, move) # Reset to the original puzzle.
return TrueThe JavaScript code is as follows:
JavaScript
// RECURSIVE CASE - Attempt each of the valid moves:
for (let move of getValidMoves(board, prevMove)) {
// Make the move:
makeMove(board, move);
movesMade.push(move);
if (attemptMove(board, movesMade, movesRemaining - 1, move)) {
// If the puzzle is solved, return True:
undoMove(board, move); // Reset to the original puzzle.
return true;
}The for loop sets the move variable to each of the directions returned by getValidMoves(). For each move, we call makeMove() to modify the board data structure with the move and to add the move to the list or array in movesMade.
Next, the code recursively calls attemptMove() to explore the range of all possible future moves within the depth set by movesRemaining. The board and movesMade variables are forwarded to this recursive call. The code sets the recursive call’s movesRemaining parameter to movesRemaining - 1 so that it decreases by one. It also sets the prevMode parameter to move so that it doesn’t immediately undo the move just made.
If the recursive call returns True, a solution exists and is recorded in the movesMade list or array. We call the undoMove() function so that board will contain the original puzzle after the execution returns to solve() and then return True to indicate a solution has been found.
The Python code for attemptMove() continues as follows:
Python
# Undo the move to set up for the next move:
undoMove(board, move)
movesMade.pop() # Remove the last move since it was undone.
return False # BASE CASE - Unable to find a solution.The JavaScript code is as follows:
JavaScript
// Undo the move to set up for the next move:
undoMove(board, move);
movesMade.pop(); // Remove the last move since it was undone.
}
return false; // BASE CASE - Unable to find a solution.
}If attemptMove() returns False, no solution is found. In that case, we call undoMove() and remove the latest move from the movesMade list or array.
All of this is done for each of the valid directions. If none of the calls to attemptMove() for these directions finds a solution before reaching the maximum number of moves, the attemptMove() function returns False.
The solve() function is useful for kicking off the initial call to attemptMove(), but the program still needs to do some setup. The Python code for this is as follows:
Python
# Start the program:
SOLVED_BOARD = getNewBoard()
puzzleBoard = getNewPuzzle()
displayBoard(puzzleBoard)
startTime = time.time()The JavaScript code for this setup is as follows:
JavaScript
// Start the program:
const SOLVED_BOARD = JSON.stringify(getNewBoard());
let puzzleBoard = getNewPuzzle();
displayBoard(puzzleBoard);
let startTime = Date.now();First, the SOLVED_BOARD constant is set to an ordered, solved board as returned by getNewBoard(). This constant isn’t set at the top of the source code because the getNewBoard() function needs to be defined before it can be called.
Next, a random puzzle is returned from getNewPuzzle() and stored in the puzzleBoard variable. This variable contains the puzzle board data structure that will be solved. If you want to solve a specific 15-puzzle instead of a random one, you can replace the call to getNewPuzzle() with a list or array containing the puzzle you do want to solve.
The board in puzzleBoard is displayed to the user, and the current time is stored in startTime so that the program can calculate the runtime of the algorithm. The Python code continues as follows:
Python
maxMoves = 10
while True:
if solve(puzzleBoard, maxMoves):
break # Break out of the loop when a solution is found.
maxMoves += 1
print('Run in', round(time.time() - startTime, 3), 'seconds.')The JavaScript code is as follows:
let maxMoves = 10;
while (true) {
if (solve(puzzleBoard, maxMoves)) {
break; // Break out of the loop when a solution is found.
}
maxMoves += 1;
}
document.write("Run in " + Math.round((Date.now() - startTime) / 100) / 10 + " seconds.<br />");
</script>The program begins trying to solve the puzzle in puzzleBoard in a maximum of 10 moves. The infinite while loop calls solve(). If a solution is found, solve() prints the solution on the screen and returns True. In that case, the code here can break out of the infinite while loop and print the total runtime of the algorithm.
Otherwise, if solve() returns False, maxMoves is incremented by 1 and the loop calls solve() again. This lets the program try progressively longer combinations of moves to solve the puzzle. This pattern continues until solve() finally returns True.
A 15-puzzle is a good example of adapting the principles of recursion to a real-world problem. Recursion can perform a depth-first search on the tree graph of states that a 15-puzzle produces to find the path to a solution state. However, a purely recursive algorithm won’t work, which was why we had to make certain adjustments.
The problem arises because a 15-puzzle has a massive number of possible states and doesn’t form a DAG. The edges in this graph are undirected, and the graph contains loops, or cycles. Our solving algorithm needs to ensure that it doesn’t make moves that immediately undo the previous move, so that it traverses the graph in one direction. It also needs to have a maximum number of moves the algorithm is willing to make before it begins to backtrack; otherwise, the loops guarantee that the algorithm will eventually recurse too much and cause a stack overflow.
Recursion isn’t necessarily the best approach for solving sliding-tile puzzles. All but the easiest puzzles simply have too many combinations for a typical laptop to solve within a reasonable amount of time. However, I like the 15-puzzle as an exercise in recursion because it connects the theoretical ideas of DAGs and DFS into a real-world problem. While 15-puzzles were invented over a century ago, the advent of computers provides a rich tool for exploring techniques to solve these amusing toys.
The Wikipedia entry for 15-puzzles at https://en.wikipedia.org/wiki/15_puzzle details their history and mathematical background.
You can find the Python source code for a playable version of the sliding-tile puzzle game in my book The Big Book of Small Python Projects (No Starch Press, 2021) and online at https://inventwithpython.com/bigbookpython/project68.html.