Check out other books by Al Sweigart, free online or available for purchase:




...and other books as well! Or register for the online video course. You can also donate to support the author directly.





Chapter 9 introduced you to programs that draw many well-known fractals with the turtle Python module, but you can also make your own fractal art with the project in this chapter. The Fractal Art Maker program uses Python’s turtle module to turn simple shapes into complex designs with minimal additional code.
The project in this chapter comes with nine example fractals, although you can also write new functions to create fractals of your design. Modify the example fractals to produce radically different artwork or write code from scratch to implement your own creative vision.
You can direct your computer to create an unlimited number of fractals. Figure 13-1 shows the nine fractals that come with the Fractal Art Maker program that we’ll use in this chapter. These are produced from functions that draw a simple square or equilateral triangle as the base shape, then introduce slight differences in their recursive configuration to produce completely different images.

Figure 13-1: The nine example fractals that come with the Fractal Art Maker program
You can produce all of these fractals by setting the DRAW_FRACTAL constant at the top of the program to an integer from 1 to 9 and then running the Fractal Art Maker program. You can also set DRAW_FRACTAL to 10 or 11 to draw the basic square and triangle shapes, respectively, that compose these fractals, as shown in Figure 13-2.
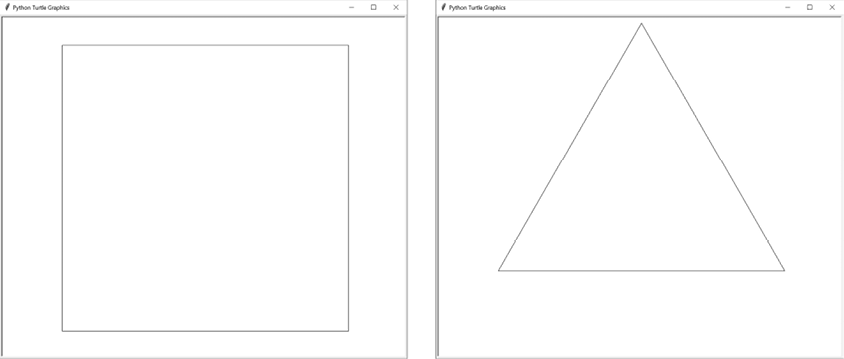
Figure 13-2: The results of calling drawFilledSquare() (left) and drawTriangleOutline() (right) on their own
These shapes are fairly simple: a square filled with either white or gray, and a simple outline of a triangle. The drawFractal() function uses these basic shapes to create amazing fractals.
The Fractal Art Maker’s algorithm has two major components: a shape-drawing function and the recursive drawFractal() function.
The shape-drawing function draws a basic shape. The Fractal Art Maker program comes with the two shape-drawing functions shown previously in Figure 13-2, drawFilledSquare() and drawTriangleOutline(), but you can also create your own. We pass a shape-drawing function to the drawFractal() function as an argument, just as we passed the match functions to the file finder’s walk() function in Chapter 10.
The drawFractal() function also has a parameter indicating changes to the size, position, and angle of the shapes between recursive calls to drawFractal(). We’ll cover these specific details later in this chapter, but let’s look at one example: fractal 7, which draws a wave-like image.
The program produces the Wave fractal by calling the drawTriangleOutline() shape-drawing function, which creates a single triangle. The additional arguments to drawFractal() tell it to make three recursive calls to drawFractal(). Figure 13-3 shows the triangle produced by the original call to drawFractal() and the triangles produced by the three recursive calls.

Figure 13-3: The triangle produced by the first call to drawFractal() (left) and the first set of three recursive calls (right)
The first recursive call tells drawFractal() to call drawTriangleOutline() but with a triangle that is half the size and positioned to the top left of the previous triangle. The second recursive call produces a triangle to the top right of the previous triangle that is 30 percent of its size. The third recursive call produces a triangle below the previous triangle that is half its size and rotated 15 degrees compared to it.
Each of these three recursive calls to drawFractal() makes three more recursive calls to drawFractal(), producing nine new triangles. The new triangles have the same changes to their size, position, and angle relative to their previous triangle. The top-left triangle is always half the size of the previous triangle, while the bottom triangle is always rotated 15 degrees more. Figure 13-4 shows the triangles produced by the first and second levels of recursion.

Figure 13-4: The first level of recursive calls to drawFractal() (left) and the nine new triangles of the second level of recursive calls (right)
The nine calls to drawFractal() that produce these nine new triangles each make three recursive calls to drawFractal(), producing 27 new triangles at the next level of recursion. As this pattern of recursion continues, eventually the triangles become so small that drawFractal() stops making new recursive calls. This is one of the base cases for the recursive drawFractal() function. The other occurs when the recursive depth reaches a specified level. Either way, these recursive calls produce the final Wave fractal in Figure 13-5.
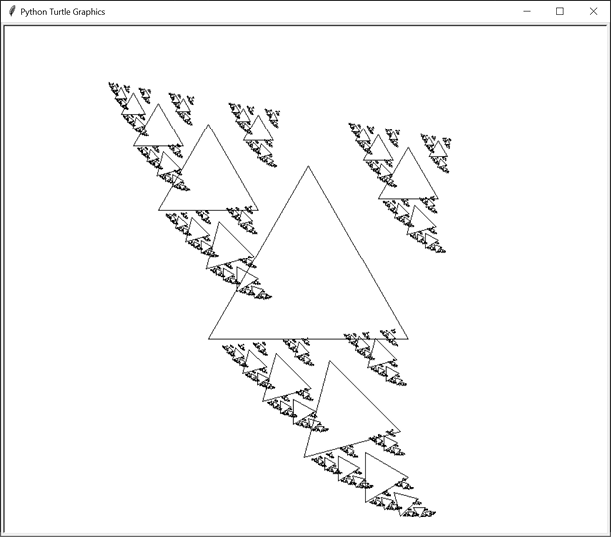
Figure 13-5: The final Wave fractal after each triangle recursively generates three more triangles
The nine example fractals in Figure 13-1 that come with the Fractal Art Maker are made with just two shape-drawing functions and a few changes to the arguments to drawFractal(). Let’s take a look at the Fractal Art Maker’s code to see how it accomplishes this.
Enter the following code into a new file and save it as fractalArtMaker.py. This program relies on Python’s built-in turtle module, so no JavaScript code is used for this chapter’s project:
Python
import turtle, math
DRAW_FRACTAL = 1 # Set to 1 through 11 and run the program.
turtle.tracer(5000, 0) # Increase the first argument to speed up the drawing.
turtle.hideturtle()
def drawFilledSquare(size, depth):
size = int(size)
# Move to the top-right corner before drawing:
turtle.penup()
turtle.forward(size // 2)
turtle.left(90)
turtle.forward(size // 2)
turtle.left(180)
turtle.pendown()
# Alternate between white and gray (with black border):
if depth % 2 == 0:
turtle.pencolor('black')
turtle.fillcolor('white')
else:
turtle.pencolor('black')
turtle.fillcolor('gray')
# Draw a square:
turtle.begin_fill()
for i in range(4): # Draw four lines.
turtle.forward(size)
turtle.right(90)
turtle.end_fill()
def drawTriangleOutline(size, depth):
size = int(size)
# Move the turtle to the top of the equilateral triangle:
height = size * math.sqrt(3) / 2
turtle.penup()
turtle.left(90) # Turn to face upward.
turtle.forward(height * (2/3)) # Move to the top corner.
turtle.right(150) # Turn to face the bottom-right corner.
turtle.pendown()
# Draw the three sides of the triangle:
for i in range(3):
turtle.forward(size)
turtle.right(120)
def drawFractal(shapeDrawFunction, size, specs, maxDepth=8, depth=0):
if depth > maxDepth or size < 1:
return # BASE CASE
# Save the position and heading at the start of this function call:
initialX = turtle.xcor()
initialY = turtle.ycor()
initialHeading = turtle.heading()
# Call the draw function to draw the shape:
turtle.pendown()
shapeDrawFunction(size, depth)
turtle.penup()
# RECURSIVE CASE
for spec in specs:
# Each dictionary in specs has keys 'sizeChange', 'xChange',
# 'yChange', and 'angleChange'. The size, x, and y changes
# are multiplied by the size parameter. The x change and y
# change are added to the turtle's current position. The angle
# change is added to the turtle's current heading.
sizeCh = spec.get('sizeChange', 1.0)
xCh = spec.get('xChange', 0.0)
yCh = spec.get('yChange', 0.0)
angleCh = spec.get('angleChange', 0.0)
# Reset the turtle to the shape's starting point:
turtle.goto(initialX, initialY)
turtle.setheading(initialHeading + angleCh)
turtle.forward(size * xCh)
turtle.left(90)
turtle.forward(size * yCh)
turtle.right(90)
# Make the recursive call:
drawFractal(shapeDrawFunction, size * sizeCh, specs, maxDepth,
depth + 1)
if DRAW_FRACTAL == 1:
# Four Corners:
drawFractal(drawFilledSquare, 350,
[{'sizeChange': 0.5, 'xChange': -0.5, 'yChange': 0.5},
{'sizeChange': 0.5, 'xChange': 0.5, 'yChange': 0.5},
{'sizeChange': 0.5, 'xChange': -0.5, 'yChange': -0.5},
{'sizeChange': 0.5, 'xChange': 0.5, 'yChange': -0.5}], 5)
elif DRAW_FRACTAL == 2:
# Spiral Squares:
drawFractal(drawFilledSquare, 600, [{'sizeChange': 0.95,
'angleChange': 7}], 50)
elif DRAW_FRACTAL == 3:
# Double Spiral Squares:
drawFractal(drawFilledSquare, 600,
[{'sizeChange': 0.8, 'yChange': 0.1, 'angleChange': -10},
{'sizeChange': 0.8, 'yChange': -0.1, 'angleChange': 10}])
elif DRAW_FRACTAL == 4:
# Triangle Spiral:
drawFractal(drawTriangleOutline, 20,
[{'sizeChange': 1.05, 'angleChange': 7}], 80)
elif DRAW_FRACTAL == 5:
# Conway's Game of Life Glider:
third = 1 / 3
drawFractal(drawFilledSquare, 600,
[{'sizeChange': third, 'yChange': third},
{'sizeChange': third, 'xChange': third},
{'sizeChange': third, 'xChange': third, 'yChange': -third},
{'sizeChange': third, 'yChange': -third},
{'sizeChange': third, 'xChange': -third, 'yChange': -third}])
elif DRAW_FRACTAL == 6:
# Sierpiński Triangle:
toMid = math.sqrt(3) / 6
drawFractal(drawTriangleOutline, 600,
[{'sizeChange': 0.5, 'yChange': toMid, 'angleChange': 0},
{'sizeChange': 0.5, 'yChange': toMid, 'angleChange': 120},
{'sizeChange': 0.5, 'yChange': toMid, 'angleChange': 240}])
elif DRAW_FRACTAL == 7:
# Wave:
drawFractal(drawTriangleOutline, 280,
[{'sizeChange': 0.5, 'xChange': -0.5, 'yChange': 0.5},
{'sizeChange': 0.3, 'xChange': 0.5, 'yChange': 0.5},
{'sizeChange': 0.5, 'yChange': -0.7, 'angleChange': 15}])
elif DRAW_FRACTAL == 8:
# Horn:
drawFractal(drawFilledSquare, 100,
[{'sizeChange': 0.96, 'yChange': 0.5, 'angleChange': 11}], 100)
elif DRAW_FRACTAL == 9:
# Snowflake:
drawFractal(drawFilledSquare, 200,
[{'xChange': math.cos(0 * math.pi / 180),
'yChange': math.sin(0 * math.pi / 180), 'sizeChange': 0.4},
{'xChange': math.cos(72 * math.pi / 180),
'yChange': math.sin(72 * math.pi / 180), 'sizeChange': 0.4},
{'xChange': math.cos(144 * math.pi / 180),
'yChange': math.sin(144 * math.pi / 180), 'sizeChange': 0.4},
{'xChange': math.cos(216 * math.pi / 180),
'yChange': math.sin(216 * math.pi / 180), 'sizeChange': 0.4},
{'xChange': math.cos(288 * math.pi / 180),
'yChange': math.sin(288 * math.pi / 180), 'sizeChange': 0.4}])
elif DRAW_FRACTAL == 10:
# The filled square shape:
turtle.tracer(1, 0)
drawFilledSquare(400, 0)
elif DRAW_FRACTAL == 11:
# The triangle outline shape:
turtle.tracer(1, 0)
drawTriangleOutline(400, 0)
else:
assert False, 'Set DRAW_FRACTAL to a number from 1 to 11.'
turtle.exitonclick() # Click the window to exit.When you run this program, it will show the first of nine fractal images from Figure 13-1. You can change the DRAW_FRACTAL constant at the beginning of the source code to any integer from 1 to 9 and run the program again to see a new fractal. After learning how the program works, you’ll also be able to create your own shape-drawing functions and call drawFractal() to produce fractals of your own design.
The first lines of the program cover basic setup steps for our turtle-based program:
Python
import turtle, math
DRAW_FRACTAL = 1 # Set to 1 through 11 and run the program.
turtle.tracer(5000, 0) # Increase the first argument to speed up the drawing.
turtle.hideturtle()The program imports the turtle module for drawing. It also imports the math module for the math.sqrt() function, which the Sierpiński Triangle fractal will use, and the math.cos() and math.sin() functions, for the Snowflake fractal.
The DRAW_FRACTAL constant can be set to any integer from 1 to 9 to draw one of the nine built-in fractals the program produces. You can also set it to 10 or 11 to show the output of the square or triangle shape-drawing function, respectively.
We also call some turtle functions to prepare for drawing. The turtle.tracer(5000, 0) call speeds up the drawing of the fractal. The 5000 argument tells the turtle module to wait until 5,000 turtle drawing instructions have been processed before rendering the drawing on the screen, and the 0 argument tells it to pause for 0 milliseconds after each drawing instruction. Otherwise, the turtle module would render the image after each drawing instruction, which significantly slows the program if we want only the final image.
You can change this call to turtle.tracer(1, 10) if you want to slow the drawing and watch the lines as they’re produced. This can be useful when making your own fractals to debug any problems with the drawing.
The turtle.hideturtle() call hides the triangle shape on the screen that represents the turtle’s current position and heading. (Heading is another term for direction.) We call this function so that the marker doesn’t appear in the final image.
The drawFractal() function uses a shape-drawing function passed to it to draw the individual parts of the fractal. This is usually a simple shape, such as a square or triangle. The beautiful complexity of the fractals emerges from drawFractal() recursively calling this function for each individual component of the whole fractal.
The shape-drawing functions for the Fractal Art Maker have two parameters: size and depth. The size parameter is the length of the sides of the square or triangle it draws. The shape-drawing functions should always use arguments to turtle.forward() that are based on size so that the lengths will be proportionate to size at each level of recursion. Avoid code like turtle.forward(100) or turtle.forward(200); instead, use code that is based on the size parameter, like turtle.forward(size) or turtle.forward(size * 2). In Python’s turtle module, turtle.forward(1) moves the turtle by one unit, which is not necessarily the same as one pixel.
The shape-drawing functions’ second parameter is the recursive depth of drawFractal(). The original call to drawFractal() has the depth parameter set to 0. Recursive calls to drawFractal() use depth + 1 as the depth parameter. In the Wave fractal, the first triangle in the center of the window has a depth argument of 0. The three triangles created next have a depth of 1. The nine triangles around those three triangles have a depth of 2, and so on.
Your shape-drawing function can ignore this argument, but using it can cause interesting variations to the basic shape. For example, the drawFilledSquare() shape-drawing function uses depth to alternate between drawing white squares and gray squares. Keep this in mind if you’d like to create your own shape-drawing functions for the Fractal Art Maker program, as they must accept a size and depth argument.
The drawFilledSquare() function draws a filled-in square with sides of length size. To color the square, we use the turtle module’s turtle.begin_fill() and turtle.end_fill() functions to make the square either white or gray, with a black border, depending on whether the depth argument is even or odd. Because these squares are filled in, any squares drawn on top of them later will cover them.
Like all shape-drawing functions for the Fractal Art Maker program, drawFilledSquare() accepts a size and depth parameter:
def drawFilledSquare(size, depth):
size = int(size)The size argument could be a floating-point number with a fractional part, which sometimes causes the turtle module to make slightly asymmetrical and uneven drawings. To prevent this, the first line of the function rounds size down to an integer.
When the function draws the square, it assumes the turtle is in the center of the square. Thus, the turtle must first move to the top-right corner of the square, relative to its initial heading:
Python
# Move to the top-right corner before drawing:
turtle.penup()
turtle.forward(size // 2)
turtle.left(90)
turtle.forward(size // 2)
turtle.left(180)
turtle.pendown()The drawFractal() function always has the pen down and ready to draw when the shape-drawing function is called, so drawFilledSquare() must call turtle.penup() to avoid drawing a line as it moves to the starting position. To find the starting position relative to the middle of the square, the turtle must first move half of the square’s length (that is, size // 2) forward, to the future right edge of the square. Next the turtle turns 90 degrees to face up and then moves size // 2 units forward to the top-right corner. The turtle is now facing the wrong way, so it turns around 180 degrees and places the pen down so that it can begin drawing.
Note that top-right and up are relative to the direction the turtle is originally facing. This code works just as well if the turtle begins facing to the right at 0 degrees or has a heading of 90, 42, or any other number of degrees. When you create your own shape-drawing functions, stick to the relative turtle movement functions like turtle.forward(), turtle.left(), and turtle.right() instead of absolute turtle movement functions like turtle.goto().
Next, the depth argument tells the function whether it should draw a white square or a gray one:
Python
# Alternate between white and gray (with black border):
if depth % 2 == 0:
turtle.pencolor('black')
turtle.fillcolor('white')
else:
turtle.pencolor('black')
turtle.fillcolor('gray')If depth is even, the depth % 2 == 0 condition is True, and the square’s fill color is white. Otherwise, the code sets the fill color to gray. Either way, the border of the square, determined by the pen color, is set to black. To change either of these colors, use strings of common color names, like red or yellow, or an HTML color code comprising a hash mark and six hexadecimal digits, like #24FF24 for lime green or #AD7100 for brown.
The website https://html-color.codes has charts for many HTML color codes. The fractals in this black-and-white book lack color, but your computer can render your own fractals in a bright range of colors!
With the colors set, we can finally draw the four lines of the actual square:
Python
# Draw a square:
turtle.begin_fill()
for i in range(4): # Draw four lines.
turtle.forward(size)
turtle.right(90)
turtle.end_fill()To tell the turtle module that we intend to draw a filled-in shape and not just the outline, we call the turtle.begin_fill() function. Next is a for loop that draws a line of length size and turns the turtle 90 degrees to the right. The for loop repeats this four times to create the square. When the function finally calls turtle.end_fill(), the filled-in square appears on the screen.
The second shape-drawing function draws the outline of an equilateral triangle whose sides have a length of size. The function draws the triangle oriented with one corner at the top and two corners at the bottom. Figure 13-6 illustrates the various dimensions of an equilateral triangle.
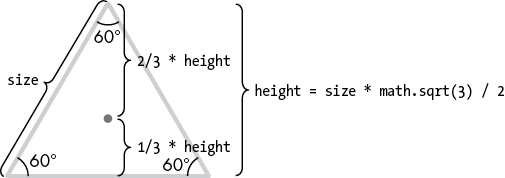
Figure 13-6: The measurements of an equilateral triangle with sides the length of size
Before we begin drawing, we must determine the triangle’s height based on the length of its sides. Geometry tells us that, for equilateral triangles with sides of length L, the height h of the triangle is L times the square root of 3 divided by 2. In our function, L corresponds to the size parameter, so our code sets the height variable as follows:
height = size * math.sqrt(3) / 2Geometry also tells us that the center of the triangle is one-third of the height from the bottom side and two-thirds of the height from the top point. This gives us the information we need to move the turtle to its starting position:
Python
def drawTriangleOutline(size, depth):
size = int(size)
# Move the turtle to the top of the equilateral triangle:
height = size * math.sqrt(3) / 2
turtle.penup()
turtle.left(90) # Turn to face upward.
turtle.forward(height * (2/3)) # Move to the top corner.
turtle.right(150) # Turn to face the bottom-right corner.
turtle.pendown()To reach the top corner, we turn the turtle 90 degrees left to face up (relative to the turtle’s original heading right at 0 degrees) and then move forward a number of units equal to height * (2/3). The turtle is still facing up, so to begin drawing the line on the right side, the turtle must turn 90 degrees right to face rightward, then an additional 60 degrees to face the bottom-right corner of the triangle. This is why we call turtle.right(150).
At this point, the turtle is ready to start drawing the triangle, so we lower the pen by calling turtle.pendown(). A for loop will handle drawing the three sides:
Python
# Draw the three sides of the triangle:
for i in range(3):
turtle.forward(size)
turtle.right(120)Drawing the actual triangle is a matter of moving forward by size units, and then turning 120 degrees to the right, three separate times. The third and final 120-degree turn leaves the turtle facing its original direction. You can see these movements and turns in Figure 13-7.
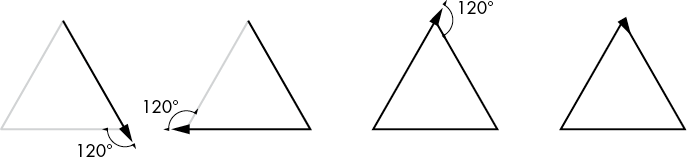
Figure 13-7: Drawing an equilateral triangle involves three forward movements and three 120-degree turns.
The drawTriangleOutline() function draws only the outline and not a filled-in shape, so it doesn’t call turtle.begin_fill() and turtle.end_fill() as drawFilledSquare() does.
Now that we have two sample drawing functions to work with, let’s examine the main function in the Fractal Art Maker project, drawFractal(). This function has three required parameters and one optional one: shapeDrawFunction, size, specs, and maxDepth.
The shapeDrawFunction parameter expects a function, like drawFilledSquare() or drawTriangleOutline(). The size parameter expects the starting size passed to the drawing function. Often, a value between 100 and 500 is a good starting size, though this depends on the code in your shape-drawing function, and finding the right value may require experimentation.
The specs parameter expects a list of dictionaries that specify how the recursive shapes should change their size, position, and angle as drawFractal() recursively calls itself. These specifications are described later in this section.
To prevent drawFractal() from recursing until it causes a stack overflow, the maxDepth parameter holds the number of times drawFractal() should recursively call itself. By default, maxDepth has a value of 8, but you can provide a different value if you want more or fewer recursive shapes.
A fifth parameter, depth, is handled by drawFractal()’s recursive call to itself and defaults to 0. You don’t need to specify it when you call drawFractal().
The first thing the drawFractal() function does is check for its two base cases:
Python
def drawFractal(shapeDrawFunction, size, specs, maxDepth=8, depth=0):
if depth > maxDepth or size < 1:
return # BASE CASEIf depth is greater than maxDepth, the function will stop the recursion and return. The other base case occurs if size is less than 1, at which point the shapes being drawn would be too small to be seen on the screen and so the function should simply return.
We keep track of the turtle’s original position and heading in three variables: initialX, initialY, and initialHeading. This way, no matter where the shape-drawing function leaves the turtle positioned or what direction it is headed, drawFractal() can revert the turtle back to the original position and heading for the next recursive call:
Python
# Save the position and heading at the start of this function call:
initialX = turtle.xcor()
initialY = turtle.ycor()
initialHeading = turtle.heading()The turtle.xcor() and turtle.ycor() functions return the absolute x- and y-coordinates of the turtle on the screen. The turtle.heading() function returns the direction in which the turtle is pointed in degrees.
The next few lines call the shape-drawing function passed to the shapeDrawFunction parameter:
Python
# Call the draw function to draw the shape:
turtle.pendown()
shapeDrawFunction(size, depth)
turtle.penup()Because the value passed as the argument for the shapeDrawFunction parameter is a function, the code shapeDrawFunction(size, depth) calls this function with the values in size and depth. The pen is lowered before and raised after the shapeDrawFunction() call to ensure that the shape-drawing function can consistently expect the pen to be down when the drawing begins.
After the call to shapeDrawFunction(), the rest of drawFractal()’s code is devoted to making recursive calls to drawFractal() based on the specification in the specs list’s dictionaries. For each dictionary, drawFractal() makes one recursive call to drawFractal(). If specs is a list with one dictionary, every call to drawFractal() results in only one recursive call to drawFractal(). If specs is a list with three dictionaries, every call to drawFractal() results in three recursive calls to drawFractal().
The dictionaries in the specs parameter provide specifications for each recursive call. Each of these dictionaries has the keys sizeChange, xChange, yChange, and angleChange. These dictate how the size of the fractal, the position of the turtle, and the heading of the turtle change for a recursive drawFractal() call. Table 13-1 describes the four keys in a specification.
Table 13-1: Keys in the Specification Dictionaries
| Key | Default value | Description |
sizeChange |
1.0 |
The next recursive shape’s size value is the current size multiplied by this value. |
xChange |
0.0 |
The next recursive shape’s x-coordinate is the current x-coordinate plus the current size multiplied by this value. |
yChange |
0.0 |
The next recursive shape’s y-coordinate is the current y-coordinate plus the current size multiplied by this value. |
angleChange |
0.0 |
The next recursive shape’s starting angle is the current starting angle plus this value, in degrees. |
Let’s take a look at the specification dictionary for the Four Corners fractal, which produces the top-left image shown previously in Figure 13-1. The call to drawFractal() for the Four Corners fractal passes the following list of dictionaries for the specs parameter:
Python
[{'sizeChange': 0.5, 'xChange': -0.5, 'yChange': 0.5},
{'sizeChange': 0.5, 'xChange': 0.5, 'yChange': 0.5},
{'sizeChange': 0.5, 'xChange': -0.5, 'yChange': -0.5},
{'sizeChange': 0.5, 'xChange': 0.5, 'yChange': -0.5}]The specs list has four dictionaries, so each call to drawFractal() that draws a square will, in turn, recursively call drawFractal() four more times to draw four more squares. Figure 13-8 shows this progression of squares (which alternate between white and gray).
To determine the size of the next square to be drawn, the value for the sizeChange key is multiplied by the current size parameter. The first dictionary in the specs list has a sizeChange value of 0.5, which makes the next recursive call have a size argument of 350 * 0.5, or 175 units. This makes the next square half the size of the previous square. A sizeChange value of 2.0 would, for example, double the size of the next square. If the dictionary has no sizeChange key, the value defaults to 1.0 for no change to the size.
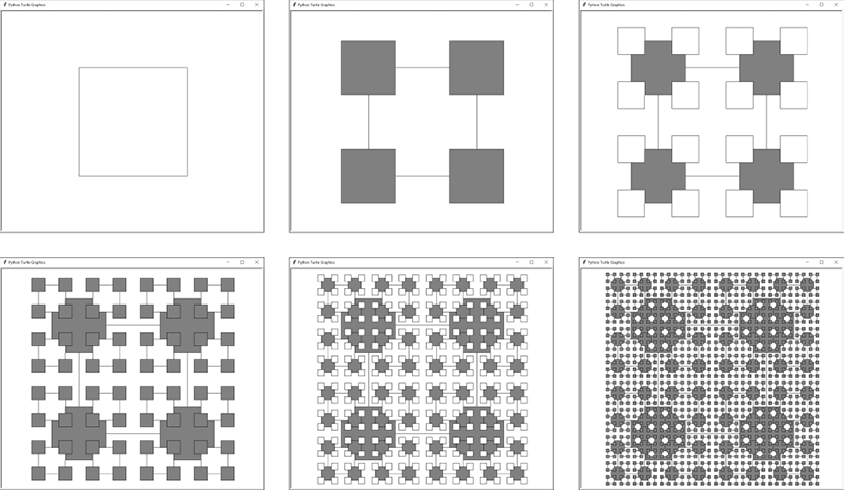
Figure 13-8: Each step of the Four Corners example from left to right, top to bottom. Each square recursively produces four more squares at its corners, with colors alternating between white and gray.
To determine the x-coordinate of the next square, the first dictionary’s xChange value, -0.5 in this case, is multiplied by the size. When size is 350, this means the next square has an x-coordinate of -175 units relative to the turtle’s current position. This xChange value and the yChange key’s value of 0.5 places the next square’s position a distance of 50 percent of the current square’s size, to the left and above the current square’s position. This happens to center it on the top-left corner of the current square.
If you look at the three other dictionaries in the specs list, you’ll notice they all have a sizeChange value of 0.5. The difference between them is that their xChange and yChange values place them in the other three corners of the current square. As a result, the next four squares are drawn centered on the four corners of the current square.
The dictionaries in the specs list for this example don’t have an angleChange value, so this value defaults to 0.0 degrees. A positive angleChange value indicates a counterclockwise rotation, while a negative value indicates a clockwise rotation.
Each dictionary represents a separate square to be drawn each time the recursive function is called. If we were to remove the first dictionary from the specs list, each drawFractal() call would produce only three squares, as in Figure 13-9.
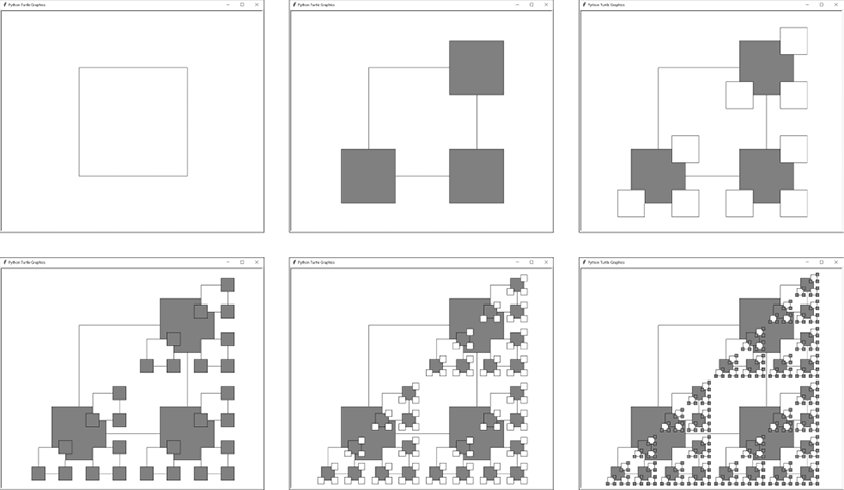
Figure 13-9: The Four Corners fractal with the first dictionary removed from the specs list
Let’s look at how the code in drawFractal() actually does everything we’ve described:
Python
# RECURSIVE CASE
for spec in specs:
# Each dictionary in specs has keys 'sizeChange', 'xChange',
# 'yChange', and 'angleChange'. The size, x, and y changes
# are multiplied by the size parameter. The x change and y
# change are added to the turtle's current position. The angle
# change is added to the turtle's current heading.
sizeCh = spec.get('sizeChange', 1.0)
xCh = spec.get('xChange', 0.0)
yCh = spec.get('yChange', 0.0)
angleCh = spec.get('angleChange', 0.0)The for loop assigns an individual specification dictionary in the specs list to the loop variable spec on each iteration of the loop. The get() dictionary method calls pull the values for the sizeChange, xChange, yChange, and angleChange keys from this dictionary and assign them to the shorter-named sizeCh, xCh, yCh, and angleCh variables. The get() method substitutes a default value if the key doesn’t exist in the dictionary.
Next, the turtle’s position and heading are reset to the values indicated when drawFractal() was first called. This ensures that the recursive calls from previous loop iterations don’t leave the turtle in some other place. Then the heading and position are changed according to the angleCh, xCh, and yCh variables:
Python
# Reset the turtle to the shape's starting point:
turtle.goto(initialX, initialY)
turtle.setheading(initialHeading + angleCh)
turtle.forward(size * xCh)
turtle.left(90)
turtle.forward(size * yCh)
turtle.right(90)The x-change and y-change positions are expressed relative to the turtle’s current heading. If the turtle’s heading is 0, the turtle’s relative x-axis is the same as the actual x-axis on the screen. However, if the turtle’s heading is, say, 45, the turtle’s relative x-axis is at a 45-degree tilt. Moving “right” along the turtle’s relative x-axis would then move at an up-right angle.
This is why moving forward by size * xCh moves the turtle along its relative x-axis. If xCh is negative, turtle.forward() moves left along the turtle’s relative x-axis. The turtle.left(90) call points the turtle along the turtle’s relative y-axis, and turtle.forward(size * yCh) moves the turtle to the next shape’s starting position. However, the turtle.left(90) call changed the turtle’s heading, so turtle.right(90) is called to reset it back to its original direction.
Figure 13-10 shows how these four lines of code move the turtle to the right along its relative x-axis and up along its relative y-axis and leave it in the correct heading, no matter what its initial heading was.
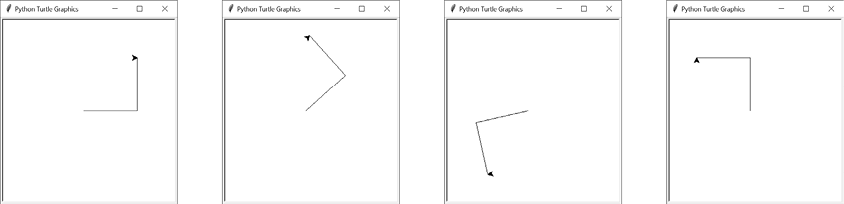
Figure 13-10: In each of these four images, the turtle always moves 100 units “right” and “up” along the relative x-axis and y-axis of its initial heading.
Finally, with the turtle in the correct position and heading for the next shape, we make the recursive call to drawFractal():
Python
# Make the recursive call:
drawFractal(shapeDrawFunction, size * sizeCh, specs, maxDepth,
depth + 1)The shapeDrawFunction, specs, and maxDepth arguments are passed to the recursive drawFractal() call unchanged. However, size * sizeCh is passed for the next size parameter to reflect the change in the size of the recursive shape, and depth + 1 is passed for the depth parameter to increment it for the next shape-drawing function call.
Now that we’ve covered how the shape-drawing functions and recursive drawFractal() function work, let’s look at the nine example fractals that come with the Fractal Art Maker. You can see these examples in Figure 13-1.
The first fractal is Four Corners, which begins as a large square. As the function calls itself, the fractal’s specifications cause four smaller squares to be drawn in the four corners of the square:
Python
if DRAW_FRACTAL == 1:
# Four Corners:
drawFractal(drawFilledSquare, 350,
[{'sizeChange': 0.5, 'xChange': -0.5, 'yChange': 0.5},
{'sizeChange': 0.5, 'xChange': 0.5, 'yChange': 0.5},
{'sizeChange': 0.5, 'xChange': -0.5, 'yChange': -0.5},
{'sizeChange': 0.5, 'xChange': 0.5, 'yChange': -0.5}], 5)The call to drawFractal() here limits the maximum depth to 5, as any more tends to make the fractal so dense that the fine detail becomes hard to see. This fractal appears in Figure 13-8.
The Spiral Squares fractal also starts as a large square, but it creates just one new square on each recursive call:
Python
elif DRAW_FRACTAL == 2:
# Spiral Squares:
drawFractal(drawFilledSquare, 600, [{'sizeChange': 0.95,
'angleChange': 7}], 50)This square is slightly smaller and rotated by 7 degrees. The centers of all the squares are unchanged, so there’s no need to add xChange and yChange keys to the specification. The default maximum depth of 8 is too small to get an interesting fractal, so we increase it to 50 to produce a hypnotic spiral pattern.
The Double Spiral Squares fractal is similar to Spiral Squares, except each square creates two smaller squares. This creates an interesting fan effect, as the second square is drawn later and tends to cover up previously drawn squares:
Python
elif DRAW_FRACTAL == 3:
# Double Spiral Squares:
drawFractal(drawFilledSquare, 600,
[{'sizeChange': 0.8, 'yChange': 0.1, 'angleChange': -10},
{'sizeChange': 0.8, 'yChange': -0.1, 'angleChange': 10}])The squares are created slightly higher or lower than their previous square and rotated either 10 or -10 degrees.
The Triangle Spiral fractal, another variation of Spiral Squares, uses the drawTriangleOutline() shape-drawing function instead of drawFilledSquare():
Python
elif DRAW_FRACTAL == 4:
# Triangle Spiral:
drawFractal(drawTriangleOutline, 20,
[{'sizeChange': 1.05, 'angleChange': 7}], 80)Unlike the Spiral Squares fractal, the Triangle Spiral fractal begins at the small size of 20 units and slightly increases in size for each level of recursion. The sizeChange key is greater than 1.0, so the shapes are always increasing in size. This means the base case occurs when the recursion reaches a depth of 80, because the base case of size becoming less than 1 is never reached.
Conway’s Game of Life is a famous example of cellular automata. The game’s simple rules cause interesting and wildly chaotic patterns to emerge on a 2D grid. One such pattern is a Glider consisting of five cells in a 3 × 3 space:
Python
elif DRAW_FRACTAL == 5:
# Conway's Game of Life Glider:
third = 1 / 3
drawFractal(drawFilledSquare, 600,
[{'sizeChange': third, 'yChange': third},
{'sizeChange': third, 'xChange': third},
{'sizeChange': third, 'xChange': third, 'yChange': -third},
{'sizeChange': third, 'yChange': -third},
{'sizeChange': third, 'xChange': -third, 'yChange': -third}])The Glider fractal here has additional Gliders drawn inside each of its five cells. The third variable helps precisely set the position of the recursive shapes in the 3 × 3 space.
You can find a Python implementation of Conway’s Game of Life in my book The Big Book of Small Python Projects (No Starch Press, 2021) and online at https://inventwithpython.com/bigbookpython/project13.html. Tragically, John Conway, the mathematician and professor who developed Conway’s Game of Life, passed away of complications from COVID-19 in April 2020.
We created the Sierpiński Triangle fractal in Chapter 9, but our Fractal Art Maker can re-create it as well by using the drawTriangleOutline() shape function. After all, a Sierpiński triangle is an equilateral triangle with three smaller equilateral triangles drawn in its interior:
Python
elif DRAW_FRACTAL == 6:
# Sierpiński Triangle:
toMid = math.sqrt(3) / 6
drawFractal(drawTriangleOutline, 600,
[{'sizeChange': 0.5, 'yChange': toMid, 'angleChange': 0},
{'sizeChange': 0.5, 'yChange': toMid, 'angleChange': 120},
{'sizeChange': 0.5, 'yChange': toMid, 'angleChange': 240}])The center of these smaller triangles is size * math.sqrt(3) / 6 units from the center of the previous triangle. The three calls adjust the heading of the turtle to 0, 120, and 240 degrees before moving up on the turtle’s relative y-axis.
We discussed the Wave fractal at the start of this chapter, and you can see it in Figure 13-5. This relatively simple fractal creates three smaller and distinct recursive triangles:
Python
elif DRAW_FRACTAL == 7:
# Wave:
drawFractal(drawTriangleOutline, 280,
[{'sizeChange': 0.5, 'xChange': -0.5, 'yChange': 0.5},
{'sizeChange': 0.3, 'xChange': 0.5, 'yChange': 0.5},
{'sizeChange': 0.5, 'yChange': -0.7, 'angleChange': 15}])The Horn fractal resembles a ram’s horn:
Python
elif DRAW_FRACTAL == 8:
# Horn:
drawFractal(drawFilledSquare, 100,
[{'sizeChange': 0.96, 'yChange': 0.5, 'angleChange': 11}], 100)This simple fractal is made up of squares, each of which is slightly smaller, moved up, and rotated 11 degrees from the previous square. We increase the maximum recursion depth to 100 to extend the horn into a tight spiral.
The final fractal, Snowflake, is composed of squares laid out in a pentagon pattern. This is similar to the Four Corners fractal, but it uses five evenly spaced recursive squares instead of four:
Python
elif DRAW_FRACTAL == 9:
# Snowflake:
drawFractal(drawFilledSquare, 200,
[{'xChange': math.cos(0 * math.pi / 180),
'yChange': math.sin(0 * math.pi / 180), 'sizeChange': 0.4},
{'xChange': math.cos(72 * math.pi / 180),
'yChange': math.sin(72 * math.pi / 180), 'sizeChange': 0.4},
{'xChange': math.cos(144 * math.pi / 180),
'yChange': math.sin(144 * math.pi / 180), 'sizeChange': 0.4},
{'xChange': math.cos(216 * math.pi / 180),
'yChange': math.sin(216 * math.pi / 180), 'sizeChange': 0.4},
{'xChange': math.cos(288 * math.pi / 180),
'yChange': math.sin(288 * math.pi / 180), 'sizeChange': 0.4}])This fractal uses the cosine and sine functions from trigonometry, implemented in Python’s math.cos() and math.sin() functions, to determine how to shift the squares along the x-axis and y-axis. A full circle has 360 degrees, so to evenly space out the five recursive squares in this circle, we place them at intervals of 0, 72, 144, 216, and 288 degrees. The math.cos() and math.sin() functions expect the angle argument to be in radians instead of degrees, so we must multiply these numbers by math.pi / 180.
The end result is that each square is surrounded by five other squares, which are surrounded by five other squares, and so on, to form a crystal-like fractal that resembles a snowflake.
For completion, you can also set DRAW_FRACTAL to 10 or 11 to view what a single call to drawFilledSquare() and drawTriangleOutline() produce in the turtle window. These shapes are drawn with a size of 600:
Python
elif DRAW_FRACTAL == 10:
# The filled square shape:
turtle.tracer(1, 0)
drawFilledSquare(400, 0)
elif DRAW_FRACTAL == 11:
# The triangle outline shape:
turtle.tracer(1, 0)
drawTriangleOutline(400, 0)
turtle.exitonclick() # Click the window to exit.After drawing the fractal or shape based on the value in DRAW_FRACTAL, the program calls turtle.exitonclick() so that the turtle window stays open until the user clicks it. Then the program terminates.
You can create your own fractals by changing the specification passed to the drawFractal() function. Start by thinking about how many recursive calls you’d like each call to drawFractal() to generate, and how the size, position, and heading of the shapes should change. You can use the existing shape-drawing functions or create your own.
For example, Figure 13-11 shows the nine built-in fractals, except the square and triangle functions have been swapped. Some of these produce bland shapes, but others can result in unexpected beauty.

Figure 13-11: The nine fractals that come with Fractal Art Maker, with the shape-drawing functions swapped
The Fractal Art Maker projects demonstrate the endless possibilities of recursion. A simple recursive drawFractal() function, paired with a shape-drawing function, can create a large variety of detailed geometric art.
At the core of Fractal Art Maker is the recursive drawFractal() function, which accepts another function as an argument. This second function draws a basic shape repeatedly by using the size, position, and heading given in the list of specification dictionaries.
You can test an unlimited number of shape-drawing functions and specification settings. Let your creativity drive your fractal projects as you experiment with the code in this program.
There are websites that allow you to create fractals. Interactive Fractal Tree at https://www.visnos.com/demos/fractal has sliders to change a binary tree fractal’s angle and size parameters. Procedural Snowflake at https://procedural-snowflake.glitch.me generates new snowflakes in your browser. Nico’s Fractal Machine at https://sciencevsmagic.net/fractal creates animated drawings of fractals. You can find others by searching the web for fractal maker or fractal generator online.