Check out other books by Al Sweigart, free online or available for purchase:




...and other books as well! Or register for the online video course. You can also donate to support the author directly.





If you take a computer science course, the unit on recursion is sure to cover some of the classic algorithms presented in this chapter. Coding interviews (which, for lack of suitable ways to evaluate candidates, often crib notes from freshman computer science curricula) can touch upon them too. This chapter covers six classic problems in recursion, along with their solutions.
We begin with three simple algorithms: summing the numbers in an array, reversing a text string, and detecting whether a string is a palindrome. Then we explore an algorithm for solving the Tower of Hanoi puzzle, implement the flood fill drawing algorithm, and tackle the absurdly recursive Ackermann function.
In the process, you’ll learn about the head-tail technique for splitting up the data in the recursive function arguments. We’ll also ask ourselves three questions when trying to come up with recursive solutions: What is the base case? What argument is passed to the recursive function call? And how do the arguments passed to the recursive function calls become closer to the base case? As you gain more experience, answering these questions should come more naturally.
Our first example is simple: given a list (in Python) or an array (in JavaScript) of integers, return the total sum of all the integers. For example, a call such as sum([5, 2, 4, 8]) should return 19.
This is easy to solve with a loop, but solving it with recursion requires more thought. After reading Chapter 2, you might also notice that this algorithm doesn’t map well enough to recursion’s capabilities to justify recursion’s added complexity. Still, summing numbers in an array (or some other calculation based on processing data in a linear data structure) is a common enough recursion problem in coding interviews that it deserves our attention.
To solve this problem, let’s examine the head-tail technique for implementing recursive functions. This technique splits the recursive function’s array argument into two parts: the head (the first element of the array) and the tail (a new array including everything after the first element). We define the recursive sum() function to find the sum of the array argument’s integers by adding the head to the sum of the tail array. To find out the sum of the tail array, we recursively pass it as the array argument to sum().
Because the tail array is one element smaller than the original array argument, we’ll eventually end up calling the recursive function and passing it an empty array. An empty array argument is trivial to sum and doesn’t require more recursive calls; it is merely 0. From these facts, our answers to the three questions are as follows:
0.Here is sumHeadTail.py, a Python program to sum a list of numbers:
Python
def sum(numbers):
if len(numbers) == 0: # BASE CASE
❶ return 0
else: # RECURSIVE CASE
❷ head = numbers[0]
❸ tail = numbers[1:]
❹ return head + sum(tail)
nums = [1, 2, 3, 4, 5]
print('The sum of', nums, 'is', sum(nums))
nums = [5, 2, 4, 8]
print('The sum of', nums, 'is', sum(nums))
nums = [1, 10, 100, 1000]
print('The sum of', nums, 'is', sum(nums))
And here is the equivalent JavaScript program, sumHeadTail.html:
JavaScript
<script type="text/javascript">
function sum(numbers) {
if (numbers.length === 0) { // BASE CASE
❶ return 0;
} else { // RECURSIVE CASE
❷ let head = numbers[0];
❸ let tail = numbers.slice(1, numbers.length);
❹ return head + sum(tail);
}
}
let nums = [1, 2, 3, 4, 5];
document.write('The sum of ' + nums + ' is ' + sum(nums) + "<br />");
nums = [5, 2, 4, 8];
document.write('The sum of ' + nums + ' is ' + sum(nums) + "<br />");
nums = [1, 10, 100, 1000];
document.write('The sum of ' + nums + ' is ' + sum(nums) + "<br />");
</script>
The output of these programs is shown here:
The sum of [1, 2, 3, 4, 5] is 15
The sum of [5, 2, 4, 8] is 19
The sum of [1, 10, 100, 1000] is 1111
When called with an empty array argument, the base case of our function simply returns 0 ❶. In the recursive case, we form the head ❷ and the tail ❸ from the original numbers argument. Keep in mind that the data type of tail is an array of numbers, just like the numbers argument. But the data type of head is just a single number value, and not an array with one number value. The return value of the sum() function is also a single number value and not an array of numbers; this is why we can add head and sum(tail) together in the recursive case ❹.
Each recursive call passes a smaller and smaller array to sum(), bringing it closer to the base case of an empty array. For example, Figure 3-1 shows the state of the call stack for sum([5, 2, 4, 8]).
In this figure, each card in the stack represents a function call. At the top of each card is the function name with the argument it was passed when called. Beneath that are the local variables: the numbers parameter, and the head and tail local variables created during the call. At the bottom of the card is the head + sum(tail) expression that the function call returns. When a new recursive function is made, a new card is pushed to the stack. When the function call returns, the top card is popped from the stack.
![A series of stacks of cards representing frame objects on the call stack. In order, the new top card represents a call to sum() passing [5, 2, 4, 8], then passing [2, 4, 8], then passing [4, 8], then passing [8], then passing an empty list. Then the top cards are removed, first removing the empty list card, then the [8] card, then [4, 8], then [2, 4, 8], then [5, 2, 4, 8].](images/000080.webp)
Figure 3-1: The state of the call stack when sum([5, 2, 4, 8]) runs
We can use the sum() function as a template for applying the head-tail technique to other recursive functions. For example, you can change the sum() function from one that sums an array of numbers to a concat() function that concatenates an array of strings together. The base case would return an empty string for an empty array argument, while the recursive case would return the head string joined with the return value of the recursive call that is passed the tail.
Recall from Chapter 2 that recursion is especially suited for problems that involve a tree-like structure and backtracking. An array, string, or other linear data structure can be considered a tree-like structure, albeit a tree that has only one branch at each node, as in Figure 3-2.
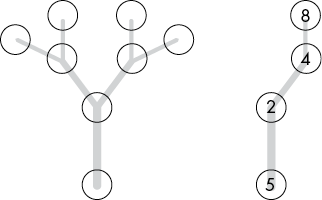
Figure 3-2: A [5, 2, 4, 8] array (right) is like a tree data structure (left) with only one branch at each node.
The key “tell” that our recursive function is unnecessary is that it never does any backtracking over the data it processes. It makes a single pass over each element in the array from beginning to end, which is something a basic loop can accomplish. Additionally, the Python recursive summation function is about 100 times slower than a straightforward iterative algorithm. Even if performance weren’t an issue, the recursive sum() function would cause a stack overflow if passed a list with tens of thousands of numbers to sum. Recursion is an advanced technique, but it isn’t always the best approach.
In Chapter 5, we’ll examine a recursive summation function that uses a divide-and-conquer strategy, and in Chapter 8 we’ll examine one that uses tail call optimization. These alternate recursive approaches work around some of the problems in the summation function in this chapter.
Like summing the numbers in an array, reversing a string is another frequently cited recursive algorithm even though the iterative solution is straightforward. Because a string is essentially an array of single characters, we’ll employ the head and tail approach for our rev() function just as we did for the summation algorithm.
Let’s start with the smallest strings possible. A blank string and a single-character string are already the reverse of themselves. These naturally form our base cases: if the string argument is a string such as '' or 'A', our function should simply return the string argument.
For larger strings, let’s try splitting the string into a head (just the first character) and tail (all characters after the first). For a two-character string like 'XY', 'X' is the head and 'Y' is the tail. To reverse the string, we need to place the head behind the tail: 'YX'.
Does this algorithm hold for longer strings? To reverse a string like 'CAT', we would break it into the head 'C' and the tail 'AT'. But placing the head behind the tail alone doesn’t reverse the string; it gives us 'ATC'. What we actually want to do is put the head behind the reverse of the tail. In other words, 'AT' would reverse to 'TA', and then adding the head to the end of that would produce the reversed string, 'TAC'.
How can we reverse the tail? Well, we can recursively call rev() and pass it the tail. Forget about the implementation of our function for a moment and focus on its input and output: rev() takes one string argument and returns a string with the argument’s characters reversed.
Thinking about how to implement a recursive function like rev() can be difficult because it involves a chicken-and-egg problem. In order to write rev()’s recursive case, we need to call a function that reverses a string—that is, rev(). As long as we have a solid understanding of what our recursive function’s arguments and return value will be, we can use the leap-of-faith technique to get around this chicken-and-egg problem by writing our recursive case assuming the rev() function call returns the correct value even though we haven’t finished writing it yet.
Taking a leap of faith in recursion is not a magical technique that guarantees your code works bug free. It is merely a perspective to hold to break past the mental programmer’s block you can have when thinking about how to implement your recursive function. The leap of faith requires you to have a firm understanding of your recursive function’s arguments and return value.
Note that the leap-of-faith technique only helps you write the recursive case. You must pass to the recursive call an argument that is closer to the base case. You can’t simply pass the same argument that the recursive function received, like this:
def rev(theString):
return rev(theString) # This won't magically work.
To continue our 'CAT' example, when we pass the tail 'AT' to rev(), the head is 'A' and the tail is 'T' in that function call. We already know that the reverse of a single-character string like 'T' is simply 'T'; that’s our base case. So this second call to rev() will reverse 'AT' to 'TA', which is precisely what the previous call to rev() needs. Figure 3-3 shows the state of the call stack during all the recursive calls to rev().
Let’s ask our three recursive algorithm questions about the rev() function:
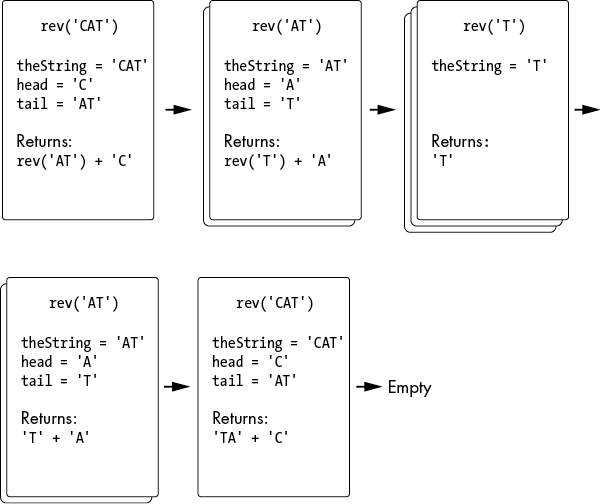
Figure 3-3: The state of the call stack as the rev() function reverses the CAT string
Here is reverseString.py, a Python program to reverse a string:
Python
def rev(theString):
❶ if len(theString) == 0 or len(theString) == 1:
# BASE CASE
return theString
else:
# RECURSIVE CASE
❷ head = theString[0]
❸ tail = theString[1:]
❹ return rev(tail) + head
print(rev('abcdef'))
print(rev('Hello, world!'))
print(rev(''))
print(rev('X'))
And here is the equivalent JavaScript code in reverseString.html:
JavaScript
<script type="text/javascript">
function rev(theString) {
❶ if (theString.length === 0 || theString.length === 1) {
// BASE CASE
return theString;
} else {
// RECURSIVE CASE
❷ let head = theString[0];
❸ let tail = theString.substring(1, theString.length);
❹ return rev(tail) + head;
}
}
document.write(rev("abcdef") + "<br />");
document.write(rev("Hello, world!") + "<br />");
document.write(rev("") + "<br />");
document.write(rev("X") + "<br />");
</script>
Here is the output of these programs:
fedcba
!dlrow ,olleH
X
Our recursive function rev() returns the string that is the reverse of the argument, theString. Let’s consider the simplest strings to reverse: the empty string and a single-character string would “reverse” to themselves. These are the two base cases with which we’ll start (though we combine them with an or or || Boolean operator ❶). For the recursive case, we form head from the first character in theString ❷, and tail from every character after the first ❸. The recursive case then returns the reverse of tail followed by the head character ❹.
A palindrome is a word or phrase that is spelled the same when written forward and backward. Level, race car, taco cat, and a man, a plan, a canal . . . Panama are all examples of palindromes. If you would like to detect whether a string is a palindrome, you can write a recursive isPalindrome() function.
The base case is a zero- or one-character string, which by its nature is always the same, whether forward or backward. We’ll use an approach similar to the head-tail technique, except that we’ll split the string argument into head, middle, and last strings instead. If the head and last characters are the same and the middle characters also form a palindrome, the string is a palindrome. The recursion comes from passing the middle string to isPalindrome().
Let’s ask the three recursive algorithm questions about the isPalindrome() function:
True because it is always a palindrome.Here is palindrome.py, a Python program to detect palindromes:
Python
def isPalindrome(theString):
if len(theString) == 0 or len(theString) == 1:
# BASE CASE
return True
else:
# RECURSIVE CASE
❶ head = theString[0]
❷ middle = theString[1:-1]
❸ last = theString[-1]
❹ return head == last and isPalindrome(middle)
text = 'racecar'
print(text + ' is a palindrome: ' + str(isPalindrome(text)))
text = 'amanaplanacanalpanama'
print(text + ' is a palindrome: ' + str(isPalindrome(text)))
text = 'tacocat'
print(text + ' is a palindrome: ' + str(isPalindrome(text)))
text = 'zophie'
print(text + ' is a palindrome: ' + str(isPalindrome(text)))
Here is the equivalent JavaScript code in palindrome.html:
JavaScript
<script type="text/javascript">
function isPalindrome(theString) {
if (theString.length === 0 || theString.length === 1) {
// BASE CASE
return true;
} else {
// RECURSIVE CASE
❶ let head = theString[0];
❷ let middle = theString.substring(1, theString.length -1);
❸ let last = theString[theString.length - 1];
❹ return head === last && isPalindrome(middle);
}
}
text = "racecar";
document.write(text + " is a palindrome: " + isPalindrome(text) + "<br />");
text = "amanaplanacanalpanama";
document.write(text + " is a palindrome: " + isPalindrome(text) + "<br />");
text = "tacocat";
document.write(text + " is a palindrome: " + isPalindrome(text) + "<br />");
text = "zophie";
document.write(text + " is a palindrome: " + isPalindrome(text) + "<br />");
</script>
Here is the output of these programs:
racecar is a palindrome: True
amanaplanacanalpanama is a palindrome: True
tacocat is a palindrome: True
zophie is a palindrome: False
The base case returns True because a zero- or one-character string is always a palindrome. Otherwise, the string argument is broken into three pieces: the first character ❶, the last character ❸, and the middle characters between them ❷.
The return statement in the recursive case ❹ makes use of Boolean short-circuiting, a feature of almost every programming language. In an expression joined with the and or && Boolean operators, if the left-side expression is False, it doesn’t matter if the right-side expression is True or False because the entire expression will be False. Boolean short-circuiting is an optimization that skips the evaluation of the right-side expression of an and operator if the left side is False. So, in the expression head == last and isPalindrome(middle), if head == last is False, the recursive call to isPalindrome() is skipped. This means that as soon as the head and last strings don’t match, the recursion stops and simply returns False.
This recursive algorithm is still sequential, like the summation and reverse-string functions in the previous sections, except that instead of going from the start of the data to the end, it goes from both ends of the data toward the middle. The iterative version of this algorithm that uses a simple loop is more straightforward. We cover the recursive version in this book because it’s a common coding interview problem.
The Tower of Hanoi is a puzzle involving a tower of stacked disks. The puzzle begins with the largest disk on the bottom, and the disk sizes decrease going up. Each disk has a hole in its center so that the disks can be stacked on top of one another on a pole. Figure 3-4 shows a wooden Tower of Hanoi puzzle.

Figure 3-4: A wooden Tower of Hanoi puzzle set
To solve the puzzle, the player must move the stack of disks from one pole to another while following three rules:
Python’s built-in turtledemo module has a Tower of Hanoi demonstration that you can see by running python -m turtledemo on Windows or python3 -m turtledemo on macOS/Linux, and then selecting minimum_hanoi from the Examples menu. Tower of Hanoi animations are readily found through an internet search as well.
The recursive algorithm for solving the Tower of Hanoi puzzle is not intuitive. Let’s start with the smallest case: a Tower of Hanoi with one disk. The solution is trivial: move the disk to another pole and you’re finished. Solving for two disks is slightly more complicated: move the smaller disk to one pole (we’ll call it the temporary pole) and the larger disk to the other pole (we’ll call it the end pole), and then finally move the smaller disk from the temporary pole to the end pole. Both disks are now on the end pole in the correct order.
Once you solve the three-disk tower, you’ll notice that a pattern emerges. To solve a tower of n disks from the start pole to the end pole, you must do the following:
Like the Fibonacci algorithm, the recursive case for the Tower of Hanoi algorithm makes two recursive calls instead of just one. If we draw a tree diagram of the operations for solving a four-disk Tower of Hanoi, it looks like Figure 3-5. Solving the four-disk puzzle requires the same steps as solving the three-disk puzzle, as well as moving the fourth disk and performing the steps of solving the three-disk puzzle again. Likewise, solving the three-disk puzzle requires the same steps as the two-disk puzzle plus moving the third disk, and so on. Solving the one-disk puzzle is the trivial base case: it involves only moving the disk.
The tree-like structure in Figure 3-5 hints that a recursive approach is ideal for solving the Tower of Hanoi puzzle. In this tree, the execution moves from top to bottom and from left to right.
While a three-disk or four-disk Tower of Hanoi is easy for a human to solve, increasing numbers of disks require an exponentially increasing number of operations to complete. For n disks, it takes a minimum of 2^n – 1 moves to solve. This means a 30-disk tower requires over a billion moves to complete!
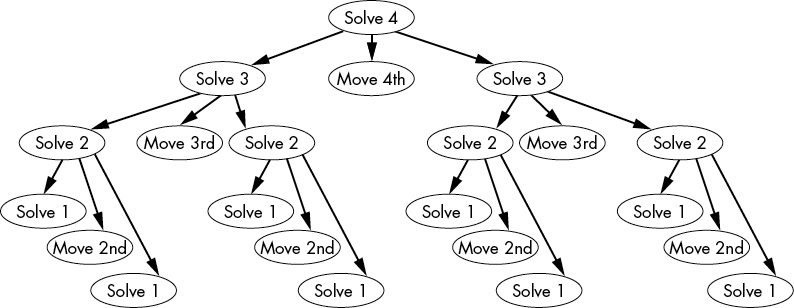
Figure 3-5: The series of operations for solving a four-disk Tower of Hanoi
Let’s ask ourselves the three questions for creating a recursive solution:
The following towerOfHanoiSolver.py program solves the Tower of Hanoi puzzle and displays a visualization of each step:
import sys
# Set up towers A, B, and C. The end of the list is the top of the tower.
TOTAL_DISKS = 6 ❶
# Populate Tower A:
TOWERS = {'A': list(reversed(range(1, TOTAL_DISKS + 1))), ❷
'B': [],
'C': []}
def printDisk(diskNum):
# Print a single disk of width diskNum.
emptySpace = ' ' * (TOTAL_DISKS - diskNum)
if diskNum == 0:
# Just draw the pole.
sys.stdout.write(emptySpace + '||' + emptySpace)
else:
# Draw the disk.
diskSpace = '@' * diskNum
diskNumLabel = str(diskNum).rjust(2, '_')
sys.stdout.write(emptySpace + diskSpace + diskNumLabel + diskSpace + emptySpace)
def printTowers():
# Print all three towers.
for level in range(TOTAL_DISKS, -1, -1):
for tower in (TOWERS['A'], TOWERS['B'], TOWERS['C']):
if level >= len(tower):
printDisk(0)
else:
printDisk(tower[level])
sys.stdout.write('\n')
# Print the tower labels A, B, and C.
emptySpace = ' ' * (TOTAL_DISKS)
print('%s A%s%s B%s%s C\n' % (emptySpace, emptySpace, emptySpace, emptySpace, emptySpace))
def moveOneDisk(startTower, endTower):
# Move the top disk from startTower to endTower.
disk = TOWERS[startTower].pop()
TOWERS[endTower].append(disk)
def solve(numberOfDisks, startTower, endTower, tempTower):
# Move the top numberOfDisks disks from startTower to endTower.
if numberOfDisks == 1:
# BASE CASE
moveOneDisk(startTower, endTower) ❸
printTowers()
return
else:
# RECURSIVE CASE
solve(numberOfDisks - 1, startTower, tempTower, endTower) ❹
moveOneDisk(startTower, endTower) ❺
printTowers()
solve(numberOfDisks - 1, tempTower, endTower, startTower) ❻
return
# Solve:
printTowers()
solve(TOTAL_DISKS, 'A', 'B', 'C')
# Uncomment to enable interactive mode:
#while True:
# printTowers()
# print('Enter letter of start tower and the end tower. (A, B, C) Or Q to quit.')
# move = input().upper()
# if move == 'Q':
# sys.exit()
# elif move[0] in 'ABC' and move[1] in 'ABC' and move[0] != move[1]:
# moveOneDisk(move[0], move[1])
This towerOfHanoiSolver.html program contains the equivalent JavaScript code:
<script type="text/javascript">
// Set up towers A, B, and C. The end of the array is the top of the tower.
let TOTAL_DISKS = 6; ❶
let TOWERS = {"A": [], ❷
"B": [],
"C": []};
// Populate Tower A:
for (let i = TOTAL_DISKS; i > 0; i--) {
TOWERS["A"].push(i);
}
function printDisk(diskNum) {
// Print a single disk of width diskNum.
let emptySpace = " ".repeat(TOTAL_DISKS - diskNum);
if (diskNum === 0) {
// Just draw the pole.
document.write(emptySpace + "||" + emptySpace);
} else {
// Draw the disk.
let diskSpace = "@".repeat(diskNum);
let diskNumLabel = String("___" + diskNum).slice(-2);
document.write(emptySpace + diskSpace + diskNumLabel + diskSpace + emptySpace);
}
}
function printTowers() {
// Print all three towers.
let towerLetters = "ABC";
for (let level = TOTAL_DISKS; level >= 0; level--) {
for (let towerLetterIndex = 0; towerLetterIndex < 3; towerLetterIndex++) {
let tower = TOWERS[towerLetters[towerLetterIndex]];
if (level >= tower.length) {
printDisk(0);
} else {
printDisk(tower[level]);
}
}
document.write("<br />");
}
// Print the tower labels A, B, and C.
let emptySpace = " ".repeat(TOTAL_DISKS);
document.write(emptySpace + " A" + emptySpace + emptySpace +
" B" + emptySpace + emptySpace + " C<br /><br />");
}
function moveOneDisk(startTower, endTower) {
// Move the top disk from startTower to endTower.
let disk = TOWERS[startTower].pop();
TOWERS[endTower].push(disk);
}
function solve(numberOfDisks, startTower, endTower, tempTower) {
// Move the top numberOfDisks disks from startTower to endTower.
if (numberOfDisks == 1) {
// BASE CASE
moveOneDisk(startTower, endTower); ❸
printTowers();
return;
} else {
// RECURSIVE CASE
solve(numberOfDisks - 1, startTower, tempTower, endTower); ❹
moveOneDisk(startTower, endTower); ❺
printTowers();
solve(numberOfDisks - 1, tempTower, endTower, startTower); ❻
return;
}
}
// Solve:
document.write("<pre>");
printTowers();
solve(TOTAL_DISKS, "A", "B", "C");
document.write("</pre>");
</script>
When you run this code, the output shows each move of the disks until the entire tower has moved from Tower A to Tower B:
|| || ||
@_1@ || ||
@@_2@@ || ||
@@@_3@@@ || ||
@@@@_4@@@@ || ||
@@@@@_5@@@@@ || ||
@@@@@@_6@@@@@@ || ||
A B C
|| || ||
|| || ||
@@_2@@ || ||
@@@_3@@@ || ||
@@@@_4@@@@ || ||
@@@@@_5@@@@@ || ||
@@@@@@_6@@@@@@ || @_1@
A B C
--snip--
|| || ||
|| || ||
|| || ||
|| || ||
|| @@_2@@ ||
@_1@ @@@_3@@@ ||
@@@@@@_6@@@@@@ @@@@_4@@@@ @@@@@_5@@@@@
--snip--
A B C
|| || ||
|| @_1@ ||
|| @@_2@@ ||
|| @@@_3@@@ ||
|| @@@@_4@@@@ ||
|| @@@@@_5@@@@@ ||
|| @@@@@@_6@@@@@@ ||
A B C
The Python version has an interactive mode too, where you can solve the puzzle yourself. Uncomment the lines of code at the end of towerOfHanoiSolver.py to play the interactive version.
You can start by running the program with the smaller cases by setting the TOTAL_DISKS constant ❶ at the top of the program to 1 or 2. In our program, a list of integers in Python and an array of integers in JavaScript represent a pole. The integer represents a disk, with larger integers representing larger disks. The integer at the start of the list or array is at the bottom of the pole, and the integer at the end is at the pole’s top. For example, [6, 5, 4, 3, 2, 1] represents the starting pole with six disks with the largest on the bottom, while [] represents a pole with no disks. The TOWERS variable contains three of these lists ❷.
The base case merely moves the smallest disk from the start pole to the end pole ❸. The recursive case for a tower of n disks carries out three steps: solving the n – 1 case ❹, moving the nth disk ❺, and then solving the n – 1 case again ❻.
Graphics programs commonly use the flood fill algorithm to fill an arbitrarily shaped area of the same color with another color. Figure 3-6 shows one such shape at the top left. The subsequent panels show three different sections of the shape flood-filled with a gray color. The flood fill begins on a white pixel and spreads until it meets a non-white pixel, filling the enclosed space.
The flood fill algorithm is recursive: it begins by changing a single pixel to a new color. The recursive function is then called on any neighbors of the pixel with its same old color. It then moves on to the neighbors of the neighbors, and so on, converting each pixel to the new color until the enclosed space is filled in.
The base case is a pixel whose color is the edge of the image or is not the old color. Since reaching the base case is the only way to stop the “spread” of recursive calls for every pixel in the image, this algorithm has the emergent behavior of changing all the contiguous pixels from the old color to the new color.
Let’s ask the three recursive algorithm questions about our floodFill() function:
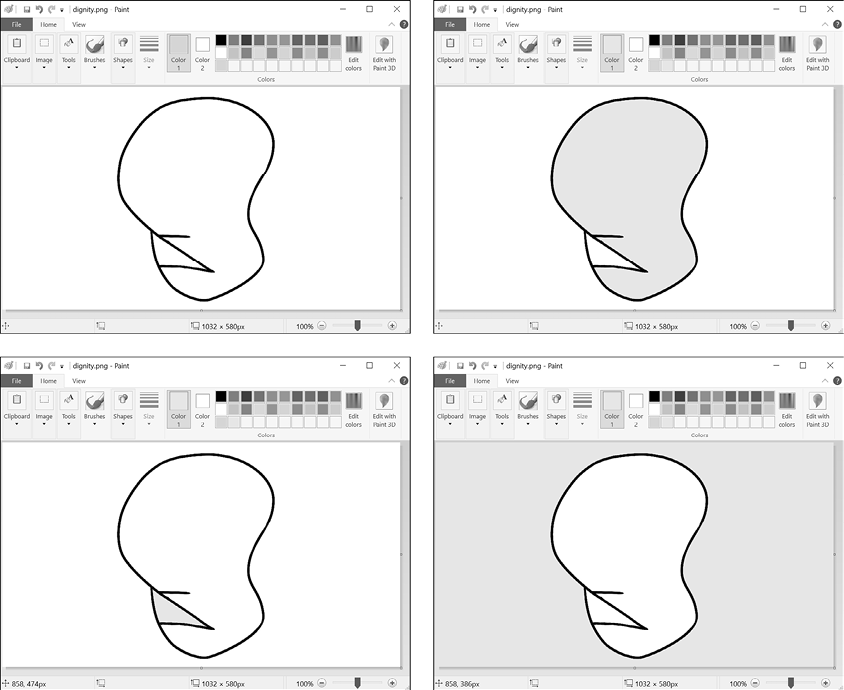
Figure 3-6: The original shape in a graphics editor (top left) and the same shape with three different areas flood-filled with a light gray color
Instead of an image for our sample program, we’ll use a list of single-character strings to form a 2D grid of text characters to represent an “image.” Each string represents a “pixel,” and the specific character represents the “color.” The floodfill.py Python program implements the flood fill algorithm, the image data, and a function to print the image on the screen:
Python
import sys
# Create the image (make sure it's rectangular!)
❶ im = [list('..########################...........'),
list('..#......................#...#####...'),
list('..#..........########....#####...#...'),
list('..#..........#......#............#...'),
list('..#..........########.........####...'),
list('..######......................#......'),
list('.......#..#####.....###########......'),
list('.......####...#######................')]
HEIGHT = len(im)
WIDTH = len(im[0])
def floodFill(image, x, y, newChar, oldChar=None):
if oldChar == None:
# oldChar defaults to the character at x, y.
❷ oldChar = image[y][x]
if oldChar == newChar or image[y][x] != oldChar:
# BASE CASE
return
image[y][x] = newChar # Change the character.
# Uncomment to view each step:
#printImage(image)
# Change the neighboring characters.
if y + 1 < HEIGHT and image[y + 1][x] == oldChar:
# RECURSIVE CASE
❸ floodFill(image, x, y + 1, newChar, oldChar)
if y - 1 >= 0 and image[y - 1][x] == oldChar:
# RECURSIVE CASE
❹ floodFill(image, x, y - 1, newChar, oldChar)
if x + 1 < WIDTH and image[y][x + 1] == oldChar:
# RECURSIVE CASE
❺ floodFill(image, x + 1, y, newChar, oldChar)
if x - 1 >= 0 and image[y][x - 1] == oldChar:
# RECURSIVE CASE
❻ floodFill(image, x - 1, y, newChar, oldChar)
❼ return # BASE CASE
def printImage(image):
for y in range(HEIGHT):
# Print each row.
for x in range(WIDTH):
# Print each column.
sys.stdout.write(image[y][x])
sys.stdout.write('\n')
sys.stdout.write('\n')
printImage(im)
floodFill(im, 3, 3, 'o')
printImage(im)
The floodfill.html program contains the equivalent JavaScript code:
JavaScript
<script type="text/javascript">
// Create the image (make sure it's rectangular!)
❶ let im = ["..########################...........".split(""),
"..#......................#...#####...".split(""),
"..#..........########....#####...#...".split(""),
"..#..........#......#............#...".split(""),
"..#..........########.........####...".split(""),
"..######......................#......".split(""),
".......#..#####.....###########......".split(""),
".......####...#######................".split("")];
let HEIGHT = im.length;
let WIDTH = im[0].length;
function floodFill(image, x, y, newChar, oldChar) {
if (oldChar === undefined) {
// oldChar defaults to the character at x, y.
❷ oldChar = image[y][x];
}
if ((oldChar == newChar) || (image[y][x] != oldChar)) {
// BASE CASE
return;
}
image[y][x] = newChar; // Change the character.
// Uncomment to view each step:
//printImage(image);
// Change the neighboring characters.
if ((y + 1 < HEIGHT) && (image[y + 1][x] == oldChar)) {
// RECURSIVE CASE
❸ floodFill(image, x, y + 1, newChar, oldChar);
}
if ((y - 1 >= 0) && (image[y - 1][x] == oldChar)) {
// RECURSIVE CASE
❹ floodFill(image, x, y - 1, newChar, oldChar);
}
if ((x + 1 < WIDTH) && (image[y][x + 1] == oldChar)) {
// RECURSIVE CASE
❺ floodFill(image, x + 1, y, newChar, oldChar);
}
if ((x - 1 >= 0) && (image[y][x - 1] == oldChar)) {
// RECURSIVE CASE
❻ floodFill(image, x - 1, y, newChar, oldChar);
}
❼ return; // BASE CASE
}
function printImage(image) {
document.write("<pre>");
for (let y = 0; y < HEIGHT; y++) {
// Print each row.
for (let x = 0; x < WIDTH; x++) {
// Print each column.
document.write(image[y][x]);
}
document.write("\n");
}
document.write("\n</pre>");
}
printImage(im);
floodFill(im, 3, 3, "o");
printImage(im);
</script>
When you run this code, the program fills the interior of the shape drawn by the # characters ❶ starting at coordinates 3, 3. It replaces all the period characters (.) with o characters. The following output shows the before and after images:
..########################...........
..#......................#...#####...
..#..........########....#####...#...
..#..........#......#............#...
..#..........########.........####...
..######......................#......
.......#..#####.....###########......
.......####...#######................
..########################...........
..#oooooooooooooooooooooo#...#####...
..#oooooooooo########oooo#####ooo#...
..#oooooooooo#......#oooooooooooo#...
..#oooooooooo########ooooooooo####...
..######oooooooooooooooooooooo#......
.......#oo#####ooooo###########......
.......####...#######................
If you want to see every step of the flood fill algorithm as it fills in the new character, uncomment the printImage(image) line in the floodFill() function and run the program again.
The image is represented by a 2D array of string characters. We can pass this image data structure, an x coordinate and a y coordinate, and a new character to the floodFill() function. The function notes the character currently at the x and y coordinates and saves it to the oldChar variable ❷.
If the current characters at coordinates x and y in image are not the same as oldChar, this is our base case, and the function simply returns. Otherwise, the function continues on to its four recursive cases: passing the x- and y-coordinates of the bottom ❸, top ❹, right ❺, and left ❻ neighbors of the current coordinates. After these four potential recursive calls are made, the end of the function is an implicit base case, made explicit in our program with a return statement ❼.
The flood fill algorithm doesn’t have to be recursive. For large images, a recursive function could cause stack overflows. If we were to implement flood fill with a loop and a stack instead, the stack would begin with the x- and y-coordinates of the starting pixel. The code in the loop would pop the coordinates off the top of the stack, and if that coordinate’s pixel matches oldChar, it would push the coordinates of the four neighboring pixels. When the stack is empty because the base case is no longer pushing neighbors to the stack, the loop is finished.
However, the flood fill algorithm doesn’t necessarily have to use a stack. The pushing and popping of a first-in, last-out stack is effective for backtracking behavior, but the order that the pixels are processed in the flood fill algorithm can be arbitrary. This means we could equally effectively use a set data structure that removes elements randomly. You can find these iterative flood fill algorithms implemented in floodFillIterative.py and floodFillIterative.html in the downloadable resources at https://nostarch.com/recursive-book-recursion.
The Ackermann function is named after its discoverer, Wilhelm Ackermann. A student of mathematician David Hilbert (whose Hilbert curve fractal we discuss in Chapter 9), Ackermann published his function in 1928. Mathematicians Rózsa Péter and Raphael Robinson later developed the version of the function featured in this section.
While the Ackermann function has some application in advanced mathematics, it is mostly known for being an example of a highly recursive function. Even slight increases to its two integer arguments cause a large increase in the number of recursive calls it makes.
The Ackermann function takes two arguments, m and n, and has a base case of returning n + 1 when m is 0. There are two recursive cases: when n is 0, the function returns ackermann(m - 1, 1), and when n is greater than 0, the function returns ackermann(m - 1, ackermann(m, n - 1)). These cases likely aren’t meaningful to you, but suffice it to say, the number of recursive calls the Ackermann function makes grows quickly. Calling ackermann(1, 1) results in three recursive function calls. Calling ackermann(2, 3) results in 43 recursive function calls. Calling ackermann(3, 5) results in 42,437 recursive function calls. And calling ackermann(5, 7) results in . . . well, actually I don’t know how many recursive function calls, because it would take several times the age of the universe to calculate.
Let’s answer the three questions we ask when constructing recursive algorithms:
m is 0.m or m - 1 is passed for the next m parameter; and 1, n - 1, or the return value of ackermann(m, n - 1) is passed for the next n parameter.m argument is always either decreasing or staying the same size, so it will eventually reach 0.Here is an ackermann.py Python program:
def ackermann(m, n, indentation=None):
if indentation is None:
indentation = 0
print('%sackermann(%s, %s)' % (' ' * indentation, m, n))
if m == 0:
# BASE CASE
return n + 1
elif m > 0 and n == 0:
# RECURSIVE CASE
return ackermann(m - 1, 1, indentation + 1)
elif m > 0 and n > 0:
# RECURSIVE CASE
return ackermann(m - 1, ackermann(m, n - 1, indentation + 1), indentation + 1)
print('Starting with m = 1, n = 1:')
print(ackermann(1, 1))
print('Starting with m = 2, n = 3:')
print(ackermann(2, 3))
And here is the equivalent ackermann.html JavaScript program:
<script type="text/javascript">
function ackermann(m, n, indentation) {
if (indentation === undefined) {
indentation = 0;
}
document.write(" ".repeat(indentation) + "ackermann(" + m + ", " + n + ")\n");
if (m === 0) {
// BASE CASE
return n + 1;
} else if ((m > 0) && (n === 0)) {
// RECURSIVE CASE
return ackermann(m - 1, 1, indentation + 1);
} else if ((m > 0) && (n > 0)) {
// RECURSIVE CASE
return ackermann(m - 1, ackermann(m, n - 1, indentation + 1), indentation + 1);
}
}
document.write("<pre>");
document.write("Starting with m = 1, n = 1:<br />");
document.write(ackermann(1, 1) + "<br />");
document.write("Starting with m = 2, n = 3:<br />");
document.write(ackermann(2, 3) + "<br />");
document.write("</pre>");
</script>
When you run this code, the output’s indentation (set by the indentation argument) tells you how deep on the call stack the given recursive function call is:
Starting with m = 1, n = 1:
ackermann(1, 1)
ackermann(1, 0)
ackermann(0, 1)
ackermann(0, 2)
3
Starting with m = 2, n = 3:
ackermann(2, 3)
ackermann(2, 2)
ackermann(2, 1)
ackermann(2, 0)
--snip--
ackermann(0, 6)
ackermann(0, 7)
ackermann(0, 8)
9
You can also try ackermann(3, 3), but anything with larger arguments will probably take far too long to calculate. To speed up the calculation, try commenting out all print() and document.write() calls except the ones that print the final return value of ackermann().
Remember, even a recursive algorithm like the Ackermann function can be implemented as an iterative function. The iterative Ackermann algorithms are implemented in ackermannIterative.py and ackermannIterative.html in the downloadable resources at https://nostarch.com/recursive-book-recursion.
This chapter covered some classic recursive algorithms. For each, we asked the three important questions you should always ask when designing your own recursive functions: What is the base case? What arguments are passed to the recursive function call? How do these arguments become closer to the base case? If they don’t, your function will continue to recurse until it causes a stack overflow.
The summation, string reversing, and palindrome detection recursive functions could have easily been implemented with a simple loop. The key giveaway is that they all make a single pass through the data given to them with no backtracking. As explained in Chapter 2, recursive algorithms are especially suited to problems that involve a tree-like structure and require backtracking.
The tree-like structures for solving the Tower of Hanoi puzzle suggest that it involves backtracking, as the program execution runs from top to bottom, left to right, in the tree. This makes it a prime candidate for recursion, especially since the solution requires two recursive calls of smaller towers.
The flood fill algorithm is directly applicable to graphics and drawing programs, as well as other algorithms to detect the shape of contiguous areas. If you’ve used the paint-bucket tool in a graphics program, you’ve likely used a version of the flood fill algorithm.
The Ackermann function is an excellent example of how quickly a recursive function can grow as its inputs increase. While it doesn’t have many practical applications in day-to-day programming, no discussion about recursion would be complete without it. But as recursive as it is, like all recursive functions it can be implemented iteratively with a loop and a stack.
Wikipedia has more information on the Tower of Hanoi problem at https://en.wikipedia.org/wiki/Tower_of_Hanoi, and the Computerphile video “Recursion ‘Super Power’ (in Python)” covers solving the Tower of Hanoi in Python at https://youtu.be/8lhxIOAfDss. The 3Blue1Brown two-part video series, “Binary, Hanoi, and Sierpiński,” goes into even more detail by exploring the relationships among the Tower of Hanoi, binary numbers, and the Sierpiński Triangle fractal starting at https://youtu.be/2SUvWfNJSsM.
Wikipedia has an animation of the flood fill algorithm working on a small image at https://en.wikipedia.org/wiki/Flood_fill.
The Computerphile video “The Most Difficult Program to Compute?” discusses the Ackermann function at https://youtu.be/i7sm9dzFtEI. If you’d like to learn more about the Ackermann function’s place in computability theory, the Hackers in Cambridge channel has a five-part video series on primitive recursive and partial recursive functions at https://youtu.be/yaDQrOUK-KY. The series requires a lot of mathematical thinking on the part of the viewer, but you don’t need a lot of prior mathematical knowledge.
Test your comprehension by answering the following questions:
sum() function involve any backtracking over the data it works on?im variable’s strings to create a C shape that is not fully enclosed. What happens when you attempt to flood-fill the image from the middle of the C?Then re-create the recursive algorithms from this chapter without looking at the original code.
For practice, write a function for each of the following tasks:
concat() function that is passed an array of strings and returns these strings concatenated together into a single string. For example, concat(['Hello', 'World']) should return HelloWorld.product() function that is passed an array of integers and returns the total multiplied product of them. This code will be almost identical to the sum() function in this chapter. However, note that the base case of an array with just one integer returns the integer, and the base case of an empty array returns 1.for loops that call the flood fill function on each character in the grid if it is a period, in order to change the periods into hash characters. For example, the following data would result in the program finding six places in the grid with periods, meaning there are five rooms (and the space outside all the rooms).
...##########....................................
...#........#....####..................##########
...#........#....#..#...############...#........#
...##########....#..#...#..........#...##.......#
.......#....#....####...#..........#....##......#
.......#....#....#......############.....##.....#
.......######....#........................##....#
.................####........####..........######