Check out other books by Al Sweigart, free online or available for purchase:




...and other books as well! Or register for the online video course. You can also donate to support the author directly.





In previous chapters, you learned that recursion is especially suited for problems that involve a tree-like structure and backtracking, such as maze-solving algorithms. To see why, consider that a tree’s trunk splits off into multiple branches. Those branches themselves split off into other branches. In other words, a tree has a recursive, self-similar shape.
A maze can be represented by a tree data structure, since mazes branch off into different paths, which in turn branch off into more paths. When you reach a dead end in a maze, you must backtrack to an earlier branching point.
The task of traversing tree graphs is tightly linked with many recursive algorithms, such as the maze-solving algorithm in this chapter and the maze-generation program in Chapter 11. We’ll take a look at tree traversal algorithms and employ them to find certain names in a tree data structure. We’ll also use tree traversal for an algorithm to obtain the deepest node in a tree. Finally, we’ll see how mazes can be represented as a tree data structure, and employ tree traversal and backtracking to find a path from the start of the maze to the exit.
If you program in Python and JavaScript, you’re used to working with list, array, and dictionary data structures. You’ll encounter tree data structures only if you are dealing with low-level details of certain computer science algorithms such as abstract syntax trees, priority queues, Adelson-Velsky-Landis (AVL) trees, and other concepts beyond the scope of this book. However, trees themselves are simple enough concepts.
A tree data structure is a data structure composed of nodes that are connected to other nodes by edges. The nodes contain data, while the edges represent a relationship with another node. Nodes are also called vertices. The starting node of a tree is called the root, and the nodes at the end are called leaves. Trees always have exactly one root.
Parent nodes at the top have edges to zero or more child nodes beneath them. Therefore, leaves are the nodes that do not have children, parent nodes are the non-leaf nodes, and child nodes are all the non-root nodes. Nodes in a tree can have edges to multiple child nodes. The parent nodes that connect a child node to the root node are also called the child node’s ancestors. The child nodes between a parent node and a leaf node are called the parent node’s descendants. Parent nodes in a tree can have multiple child nodes. But every child node has exactly one parent, except for the root node, which has zero parents. In trees, only one path can exist between any two nodes.
Figure 4-1 shows an example of a tree and three examples of structures that are not trees.
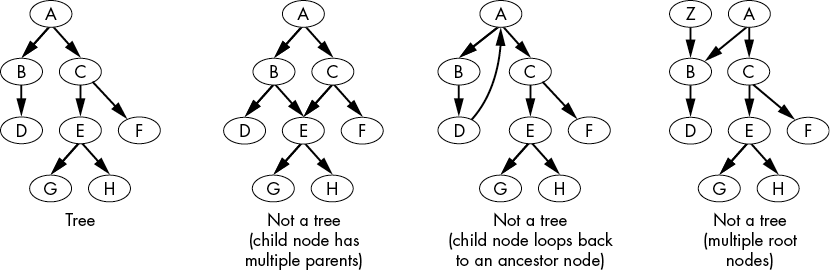
Figure 4-1: A tree (left) and three examples of non-trees
As you can see, child nodes must have one parent and not have an edge that creates a loop, or else the structure is no longer considered a tree. The recursive algorithms we cover in this chapter apply only to tree data structures.
Tree data structures are often drawn growing downward, with the root at the top. Figure 4-2 shows a tree created with the following Python code (it’s also valid JavaScript code):
root = {'data': 'A', 'children': []}
node2 = {'data': 'B', 'children': []}
node3 = {'data': 'C', 'children': []}
node4 = {'data': 'D', 'children': []}
node5 = {'data': 'E', 'children': []}
node6 = {'data': 'F', 'children': []}
node7 = {'data': 'G', 'children': []}
node8 = {'data': 'H', 'children': []}
root['children'] = [node2, node3]
node2['children'] = [node4]
node3['children'] = [node5, node6]
node5['children'] = [node7, node8]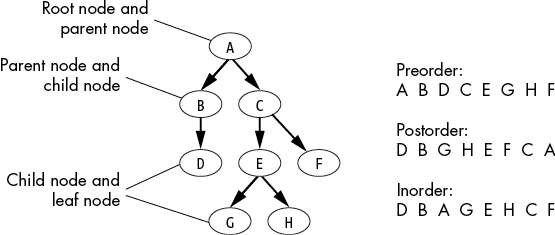
Figure 4-2: A tree with root A and leaves D, G, H, and F, along with its traversal orders
Each node in the tree contains a piece of data (a string of a letter from A to H) and a list of its child nodes. The preorder, postorder, and inorder information in Figure 4-2 is explained in subsequent sections.
In the code for this tree, each node is represented by a Python dictionary (or JavaScript object) with a key data that stores the node’s data, and a key children that has a list of other nodes. I use the root and node2 to node8 variables to store each node and make the code more readable, but they aren’t required. The following Python/JavaScript code is equivalent to the previous code listing, though harder for humans to read:
root = {'data': 'A', 'children': [{'data': 'B', 'children':
[{'data': 'D', 'children': []}]}, {'data': 'C', 'children':
[{'data': 'E', 'children': [{'data': 'G', 'children': []},
{'data': 'H', 'children': []}]}, {'data': 'F', 'children': []}]}]}The tree in Figure 4-2 is a specific kind of data structure called a directed acyclic graph (DAG). In mathematics and computer science, a graph is a collection of nodes and edges, and a tree is a kind of graph. The graph is directed because its edges have one direction: from parent to child node. Edges in a DAG are not undirected—that is, bidirectional. (Graphs in general do not have this restriction and can have edges in both directions, including from a child node back to its parent node.) The graph is acyclic because there are no loops, or cycles, from child nodes to their own ancestor nodes; the “branches” of the tree must keep growing in the same direction.
You can think of lists, arrays, and strings as linear trees; the root is the first element, and the nodes have only one child node. This linear tree terminates at its one leaf node. These linear trees are called linked lists, as each node has only one “next” node until the end of the list. Figure 4-3 shows a linked list that stores the characters in the word HELLO.
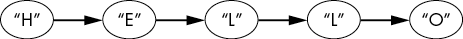
Figure 4-3: A linked list data structure storing HELLO. Linked lists can be considered a kind of tree data structure.
We’ll use the code for the tree in Figure 4-2 for this chapter’s examples. A tree traversal algorithm will visit each of the nodes in a tree by following the edges, starting from a root node.
We can write code to access data in any node by starting from the root node in root. For example, after entering the tree code into the Python or JavaScript interactive shell, run the following:
>>> root['children'][1]['data']
'C'
>>> root['children'][1]['children'][0]['data']
'E'Our tree traversal code can be written as a recursive function because tree data structures have a self-similar structure: a parent node has child nodes, and each child node is the parent node of its own children. Tree traversal algorithms ensure that your programs can access or modify the data in every node in the tree no matter its shape or size.
Let’s ask the three questions about recursive algorithms for our tree traversal code:
Keep in mind that tree data structures that are especially deep will cause a stack overflow as the algorithm traverses the deeper nodes. This happens because each level deeper into the tree requires yet another function call, and too many function calls without returning cause stack overflows. However, it’s unlikely for broad, well-balanced trees to be that deep. If every node in a 1,000 level deep tree has two children, the tree would have about 21000 nodes. That’s more atoms than there are in the universe, and it’s unlikely your tree data structure is that big.
Trees have three kinds of tree traversal algorithms: preorder, postorder, and inorder. We’ll discuss each of these in the next three sections.
Preorder tree traversal algorithms access a node’s data before traversing its child nodes. Use a preorder traversal if your algorithm needs to access the data in parent nodes before the data in their child nodes. For example, preorder traversals are used when you are creating a copy of the tree data structure, as you need to create the parent nodes before child nodes in the duplicate tree.
The following preorderTraversal.py program has a preorderTraverse() function that accesses the node’s data to print it to the screen first, before traversing each child node:
Python
root = {'data': 'A', 'children': [{'data': 'B', 'children':
[{'data': 'D', 'children': []}]}, {'data': 'C', 'children':
[{'data': 'E', 'children': [{'data': 'G', 'children': []},
{'data': 'H', 'children': []}]}, {'data': 'F', 'children': []}]}]}
def preorderTraverse(node):
print(node['data'], end=' ') # Access this node's data.
❶ if len(node['children']) > 0:
# RECURSIVE CASE
for child in node['children']:
preorderTraverse(child) # Traverse child nodes.
# BASE CASE
❷ return
preorderTraverse(root)The equivalent JavaScript program is in preorderTraversal.html:
JavaScript
<script type="text/javascript">
root = {"data": "A", "children": [{"data": "B", "children":
[{"data": "D", "children": []}]}, {"data": "C", "children":
[{"data": "E", "children": [{"data": "G", "children": []},
{"data": "H", "children": []}]}, {"data": "F", "children": []}]}]};
function preorderTraverse(node) {
document.write(node["data"] + " "); // Access this node's data.
❶ if (node["children"].length > 0) {
// RECURSIVE CASE
for (let i = 0; i < node["children"].length; i++) {
preorderTraverse(node["children"][i]); // Traverse child nodes.
}
}
// BASE CASE
❷ return;
}
preorderTraverse(root);
</script>The output of these programs is the node data in preorder order:
A B D C E G H FWhen you look at the tree in Figure 4-1, notice that preorder traversal order displays the data in left nodes before right nodes, and bottom nodes before top nodes.
All tree traversals begin by passing the root node to the recursive function. The function makes a recursive call and passes each of the root node’s children as the argument. Since these child nodes have children of their own, the traversal continues until a leaf node with no children is reached. At this point, the function call simply returns.
The recursive case occurs if the node has any child nodes ❶, in which case a recursive call is made with each of the children as the node argument. Whether or not the node has children, the base case always happens at the end of the function when it returns ❷.
Postorder tree traversal traverses a node’s child nodes before accessing the node’s data. For example, this traversal is used when deleting a tree and ensuring that no child nodes are “orphaned” by deleting their parent nodes first, leaving the child node inaccessible to the root node. The code in the following postorderTraversal.py program is similar to the preorder traversal code in the previous section, except the recursive function call comes before the print() call:
Python
root = {'data': 'A', 'children': [{'data': 'B', 'children':
[{'data': 'D', 'children': []}]}, {'data': 'C', 'children':
[{'data': 'E', 'children': [{'data': 'G', 'children': []},
{'data': 'H', 'children': []}]}, {'data': 'F', 'children': []}]}]}
def postorderTraverse(node):
for child in node['children']:
# RECURSIVE CASE
postorderTraverse(child) # Traverse child nodes.
print(node['data'], end=' ') # Access this node's data.
# BASE CASE
return
postorderTraverse(root)The postorderTraversal.html program has the equivalent JavaScript code:
JavaScript
<script type="text/javascript">
root = {"data": "A", "children": [{"data": "B", "children":
[{"data": "D", "children": []}]}, {"data": "C", "children":
[{"data": "E", "children": [{"data": "G", "children": []},
{"data": "H", "children": []}]}, {"data": "F", "children": []}]}]};
function postorderTraverse(node) {
for (let i = 0; i < node["children"].length; i++) {
// RECURSIVE CASE
postorderTraverse(node["children"][i]); // Traverse child nodes.
}
document.write(node["data"] + " "); // Access this node's data.
// BASE CASE
return;
}
postorderTraverse(root);
</script>The output of these programs is the node data in postorder order:
D B G H E F C AThe postorder traversal order of the nodes displays the data in left nodes before right nodes, and in bottom nodes before top nodes. When we compare the postorderTraverse() and preorderTraverse() functions, we find that the names are a bit of a misnomer: pre and post don’t refer to the order in which nodes are visited. The nodes are always traversed in the same order; we go down the child nodes first (called a depth-first search) as opposed to visiting the nodes in each level before going deeper (called a breadth-first search). The pre and post refer to when the node’s data is accessed: either before or after traversing the node’s children.
Binary trees are tree data structures with at most two child nodes, often called the left child and right child. An inorder tree traversal traverses the left child node, then accesses the node’s data, and then traverses the right child node. This traversal is used in algorithms that deal with binary search trees (which are beyond the scope of this book). The inorderTraversal.py program contains Python code that performs this kind of traversal:
Python
root = {'data': 'A', 'children': [{'data': 'B', 'children':
[{'data': 'D', 'children': []}]}, {'data': 'C', 'children':
[{'data': 'E', 'children': [{'data': 'G', 'children': []},
{'data': 'H', 'children': []}]}, {'data': 'F', 'children': []}]}]}
def inorderTraverse(node):
if len(node['children']) >= 1:
# RECURSIVE CASE
inorderTraverse(node['children'][0]) # Traverse the left child.
print(node['data'], end=' ') # Access this node's data.
if len(node['children']) >= 2:
# RECURSIVE CASE
inorderTraverse(node['children'][1]) # Traverse the right child.
# BASE CASE
return
inorderTraverse(root)The inorderTraversal.html program contains the equivalent JavaScript code:
JavaScript
<script type="text/javascript">
root = {"data": "A", "children": [{"data": "B", "children":
[{"data": "D", "children": []}]}, {"data": "C", "children":
[{"data": "E", "children": [{"data": "G", "children": []},
{"data": "H", "children": []}]}, {"data": "F", "children": []}]}]};
function inorderTraverse(node) {
if (node["children"].length >= 1) {
// RECURSIVE CASE
inorderTraverse(node["children"][0]); // Traverse the left child.
}
document.write(node["data"] + " "); // Access this node's data.
if (node["children"].length >= 2) {
// RECURSIVE CASE
inorderTraverse(node["children"][1]); // Traverse the right child.
}
// BASE CASE
return;
}
inorderTraverse(root);
</script>The output of these programs looks like this:
D B A G E H C FInorder traversal typically refers to the traversal of binary trees, although processing a node’s data after traversing the first node and before traversing the last node would count as inorder traversal for trees of any size.
Instead of printing out the data in each node as we traverse them, we can use a depth-first search to find specific data in a tree data structure. We’ll write an algorithm that searches the tree in Figure 4-4 for names that are exactly eight letters long. This is a rather contrived example, but it shows how an algorithm can use tree traversal to retrieve data out of a tree data structure.
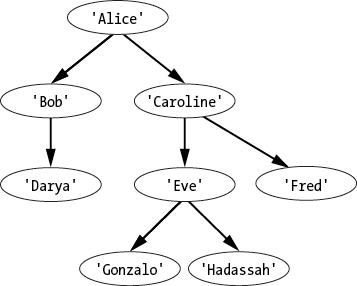
Figure 4-4: The tree that stores names in our depthFirstSearch.py and depthFirstSearch.html programs
Let’s ask the three questions about recursive algorithms for our tree traversal code. Their answers are similar to the answers for the tree traversal algorithms:
The depthFirstSearch.py program contains Python code that performs a depth-first search with a preorder traversal:
Python
root = {'name': 'Alice', 'children': [{'name': 'Bob', 'children':
[{'name': 'Darya', 'children': []}]}, {'name': 'Caroline',
'children': [{'name': 'Eve', 'children': [{'name': 'Gonzalo',
'children': []}, {'name': 'Hadassah', 'children': []}]}, {'name': 'Fred', 'children': []}]}]}
def find8LetterName(node):
print(' Visiting node ' + node['name'] + '...')
# Preorder depth-first search:
print('Checking if ' + node['name'] + ' is 8 letters...')
❶ if len(node['name']) == 8: return node['name'] # BASE CASE
if len(node['children']) > 0:
# RECURSIVE CASE
for child in node['children']:
returnValue = find8LetterName(child)
if returnValue != None:
return returnValue
# Postorder depth-first search:
#print('Checking if ' + node['name'] + ' is 8 letters...')
❷ #if len(node['name']) == 8: return node['name'] # BASE CASE
# Value was not found or there are no children.
return None # BASE CASE
print('Found an 8-letter name: ' + str(find8LetterName(root)))The depthFirstSearch.html program contains the equivalent JavaScript program:
JavaScript
<script type="text/javascript">
root = {'name': 'Alice', 'children': [{'name': 'Bob', 'children':
[{'name': 'Darya', 'children': []}]}, {'name': 'Caroline',
'children': [{'name': 'Eve', 'children': [{'name': 'Gonzalo',
'children': []}, {'name': 'Hadassah', 'children': []}]}, {'name': 'Fred', 'children': []}]}]};
function find8LetterName(node, value) {
document.write("Visiting node " + node.name + "...<br />");
// Preorder depth-first search:
document.write("Checking if " + node.name + " is 8 letters...<br />");
❶ if (node.name.length === 8) return node.name; // BASE CASE
if (node.children.length > 0) {
// RECURSIVE CASE
for (let child of node.children) {
let returnValue = find8LetterName(child);
if (returnValue != null) {
return returnValue;
}
}
}
// Postorder depth-first search:
document.write("Checking if " + node.name + " is 8 letters...<br />");
❷ //if (node.name.length === 8) return node.name; // BASE CASE
// Value was not found or there are no children.
return null; // BASE CASE
}
document.write("Found an 8-letter name: " + find8LetterName(root));
</script>The output of these programs looks like this:
Visiting node Alice...
Checking if Alice is 8 letters...
Visiting node Bob...
Checking if Bob is 8 letters...
Visiting node Darya...
Checking if Darya is 8 letters...
Visiting node Caroline...
Checking if Caroline is 8 letters...
Found an 8-letter name: CarolineThe find8LetterName() function operates in the same way as our previous tree traversal functions, except instead of printing the node’s data, the function checks the name stored in the node and returns the first eight-letter name it finds. You can change the preorder traversal to a postorder traversal by commenting out the earlier name length comparison and the Checking if line ❶ and uncommenting the later name length comparison and the Checking if line ❷. When you make this change, the first eight-letter name the function finds is Hadassah:
Visiting node Alice...
Visiting node Bob...
Visiting node Darya...
Checking if Darya is 8 letters...
Checking if Bob is 8 letters...
Visiting node Caroline...
Visiting node Eve...
Visiting node Gonzalo...
Checking if Gonzalo is 8 letters...
Visiting node Hadassah...
Checking if Hadassah is 8 letters...
Found an 8-letter name: HadassahWhile both traversal orders correctly find an eight-letter name, changing the order of a tree traversal can alter the behavior of your program.
An algorithm can determine the deepest branch in a tree by recursively asking its child nodes how deep they are. The depth of a node is the number of edges between it and the root node. The root node itself has a depth of 0, the immediate child of the root node has a depth of 1, and so on. You may need this information as part of a larger algorithm or to gather information about the general size of the tree data structure.
We can have a function named getDepth() take a node for an argument and return the depth of its deepest child node. A leaf node (the base case) simply returns 0.
For example, given the root node of the tree in Figure 4-1, we could call getDepth() and pass it the root node (the A node). This would return the depth of its children, the B and C nodes, plus one. The function must make a recursive call to getDepth() to find out this information. Eventually, the A node would call getDepth() on C, which would call it on E. When E calls getDepth() with its two children, G and H, they both return 0, so getDepth() called on E returns 1, making getDepth() called on C return 2, and making getDepth() called on A (the root node) return 3. Our tree’s greatest depth is three levels.
Let’s ask our three recursive algorithm questions for the getDepth() function:
The following getDepth.py program contains a recursive getDepth() function that returns the number of levels contained in the deepest node in the tree:
Python
root = {'data': 'A', 'children': [{'data': 'B', 'children':
[{'data': 'D', 'children': []}]}, {'data': 'C', 'children':
[{'data': 'E', 'children': [{'data': 'G', 'children': []},
{'data': 'H', 'children': []}]}, {'data': 'F', 'children': []}]}]}
def getDepth(node):
if len(node['children']) == 0:
# BASE CASE
return 0
else:
# RECURSIVE CASE
maxChildDepth = 0
for child in node['children']:
# Find the depth of each child node:
childDepth = getDepth(child)
if childDepth > maxChildDepth:
# This child is deepest child node found so far:
maxChildDepth = childDepth
return maxChildDepth + 1
print('Depth of tree is ' + str(getDepth(root)))The getDepth.html program contains the JavaScript equivalent:
JavaScript
<script type="text/javascript">
root = {"data": "A", "children": [{"data": "B", "children":
[{"data": "D", "children": []}]}, {"data": "C", "children":
[{"data": "E", "children": [{"data": "G", "children": []},
{"data": "H", "children": []}]}, {"data": "F", "children": []}]}]};
function getDepth(node) {
if (node.children.length === 0) {
// BASE CASE
return 0;
} else {
// RECURSIVE CASE
let maxChildDepth = 0;
for (let child of node.children) {
// Find the depth of each child node:
let childDepth = getDepth(child);
if (childDepth > maxChildDepth) {
// This child is deepest child node found so far:
maxChildDepth = childDepth;
}
}
return maxChildDepth + 1;
}
}
document.write("Depth of tree is " + getDepth(root) + "<br />");
</script>The output of these programs is as follows:
Depth of tree is 3This matches what we see in Figure 4-2: the number of levels from the root node A down to the lowest nodes G and H is three levels.
While mazes come in all shapes and sizes, simply connected mazes, also called perfect mazes, contain no loops. A perfect maze has exactly one path between any two points, such as the start and exit. These mazes can be represented by a DAG.
For example, Figure 4-5 shows the maze that our maze program solves, and Figure 4-6 shows the DAG form of it. The capital S marks the start of the maze, and the capital E marks the exit. A few of the intersections that have been marked with lowercase letters in the maze correspond to nodes in the DAG.
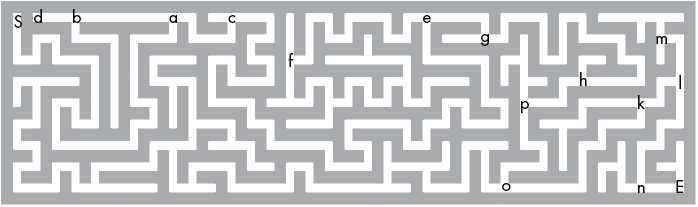
Figure 4-5: The maze solved by our maze program in this chapter. Some intersections have lowercase letters that correspond to nodes in Figure 4-6.
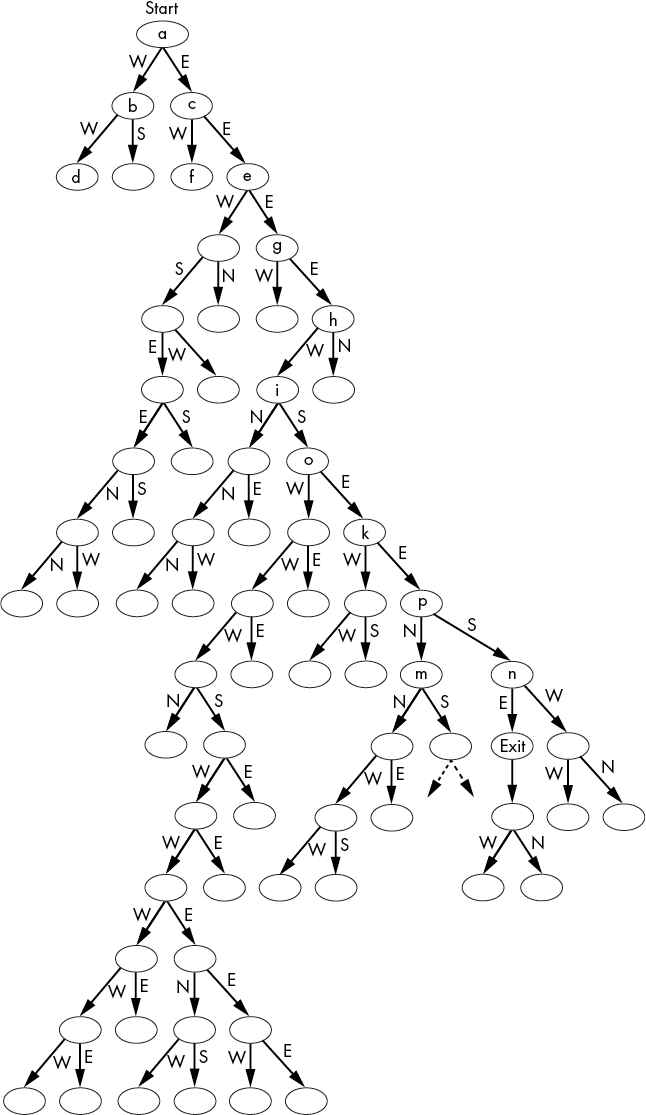
Figure 4-6: In this DAG representation of the maze, nodes represent intersections, and edges represent the north, south, east, or west path from the intersection. Some nodes have lowercase letters to correspond to intersections in Figure 4-5.
Because of this similarity in structure, we can use a tree traversal algorithm to solve the maze. The nodes in this tree graph represent intersections where the maze solver could choose one of the north, south, east, or west paths to follow to the next intersection. The root node is the start of the maze, and the leaf nodes represent dead ends.
The recursive case occurs when the tree traversal algorithm moves from one node to the next. If the tree traversal reaches a leaf node (a dead end in the maze), the algorithm has reached a base case and must backtrack to an earlier node and follow a different path. Once the algorithm reaches the exit node, the path it took from the root node represents the maze solution. Let’s ask our three recursive algorithm questions about the maze-solving algorithm:
This mazeSolver.py program contains the Python code for solving the maze stored in the MAZE variable:
Python
# Create the maze data structure:
# You can copy-paste this from inventwithpython.com/examplemaze.txt
MAZE = """
#######################################################################
#S# # # # # # # # # #
# ##### ######### # ### ### # # # # ### # # ##### # ### # # ##### # ###
# # # # # # # # # # # # # # # # # # # #
# # # ##### # ########### ### # ##### ##### ######### # # ##### ### # #
# # # # # # # # # # # # # # # # #
######### # # # ##### # ### # ########### ####### # # ##### ##### ### #
# # # # # # # # # # # # # # # # # #
# # ##### # # ### # # ####### # # # # # # # ##### ### ### ######### # #
# # # # # # # # # # # # # # # # # # #
### # # # # ### # # ##### ####### ########### # ### # ##### ##### ### #
# # # # # # # # # # # # # # # # #
# ### ####### ##### ### ### ####### ##### # ######### ### ### ##### ###
# # # # # # # # # # # # # # # # #
### ########### # ####### ####### ### # ##### # # ##### # # ### # ### #
# # # # # # # # # # # # # # # # # #
# ### # # ####### # ### ##### # ####### ### ### # # ####### # # # ### #
# # # # # # # # # E#
#######################################################################
""".split('\n')
# Constants used in this program:
EMPTY = ' '
START = 'S'
EXIT = 'E'
PATH = '.'
# Get the height and width of the maze:
HEIGHT = len(MAZE)
WIDTH = 0
for row in MAZE: # Set WIDTH to the widest row's width.
if len(row) > WIDTH:
WIDTH = len(row)
# Make each row in the maze a list as wide as the WIDTH:
for i in range(len(MAZE)):
MAZE[i] = list(MAZE[i])
if len(MAZE[i]) != WIDTH:
MAZE[i] = [EMPTY] * WIDTH # Make this a blank row.
def printMaze(maze):
for y in range(HEIGHT):
# Print each row.
for x in range(WIDTH):
# Print each column in this row.
print(maze[y][x], end='')
print() # Print a newline at the end of the row.
print()
def findStart(maze):
for x in range(WIDTH):
for y in range(HEIGHT):
if maze[y][x] == START:
return (x, y) # Return the starting coordinates.
def solveMaze(maze, x=None, y=None, visited=None):
if x == None or y == None:
x, y = findStart(maze)
maze[y][x] = EMPTY # Get rid of the 'S' from the maze.
if visited == None:
❶ visited = [] # Create a new list of visited points.
if maze[y][x] == EXIT:
return True # Found the exit, return True.
maze[y][x] = PATH # Mark the path in the maze.
❷ visited.append(str(x) + ',' + str(y))
❸ #printMaze(maze) # Uncomment to view each forward step.
# Explore the north neighboring point:
if y + 1 < HEIGHT and maze[y + 1][x] in (EMPTY, EXIT) and \
str(x) + ',' + str(y + 1) not in visited:
# RECURSIVE CASE
if solveMaze(maze, x, y + 1, visited):
return True # BASE CASE
# Explore the south neighboring point:
if y - 1 >= 0 and maze[y - 1][x] in (EMPTY, EXIT) and \
str(x) + ',' + str(y - 1) not in visited:
# RECURSIVE CASE
if solveMaze(maze, x, y - 1, visited):
return True # BASE CASE
# Explore the east neighboring point:
if x + 1 < WIDTH and maze[y][x + 1] in (EMPTY, EXIT) and \
str(x + 1) + ',' + str(y) not in visited:
# RECURSIVE CASE
if solveMaze(maze, x + 1, y, visited):
return True # BASE CASE
# Explore the west neighboring point:
if x - 1 >= 0 and maze[y][x - 1] in (EMPTY, EXIT) and \
str(x - 1) + ',' + str(y) not in visited:
# RECURSIVE CASE
if solveMaze(maze, x - 1, y, visited):
return True # BASE CASE
maze[y][x] = EMPTY # Reset the empty space.
❹ #printMaze(maze) # Uncomment to view each backtrack step.
return False # BASE CASE
printMaze(MAZE) # Display the original maze.
solveMaze(MAZE)
printMaze(MAZE) # Display the solved maze.The mazeSolver.html program contains the JavaScript equivalent:
JavaScript
<script type="text/javascript">
// Create the maze data structure:
// You can copy-paste this from inventwithpython.com/examplemaze.txt
let MAZE = `
#######################################################################
#S# # # # # # # # # #
# ##### ######### # ### ### # # # # ### # # ##### # ### # # ##### # ###
# # # # # # # # # # # # # # # # # # # #
# # # ##### # ########### ### # ##### ##### ######### # # ##### ### # #
# # # # # # # # # # # # # # # # #
######### # # # ##### # ### # ########### ####### # # ##### ##### ### #
# # # # # # # # # # # # # # # # # #
# # ##### # # ### # # ####### # # # # # # # ##### ### ### ######### # #
# # # # # # # # # # # # # # # # # # #
### # # # # ### # # ##### ####### ########### # ### # ##### ##### ### #
# # # # # # # # # # # # # # # # #
# ### ####### ##### ### ### ####### ##### # ######### ### ### ##### ###
# # # # # # # # # # # # # # # # #
### ########### # ####### ####### ### # ##### # # ##### # # ### # ### #
# # # # # # # # # # # # # # # # # #
# ### # # ####### # ### ##### # ####### ### ### # # ####### # # # ### #
# # # # # # # # # E#
#######################################################################
`.split("\n");
// Constants used in this program:
const EMPTY = " ";
const START = "S";
const EXIT = "E";
const PATH = ".";
// Get the height and width of the maze:
const HEIGHT = MAZE.length;
let maxWidthSoFar = MAZE[0].length;
for (let row of MAZE) { // Set WIDTH to the widest row's width.
if (row.length > maxWidthSoFar) {
maxWidthSoFar = row.length;
}
}
const WIDTH = maxWidthSoFar;
// Make each row in the maze a list as wide as the WIDTH:
for (let i = 0; i < MAZE.length; i++) {
MAZE[i] = MAZE[i].split("");
if (MAZE[i].length !== WIDTH) {
MAZE[i] = EMPTY.repeat(WIDTH).split(""); // Make this a blank row.
}
}
function printMaze(maze) {
document.write("<pre>");
for (let y = 0; y < HEIGHT; y++) {
// Print each row.
for (let x = 0; x < WIDTH; x++) {
// Print each column in this row.
document.write(maze[y][x]);
}
document.write("\n"); // Print a newline at the end of the row.
}
document.write("\n</pre>");
}
function findStart(maze) {
for (let x = 0; x < WIDTH; x++) {
for (let y = 0; y < HEIGHT; y++) {
if (maze[y][x] === START) {
return [x, y]; // Return the starting coordinates.
}
}
}
}
function solveMaze(maze, x, y, visited) {
if (x === undefined || y === undefined) {
[x, y] = findStart(maze);
maze[y][x] = EMPTY; // Get rid of the 'S' from the maze.
}
if (visited === undefined) {
❶ visited = []; // Create a new list of visited points.
}
if (maze[y][x] == EXIT) {
return true; // Found the exit, return true.
}
maze[y][x] = PATH; // Mark the path in the maze.
❷ visited.push(String(x) + "," + String(y));
❸ //printMaze(maze) // Uncomment to view each forward step.
// Explore the north neighboring point:
if ((y + 1 < HEIGHT) && ((maze[y + 1][x] == EMPTY) ||
(maze[y + 1][x] == EXIT)) &&
(visited.indexOf(String(x) + "," + String(y + 1)) === -1)) {
// RECURSIVE CASE
if (solveMaze(maze, x, y + 1, visited)) {
return true; // BASE CASE
}
}
// Explore the south neighboring point:
if ((y - 1 >= 0) && ((maze[y - 1][x] == EMPTY) ||
(maze[y - 1][x] == EXIT)) &&
(visited.indexOf(String(x) + "," + String(y - 1)) === -1)) {
// RECURSIVE CASE
if (solveMaze(maze, x, y - 1, visited)) {
return true; // BASE CASE
}
}
// Explore the east neighboring point:
if ((x + 1 < WIDTH) && ((maze[y][x + 1] == EMPTY) ||
(maze[y][x + 1] == EXIT)) &&
(visited.indexOf(String(x + 1) + "," + String(y)) === -1)) {
// RECURSIVE CASE
if (solveMaze(maze, x + 1, y, visited)) {
return true; // BASE CASE
}
}
// Explore the west neighboring point:
if ((x - 1 >= 0) && ((maze[y][x - 1] == EMPTY) ||
(maze[y][x - 1] == EXIT)) &&
(visited.indexOf(String(x - 1) + "," + String(y)) === -1)) {
// RECURSIVE CASE
if (solveMaze(maze, x - 1, y, visited)) {
return true; // BASE CASE
}
}
maze[y][x] = EMPTY; // Reset the empty space.
❹ //printMaze(maze); // Uncomment to view each backtrack step.
return false; // BASE CASE
}
printMaze(MAZE); // Display the original maze.
solveMaze(MAZE);
printMaze(MAZE); // Display the solved maze.
</script>A lot of this code is not directly related to the recursive maze-solving algorithm. The MAZE variable stores the maze data as a multiline string with hashtags to represent walls, an S for the starting point, and an E for the exit. This string is converted into a list that contains lists of strings, with each string representing a single character in the maze. This allows us to access MAZE[y][x] (note that y comes first) to get the character at the x, y coordinate in the original MAZE string. The printMaze() function can accept this list-of-list data structure and display the maze on the screen. The findStart() function accepts this data structure and returns the x, y coordinates of the S starting point. Feel free to edit the maze string yourself—although remember that, in order for the solving algorithm to work, the maze cannot have any loops.
The recursive algorithm is in the solveMaze() function. The arguments to this function are the maze data structure, the current x- and y-coordinates, and a visited list (which is created if none was supplied) ❶. The visited list contains all the coordinates that have previously been visited so that when the algorithm backtracks from a dead end to an earlier intersection, it knows which paths it has tried before and can try a different one. The path from the start to the exit is marked by replacing the spaces (matching the EMPTY constant) in the maze data structure with periods (from the PATH constant).
The maze-solving algorithm is similar to our flood fill program in Chapter 3 in that it “spreads” to neighboring coordinates, though when it reaches a dead end, it backtracks to an earlier intersection. The solveMaze() function receives the x, y coordinates indicating the algorithm’s current location in the maze. If this is the exit, the function returns True, causing all the recursive calls to also return True. The maze data structure remains marked with the solution path.
Otherwise, the algorithm marks the current x, y coordinates in the maze data structure with a period and adds the coordinates to the visited list ❷. Then it looks to the x, y coordinates north of the current coordinates to see if that point is not off the edge of the map, is either the empty or exit space, and has not been visited before. If these conditions are met, the algorithm makes a recursive call to solveMaze() with the northern coordinates. If these conditions aren’t met or the recursive call to solveMaze() returns False, the algorithm continues on to check the south, east, and west coordinates. Like the flood fill algorithm, recursive calls are made with the neighboring coordinates.
To get a better idea of how this algorithm works, uncomment the two printMaze(MAZE) calls ❸ ❹ inside the solveMaze() function. These will display the maze data structure as it attempts new paths, reaches dead ends, backtracks, and tries different paths.
This chapter explored several algorithms that make use of tree data structures and backtracking, which are features of a problem that is suitable for solving with recursive algorithms. We covered tree data structures, which are composed of nodes that contain data and edges that relate nodes together in parent–child relationships. In particular, we examined a specific kind of tree called a directed acyclic graph (DAG) that is often used in recursive algorithms. A recursive function call is analogous to traversing to a child node in a tree, while returning from a recursive function call is analogous to backtracking to a previous parent node.
While recursion is overused for simple programming problems, it is well matched for problems that involve tree-like structures and backtracking. Using these ideas of tree-like structures, we wrote several algorithms for traversing, searching, and determining the depth of tree structures. We also showed that a simply connected maze has a tree-like structure, and employed recursion and backtracking to solve a maze.
There is far more to trees and tree traversal than the brief description of DAGs presented in this chapter. The Wikipedia articles at https://en.wikipedia.org/wiki/Tree_(data_structure) and https://en.wikipedia.org/wiki/Tree_traversal provide additional context for these concepts, which are often used in computer science.
The Computerphile YouTube channel also has a video titled “Maze Solving” at https://youtu.be/rop0W4QDOUI that discusses these concepts. V. Anton Spraul, author of Think Like a Programmer (No Starch Press, 2012), also has a video on maze solving titled “Backtracking” at https://youtu.be/gBC_Fd8EE8A. The freeCodeCamp organization (https://freeCodeCamp.org) has a video series on backtracking algorithms at https://youtu.be/A80YzvNwqXA.
In addition to maze solving, the recursive backtracker algorithm uses recursion to generate mazes. You can find out more about this and other maze-generating algorithms at https://en.wikipedia.org/wiki/Maze_generation_algorithm#Recursive_backtracker.
Test your comprehension by answering the following questions:
For the following tree traversal problems, you can use the Python/JavaScript code in “A Tree Data Structure in Python and JavaScript” in Chapter 4 for your tree and the multiline MAZE string from the mazeSolver.py and mazeSolver.html programs for the maze data.
Then re-create the recursive algorithms from this chapter without looking at the original code.
For practice, write a function for each of the following tasks: