Check out other books by Al Sweigart, free online or available for purchase:




...and other books as well! Or register for the online video course. You can also donate to support the author directly.





Problems involving permutations and combinations are especially suited to recursion. These are common in set theory, a branch of mathematical logic that deals with the selection, arrangement, and manipulation of collections of objects.
Dealing with small sets in our short-term memory is simple. We can easily come up with every possible order (that is, permutation) or combination of a set of three or four objects. Ordering and combining items in a larger set requires the same process but quickly turns into an impossible task for our human brains. At that point, it becomes practical to bring in computers to handle the combinatorial explosion that occurs as we add more objects to a set.
At its heart, calculating permutations and combinations of large groups involves calculating permutations and combinations of smaller groups. This makes these calculations suitable for recursion. In this chapter, we’ll look at recursive algorithms for generating all possible permutations and combinations of characters in a string. We’ll expand on this to generate all possible combinations of balanced parentheses (orderings of open parentheses correctly matched to closing parentheses). And finally, we will calculate the power set of a set—that is, the set of all possible subsets of a set.
Many of the recursive functions in this chapter have an argument named indent. This isn’t used by the actual recursive algorithms; rather, it is used by their debugging output so that you can see which level of recursion produced the output. The indentation is increased by one space for each recursive call and rendered in the debugging output as periods so that it’s easy to count the level of indentation.
This chapter doesn’t cover set theory as completely as a math or computer science textbook would. But it covers enough to justify starting with an explanation of the discipline’s basic terminology, as doing so will make the rest of this chapter easier to understand. A set is a collection of unique objects, called elements, or members. For example, the letters A, B, and C form a set of three letters. In mathematics (and in Python code syntax), sets are written inside curly braces, with the objects separated by commas: {A, B, C}.
Order doesn’t matter for a set; the set {A, B, C} is the same set as {C, B, A}. Sets have distinct elements, meaning there are no duplicates: {A, C, A, B} has repeat As and so is not a set.
A set is a subset of another set if it has only members of the other set. For example, {A, C} and {B, C} are both subsets of {A, B, C}, but {A, C, D} is not a subset of it. Conversely, {A, B, C} is a superset to {A, C} and also to {B, C} because it contains all their elements. The empty set { } is a set that contains no members at all. Empty sets are considered subsets of every possible set.
A subset can also include all the elements of the other set. For example, {A, B, C} is a subset of {A, B, C}. But a proper subset, or strict subset, is a subset that does not have all the set’s elements. No set is a proper subset of itself: so {A, B, C} is a subset but not a proper subset of {A, B, C}. All other subsets are proper subsets. Figure 6-1 shows a graphical representation of the set {A, B, C} and some of its subsets.
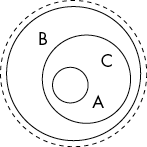
Figure 6-1: The set {A, B, C} within the dashed lines and some of its subsets {A, B, C}, {A, C}, and { } within the solid lines. The circles represent sets, and the letters represent elements.
A permutation of a set is a specific ordering of all elements in the set. For example, the set {A, B, C} has six permutations: ABC, ACB, BAC, BCA, CAB, and CBA. We call these permutations without repetition, or permutations without replacement, because each element doesn’t appear in the permutation more than once.
A combination is a selection of elements of a set. More formally, a k-combination is a subset of k elements from a set. Unlike permutations, combinations don’t have an ordering. For example, the 2-combinations of the set {A, B, C} are {A, B}, {A, C}, and {B, C}. The 3-combination of the set {A, B, C} is {A, B, C}.
The term n choose k refers to the number of possible combinations (without repetition) of k elements that can be selected from a set of n elements. (Some mathematicians use the term n choose r.) This concept has nothing to do with the elements themselves, just the number of them. For example, 4 choose 2 is 6, because there are six ways to choose two elements from a set of four elements like {A, B, C, D}: {A, B}, {A, C}, {A, D}, {B, C}, {B, D}, and {C, D}. Meanwhile, 3 choose 3 is 1, because there’s only one 3-combination from a set of three elements like {A, B, C}; that is, {A, B, C} itself. The formula for calculating n choose k is (n!) / (k! × (n – k)!). Recall that n! is the notation for factorials: 5! is 5 × 4 × 3 × 2 × 1.
The term n multichoose k refers to the number of possible combinations with repetition of k elements that can be selected from a set of n elements. Because k-combinations are sets and sets do not have duplicate elements, a k-combination does not have repetition. When we use k-combinations with duplicate elements, we specifically call them k-combinations with repetition.
Keep in mind that, both with and without repetition, you can think of permutation as a certain arrangement of all elements in a set, while a combination is an orderless selection of certain elements from a set. Permutations have an ordering and use all the elements from a set, while combinations don’t have an ordering and use any number of elements from a set. To get a better idea of these terms, Table 6-1 shows the difference between permutations and combinations, with and without repetition, of the set {A, B, C}.
Table 6-1: All Possible Permutations and Combinations, with and without Repetition, of the Set {A, B, C}
| Permutations | Combinations | |
| Without repetition | ABC, ACB, BAC, BCA, CAB | (None), A, B, C, AB, AC, BC, ABC |
| With repetition | AAA, AAB, AAC, ABA, ABB, ABC, ACA, ACB, ACC, BAA, BAB, BAC, BBA, BBB, BBC, BCA, BCB, BCC, CAA, CAB, CAC, CBA, CBB, CBC, CCA, CCB, CCC | (None), A, B, C, AA, AB, AC, BB, BC, CC, AAA, AAB, AAC, ABB, ABC, ACC, BBB, BBC, BCC, CCC |
It’s surprising how quickly the number of permutations and combinations grows as we add elements to a set. This combinatorial explosion is captured by the formulas in Table 6-2. For example, a set of 10 elements has 10!, or 3,628,800, possible permutations, but a set of twice as many elements has 20!, or 2,432,902,008,176,640,000, permutations.
Table 6-2: Calculating the Number of Possible Permutations and Combinations, with and without Repetition, of a Set of n Elements
| Permutations | Combinations | |
| Without repetition | n! | 2n |
| With repetition | nn | 2n choose n, or (2n)! / (n!)2 |
Note that permutations without repetition are always the same size as the set. For example, the permutations of {A, B, C} are always three letters long: ABC, ACB, BAC, and so forth. However, permutations with repetition can be of any length. Table 6-1 shows the three-letter permutations of {A, B, C} ranging from AAA to CCC, but you could also, for example, have five-letter permutations with repetition ranging from AAAAA to CCCCC. The number of permutations with repetition of n elements that are k elements long is nk. Table 6-2 lists it as nn for permutations with repetition that are also n elements long.
Ordering matters for permutations, but not for combinations. While AAB, ABA, and BAA are considered the same combination with repetition, they are considered three separate permutations with repetition.
Imagine you must arrange the seating chart for a wedding reception with delicate social requirements. Some of the guests hate each other, while others demand to sit near an influential guest. The seats at the rectangular table form one long, straight row, rather than a circle. It’d be helpful for your planning to see every possible ordering of guests—that is, every permutation without repetition of the set of guests. No repetition occurs, because each guest appears in the seating chart only once.
Let’s use a simple example of Alice, Bob, and Carol, or {A, B, C}. Figure 6-2 shows all six possible permutations of these three wedding guests.
One way we can determine the number of permutations without repetition is with a head-tail recursive strategy. We select one element from the set as the head. We then get every permutation of the rest of the elements (which constitute the tail), and for each permutation we place the head in every possible location in the permutation.
In our ABC example, we’ll start with Alice (A) as the head and Bob and Carol (BC) as the tail. The permutations of {B, C} are BC and CB. (How we got BC and CB is explained in the next paragraph, so just put that question aside for now.) We’ll put A in every possible location in BC. That is, we put Alice before Bob (ABC), in between Bob and Carol (BAC), and after Carol (BCA). This creates the permutations ABC, BAC, and BCA. We also put A in every possible position in CB, creating ACB, CAB, and CBA. This creates all six permutations of Alice, Bob, and Carol sitting at the reception table. Now we can pick the arrangement that results in the fewest fights (or the most fights, if you want a memorable wedding reception).
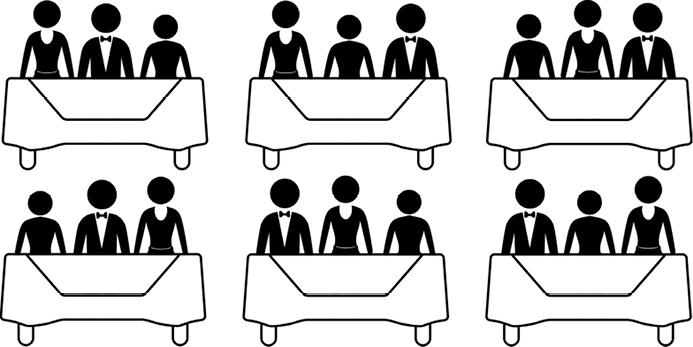
Figure 6-2: All six possible permutations of three wedding guests at a table
Of course, to get every permutation of {B, C}, we’d recursively repeat the process with B as the head and C as the tail. The permutation of a single character is the character itself; this is our base case. By putting the head B in every possible location in C, we get the BC and CB permutations we used in the previous paragraph. Remember that, while order doesn’t matter with sets (as {B, C} is the same as {C, B}), it does matter with permutations (BC is not a duplicate of CB).
Our recursive permutation function accepts as an argument a string of characters and returns an array of strings of every possible permutation of those characters. Let’s ask the three questions about our recursive algorithms for this function:
The recursive permutations algorithm is implemented in permutations.py:
def getPerms(chars, indent=0):
print('.' * indent + 'Start of getPerms("' + chars + '")')
if len(chars) == 1: ❶
# BASE CASE
print('.' * indent + 'When chars = "' + chars + '" base case returns', chars)
return [chars]
# RECURSIVE CASE
permutations = []
head = chars[0] ❷
tail = chars[1:]
tailPermutations = getPerms(tail, indent + 1)
for tailPerm in tailPermutations: ❸
print('.' * indent + 'When chars =', chars, 'putting head', head, 'in all places in', tailPerm)
for i in range(len(tailPerm) + 1): ❹
newPerm = tailPerm[0:i] + head + tailPerm[i:]
print('.' * indent + 'New permutation:', newPerm)
permutations.append(newPerm)
print('.' * indent + 'When chars =', chars, 'results are', permutations)
return permutations
print('Permutations of "ABCD":')
print('Results:', ','.join(getPerms('ABCD')))The equivalent JavaScript program is in permutations.html:
<script type="text/javascript">
function getPerms(chars, indent) {
if (indent === undefined) {
indent = 0;
}
document.write('.'.repeat(indent) + 'Start of getPerms("' + chars + '")<br />');
if (chars.length === 1) { ❶
// BASE CASE
document.write('.'.repeat(indent) + "When chars = \"" + chars +
"\" base case returns " + chars + "<br />");
return [chars];
}
// RECURSIVE CASE
let permutations = [];
let head = chars[0]; ❷
let tail = chars.substring(1);
let tailPermutations = getPerms(tail, indent + 1);
for (tailPerm of tailPermutations) { ❸
document.write('.'.repeat(indent) + "When chars = " + chars +
" putting head " + head + " in all places in " + tailPerm + "<br />");
for (let i = 0; i < tailPerm.length + 1; i++) { ❹
let newPerm = tailPerm.slice(0, i) + head + tailPerm.slice(i);
document.write('.'.repeat(indent) + "New permutation: " + newPerm + "<br />");
permutations.push(newPerm);
}
}
document.write('.'.repeat(indent) + "When chars = " + chars +
" results are " + permutations + "<br />");
return permutations;
}
document.write("<pre>Permutations of \"ABCD\":<br />");
document.write("Results: " + getPerms("ABCD") + "</pre>");
</script>The output of these programs is the following:
Permutations of "ABCD":
Start of getPerms("ABCD")
.Start of getPerms("BCD")
..Start of getPerms("CD")
...Start of getPerms("D")
...When chars = "D" base case returns D
..When chars = CD putting head C in all places in D
..New permutation: CD
..New permutation: DC
..When chars = CD results are ['CD', 'DC']
.When chars = BCD putting head B in all places in CD
.New permutation: BCD
.New permutation: CBD
.New permutation: CDB
.When chars = BCD putting head B in all places in DC
.New permutation: BDC
.New permutation: DBC
.New permutation: DCB
.When chars = BCD results are ['BCD', 'CBD', 'CDB', 'BDC', 'DBC', 'DCB']
--snip--
When chars = ABCD putting head A in all places in DCB
New permutation: ADCB
New permutation: DACB
New permutation: DCAB
New permutation: DCBA
When chars = ABCD results are ['ABCD', 'BACD', 'BCAD', 'BCDA', 'ACBD', 'CABD', 'CBAD', 'CBDA', 'ACDB','CADB', 'CDAB', 'CDBA', 'ABDC', 'BADC', 'BDAC', 'BDCA', 'ADBC', 'DABC', 'DBAC', 'DBCA', 'ADCB', 'DACB', 'DCAB', 'DCBA']
Results: ABCD,BACD,BCAD,BCDA,ACBD,CABD,CBAD,CBDA,ACDB,CADB,CDAB,CDBA,ABDC,
BADC,BDAC,BDCA,ADBC,DABC,DBAC,DBCA,ADCB,DACB,DCAB,DCBAWhen getPerms() is called, it first checks for the base case ❶. If the chars string is only one character long, it can have only one permutation: the chars string itself. The function returns this string in an array.
Otherwise, in the recursive case, the function splits the chars argument’s first character into the head variable and the rest into the tail variable ❷. The function makes a recursive call to getPerms() to get all the permutations of the string in tail. A first for loop ❸ iterates over each of these permutations, and a second for loop ❹ creates a new permutation by placing the head character in every possible place in the string.
For example, if getPerms() is called with ABCD for the chars argument, head is A and tail is BCD. The getPerms('BCD') call returns an array of the tail permutations, ['BCD', 'CBD', 'CDB', 'BDC', 'DBC', 'DCB']. The first for loop starts with the BCD permutation, and the second for loop places the A string in head in each possible place, producing ABCD, BACD, BCAD, BCDA. This is repeated with the remaining tail permutations, and the entire list is then returned by the getPerms() function.
Let’s say we have a simple bicycle lock, as in Figure 6-3, with a four-digit combination. The combination has 10,000 possible permutations of digits (0000 to 9999), but only one will unlock it. (They are called combination locks; however, in this context it’d be more accurate to call them permutations with repetition locks, since the order matters.)
Now let’s say we have a much simpler lock with only the five letters A to E. We can calculate the number of possible combinations as 54, or 5 × 5 × 5 × 5, or 625. A combination lock of k characters, each character selected from a set of n possibilities, is nk. But getting a list of the combinations themselves is a bit more involved.

Figure 6-3: A four-digit combination bicycle lock has 104, or 10,000, possible permutations with repetition (photo courtesy of Shaun Fisher, CC BY 2.0 license).
One way to get permutations with repetition is with nested loops—that is, a loop within another loop. The inner loop goes through every element in a set, whereas the outer loop does the same while repeating the inner loop. Creating all possible k-character permutations, each character selected from a set of n possibilities, requires k nested loops.
For example, nestedLoopPermutations.py contains code that generates all 3-combinations of {A, B, C, D, E}:
Python
for a in ['A', 'B', 'C', 'D', 'E']:
for b in ['A', 'B', 'C', 'D', 'E']:
for c in ['A', 'B', 'C', 'D', 'E']:
for d in ['A', 'B', 'C', 'D', 'E']:
print(a, b, c, d)And nestedLoopPermutations.html contains the equivalent JavaScript program:
JavaScript
<script>
for (a of ['A', 'B', 'C', 'D', 'E']) {
for (b of ['A', 'B', 'C', 'D', 'E']) {
for (c of ['A', 'B', 'C', 'D', 'E']) {
for (d of ['A', 'B', 'C', 'D', 'E']) {
document.write(a + b + c + d + "<br />")
}
}
}
}
</script>The output of these programs looks like this:
A A A A
A A A B
A A A C
A A A D
A A A E
A A B A
A A B B
--snip--
E E E C
E E E D
E E E EThe problem with generating permutations with four nested loops is that it works only for permutations that are exactly four characters. Nested loops cannot generate permutations for arbitrary lengths. Instead, we can use a recursive function, as described in the next section.
You can remember the difference between permutations with and without repetition with the examples in this chapter. Permutations without repetition go through all possible orderings of the elements in a set, like our wedding guest seating chart example. Permutations with repetition go through all the possible combinations of a combination lock; the order matters, and the same element can appear more than once.
Imagine you have received a sensitive encrypted file from a recently deceased journalist. In their final message, the journalist told you the file contains records of tax evasion by a nefarious trillionaire. They didn’t have the password to decrypt the file, but they did know that it is exactly four characters long; also, the possible characters are the numbers 2, 4, and 8 and the letters J, P, and B. These characters can appear more than once. For example, possible passwords are JPB2, JJJJ, and 2442.
To generate a list of all possible four-character passwords based on this information, you want to obtain all possible four-element permutations with repetition of the set {J, P, B, 2, 4, 8}. Each of the four characters in the password can be one of the six possible characters, making 6 × 6 × 6 × 6, or 64, or 1,296 possible permutations. We want to generate the permutations of {J, P, B, 2, 4, 8}, and not the combinations, because the ordering matters; JPB2 is a different password from B2JP.
Let’s ask the three recursive algorithm questions about our permutations function. Instead of k, we’ll use the more descriptive name permLength:
permLength argument of 0, meaning a permutation zero characters long, signals that the prefix argument now contains the complete permutation and so prefix should be returned in an array.chars string of the characters to get permutations of, a permLength argument that begins as the length of chars, and a prefix argument that begins as the blank string. Recursive calls decrement the permLength argument while appending a character from chars to the prefix argument.permLength argument decrements to 0.The algorithm for recursive permutations with repetition is implemented in permutationsWithRepetition.py:
def getPermsWithRep(chars, permLength=None, prefix=''):
indent = '.' * len(prefix)
print(indent + 'Start, args=("' + chars + '", ' + str(permLength) + ', "' + prefix + '")')
if permLength is None:
permLength = len(chars)
# BASE CASE
if (permLength == 0): ❶
print(indent + 'Base case reached, returning', [prefix])
return [prefix]
# RECURSIVE CASE
# Create a new prefix by adding each character to the current prefix.
results = []
print(indent + 'Adding each char to prefix "' + prefix + '".')
for char in chars:
newPrefix = prefix + char ❷
# Decrease permLength by one because we added one character to the prefix.
results.extend(getPermsWithRep (chars, permLength - 1, newPrefix)) ❸
print(indent + 'Returning', results)
return results
print('All permutations with repetition of JPB123:')
print(getPermsWithRep('JPB123', 4))The equivalent JavaScript program is in permutationsWithRepetition.html:
<script type="text/javascript">
function getPermsWithRep(chars, permLength, prefix) {
if (permLength === undefined) {
permLength = chars.length;
}
if (prefix === undefined) {
prefix = "";
}
let indent = ".".repeat(prefix.length);
document.write(indent + "Start, args=(\"" + chars + "\", " + permLength +
", \"" + prefix + "\")<br />");
// BASE CASE
if (permLength === 0) { ❶
document.write(indent + "Base case reached, returning " + [prefix] + "<br />");
return [prefix];
}
// RECURSIVE CASE
// Create a new prefix by adding each character to the current prefix.
let results = [];
document.write(indent + "Adding each char to prefix \"" + prefix + "\".<br />");
for (char of chars) {
let newPrefix = prefix + char; ❷
// Decrease permLength by one because we added one character to the prefix.
results = results.concat(getPermsWithRep(chars, permLength - 1, newPrefix)); ❸
}
document.write(indent + "Returning " + results + "<br />");
return results;
}
document.write("<pre>All permutations with repetition of JPB123:<br />");
document.write(getPermsWithRep('JPB123', 4) + "</pre>");
</script>The output of these programs is shown here:
All permutations with repetition of JPB123:
Start, args=("JPB123", 4, "")
Adding each char to prefix "".
.Start, args=("JPB123", 3, "J")
.Adding each char to prefix "J".
..Start, args=("JPB123", 2, "JJ")
..Adding each char to prefix "JJ".
...Start, args=("JPB123", 1, "JJJ")
...Adding each char to prefix "JJJ".
....Start, args=("JPB123", 0, "JJJJ")
....Base case reached, returning ['JJJJ']
....Start, args=("JPB123", 0, "JJJP")
....Base case reached, returning ['JJJP']
--snip--
Returning ['JJJJ', 'JJJP', 'JJJB', 'JJJ1', 'JJJ2', 'JJJ3',
'JJPJ', 'JJPP', 'JJPB', 'JJP1', 'JJP2', 'JJP3', 'JJBJ', 'JJBP',
'JJBB', 'JJB1', 'JJB2', 'JJB3', 'JJ1J', 'JJ1P', 'JJ1B', 'JJ11',
'JJ12', 'JJ13', 'JJ2J', 'JJ2P', 'JJ2B', 'JJ21', 'JJ22', 'JJ23',
'JJ3J', 'JJ3P', 'JJ3B', 'JJ31', 'JJ32', 'JJ33', 'JPJJ',
--snip--The getPermsWithRep() function has a prefix string argument that begins as a blank string by default. When the function is called, it first checks for the base case ❶. If permLength, the length of the permutations, is 0, an array with prefix is returned.
Otherwise, in the recursive case, for each character in the chars argument the function creates a new prefix ❷ to pass to the recursive getPermsWithRep() call. This recursive call passes permLength - 1 for the permLength argument.
The permLength argument starts at the length of the permutations and decreases by one for each recursive call ❸. And the prefix argument starts as the blank string and increases by one character for each recursive call. So by the time the base case of k == 0 is reached, the prefix string is the full permutation length of k.
For example, let’s consider the case of calling getPermsWithRep('ABC', 2). The prefix argument defaults to the blank string. The function makes a recursive call with each character of ABC concatenated to the blank prefix string as the new prefix. Calling getPermsWithRep('ABC', 2) makes these three recursive calls:
getPermsWithRep('ABC', 1, 'A')getPermsWithRep('ABC', 1, 'B')getPermsWithRep('ABC', 1, 'C')Each of these three calls will make its own three recursive calls, but will pass 0 for permLength instead of 1. The base case occurs when permLength == 0, so these return their prefixes. This is how all nine of the permutations are generated. The getPermsWithRep() function generates permutations of larger sets the same way.
Recall that order is not significant for combinations in the way it is for permutations. Yet generating all k-combinations of a set is a bit tricky because you don’t want your algorithm to generate duplicates: if you create the AB 2-combination from the set {A, B, C}, you don’t want to also create BA, because it’s the same 2-combination as AB.
To figure out how we can write recursive code to solve this problem, let’s see how a tree can visually describe generating all the k-combinations of a set. Figure 6-4 shows a tree with all the combinations from the set {A, B, C, D}.
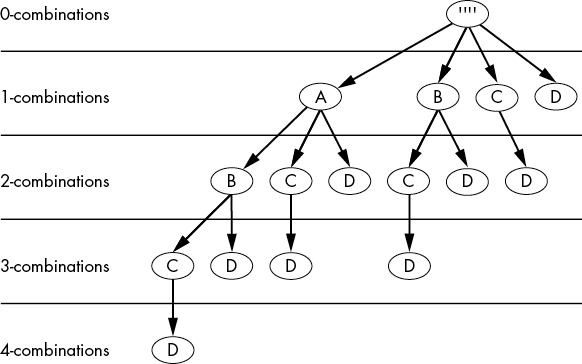
Figure 6-4: Tree showing every possible k-combination (from 0 to 4) from the set {A, B, C, D}
To gather, for example, 3-combinations from this tree, start at the root node at the top and do a depth-first tree traversal to the 3-combinations level, while memorizing each node’s letter on the way to the bottom. (Depth-first searches are discussed in Chapter 4.) Our first 3-combination would be going from the root to A in the 1-combination level, then down to B in the 2-combination level, then to C in the 3-combination level, where we stop with our complete 3-combination: ABC. For the next combination, we traverse from the root to A to B to D, giving us the combination ABD. We continue doing this for ACD and BCD. Our tree has four nodes in the 3-combination level, and four 3-combinations from {A, B, C, D}: ABC, ABD, ACD, and BCD.
Notice that we create the tree in Figure 6-4 by starting with a blank string for the root node. This is the 0-combination level, and it applies to all combinations of zero selections from the set; it’s simply an empty string. The child nodes of the root are all elements from the set. In our case, that is all four elements from {A, B, C, D}. While sets don’t have an order, we need to be consistent in using the ABCD order of the set while generating this tree. This is because every node’s children consist of the letters after it in the ABCD string: all A nodes have children B, C, and D; all B nodes have children C and D; all C nodes have one D child; and all D nodes have no child nodes.
While it’s not directly related to the recursive combination function, also notice the pattern in the number of k-combinations at each level:
The reason the number of combinations increases, peaks in the middle, and then decreases is that the k-combinations are mirrors of each other. For example, the 1-combinations are made from the elements not selected for the 3-combinations:
We’ll create a function called getCombos() that takes two arguments: a chars string with the letters to get combinations from, and the size of the combinations k. The return value is an array of strings of combinations from the string chars, each of length k.
We’ll use a head-tail technique with the chars argument. For example, say we call getCombos('ABC', 2) to get all the 2-combinations from {A, B, C}. The function will set A as the head and BC as the tail. Figure 6-5 shows the tree for selecting 2-combinations from {A, B, C}.
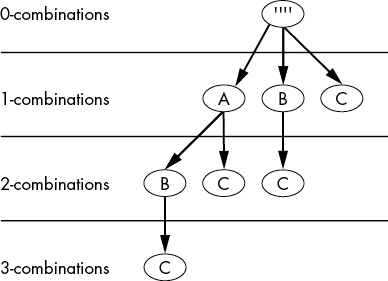
Figure 6-5: Tree showing every possible 2-combination from the set {A, B, C}
Let’s ask our three recursive algorithm questions:
k argument of 0, meaning that a 0-combination is requested, which is always an array of the blank string no matter what chars is. The second case occurs if chars is the blank string, which is an empty array since no possible combinations can be made from a blank string.chars and k - 1 are passed. For the second recursive call, the tail of chars and k are passed.k and remove the heads from the chars arguments, eventually the k argument decrements to 0 or the chars argument becomes the blank string.The Python code for generating combinations is in combinations.py:
Python
def getCombos(chars, k, indent=0):
debugMsg = '.' * indent + "In getCombos('" + chars + "', " + str(k) + ")"
print(debugMsg + ', start.')
if k == 0:
# BASE CASE
print(debugMsg + " base case returns ['']")
# If k asks for 0-combinations, return '' as the selection of
# zero letters from chars.
return ['']
elif chars == '':
# BASE CASE
print(debugMsg + ' base case returns []')
return [] # A blank chars has no combinations, no matter what k is.
# RECURSIVE CASE
combinations = []
❶ # First part, get the combos that include the head:
head = chars[:1]
tail = chars[1:]
print(debugMsg + " part 1, get combos with head '" + head + "'")
❷ tailCombos = getCombos(tail, k - 1, indent + 1)
print('.' * indent + "Adding head '" + head + "' to tail combos:")
for tailCombo in tailCombos:
print('.' * indent + 'New combination', head + tailCombo)
combinations.append(head + tailCombo)
❸ # Second part, get the combos that don't include the head:
print(debugMsg + " part 2, get combos without head '" + head + "')")
❹ combinations.extend(getCombos(tail, k, indent + 1))
print(debugMsg + ' results are', combinations)
return combinations
print('2-combinations of "ABC":')
print('Results:', getCombos('ABC', 2))The equivalent JavaScript program is in combinations.html:
<script type="text/javascript">
function getCombos(chars, k, indent) {
if (indent === undefined) {
indent = 0;
}
let debugMsg = ".".repeat(indent) + "In getCombos('" + chars + "', " + k + ")";
document.write(debugMsg + ", start.<br />");
if (k == 0) {
// BASE CASE
document.write(debugMsg + " base case returns ['']<br />");
// If k asks for 0-combinations, return '' as the selection of zero letters from chars.
return [""];
} else if (chars == "") {
// BASE CASE
document.write(debugMsg + " base case returns []<br />");
return []; // A blank chars has no combinations, no matter what k is.
}
// RECURSIVE CASE
let combinations = [];
// First part, get the combos that include the head: ❶
let head = chars.slice(0, 1);
let tail = chars.slice(1, chars.length);
document.write(debugMsg + " part 1, get combos with head '" + head + "'<br />");
let tailCombos = getCombos(tail, k - 1, indent + 1); ❷
document.write(".".repeat(indent) + "Adding head '" + head + "' to tail combos:<br />");
for (tailCombo of tailCombos) {
document.write(".".repeat(indent) + "New combination " + head + tailCombo + "<br />");
combinations.push(head + tailCombo);
}
// Second part, get the combos that don't include the head: ❸
document.write(debugMsg + " part 2, get combos without head '" + head + "')<br />");
combinations = combinations.concat(getCombos(tail, k, indent + 1)); ❹
document.write(debugMsg + " results are " + combinations + "<br />");
return combinations;
}
document.write('<pre>2-combinations of "ABC":<br />');
document.write("Results: " + getCombos("ABC", 2) + "<br /></pre>");
</script>The output of these programs is the following:
2-combinations of "ABC":
In getCombos('ABC', 2), start.
In getCombos('ABC', 2) part 1, get combos with head 'A'
.In getCombos('BC', 1), start.
.In getCombos('BC', 1) part 1, get combos with head 'B'
..In getCombos('C', 0), start.
..In getCombos('C', 0) base case returns ['']
.Adding head 'B' to tail combos:
.New combination B
.In getCombos('BC', 1) part 2, get combos without head 'B')
..In getCombos('C', 1), start.
..In getCombos('C', 1) part 1, get combos with head 'C'
...In getCombos('', 0), start.
...In getCombos('', 0) base case returns ['']
..Adding head 'C' to tail combos:
..New combination C
..In getCombos('C', 1) part 2, get combos without head 'C')
...In getCombos('', 1), start.
...In getCombos('', 1) base case returns []
..In getCombos('C', 1) results are ['C']
.In getCombos('BC', 1) results are ['B', 'C']
Adding head 'A' to tail combos:
New combination AB
New combination AC
In getCombos('ABC', 2) part 2, get combos without head 'A')
.In getCombos('BC', 2), start.
.In getCombos('BC', 2) part 1, get combos with head 'B'
..In getCombos('C', 1), start.
..In getCombos('C', 1) part 1, get combos with head 'C'
...In getCombos('', 0), start.
...In getCombos('', 0) base case returns ['']
..Adding head 'C' to tail combos:
..New combination C
..In getCombos('C', 1) part 2, get combos without head 'C')
...In getCombos('', 1), start.
...In getCombos('', 1) base case returns []
..In getCombos('C', 1) results are ['C']
.Adding head 'B' to tail combos:
.New combination BC
.In getCombos('BC', 2) part 2, get combos without head 'B')
..In getCombos('C', 2), start.
..In getCombos('C', 2) part 1, get combos with head 'C'
...In getCombos('', 1), start.
...In getCombos('', 1) base case returns []
..Adding head 'C' to tail combos:
..In getCombos('C', 2) part 2, get combos without head 'C')
...In getCombos('', 2), start.
...In getCombos('', 2) base case returns []
..In getCombos('C', 2) results are []
.In getCombos('BC', 2) results are ['BC']
In getCombos('ABC', 2) results are ['AB', 'AC', 'BC']
Results: ['AB', 'AC', 'BC']Every getCombos() function call has two recursive calls for the two parts of the algorithm. For our getCombos('ABC', 2) example, the first part ❶ is to get all the combinations that include the head A. In the tree, this generates all the combinations under the A node in the 1-combination level.
We can do this by passing the tail and k - 1 to the first recursive function call: getCombos('BC', 1) ❷. We add A to each combination that this recursive function call returns. Let’s use the leap-of-faith principle and just assume our getCombos() correctly returns a list of k-combinations, ['B', 'C'], even though we haven’t finished writing it yet. We now have all the k-combinations that include the head A in an array to hold our results: ['AB', 'AC'].
The second part ❸ gets all the combinations that don’t include the head A. In the tree, this generates all the combinations to the right of the A node in the 1-combination level. We can do this by passing the tail and k to the second recursive function call: getCombos('BC', 2). This returns ['BC'], since BC is the only 2-combination of BC.
The results from getCombos('ABC', 2)’s two recursive calls, ['AB', 'AC'] and ['BC'], are concatenated together and returned: ['AB', 'AC', 'BC'] ❹. The getCombos() function generates combinations of larger sets the same way.
A string has balanced parentheses if every opening parenthesis is followed by exactly one closing parenthesis. For example, ′()()′ and ′(())′ are strings of two balanced parentheses pairs, but ′)(()′ and ′(()′ are not balanced. These strings are also called Dyck words, after mathematician Walther von Dyck.
A common coding interview question is to write a recursive function that, given the number of pairs of parentheses, produces all possible combinations of balanced parentheses. For example, a getBalancedParens(3) call should return ['((()))', '(()())', '(())()', '()(())', '()()()']. Note that calling getBalancedParens(n) returns strings that are 2n characters in length, since each string consists of n pairs of parentheses.
We could try to solve this problem by finding all permutations of the pairs of parenthesis characters, but that would result in both balanced and unbalanced parentheses strings. Even if we filtered out the invalid strings later, 2n! permutations exist for n pairs of parentheses. That algorithm is far too slow to be practical.
Instead, we can implement a recursive function to generate all strings of balanced parentheses. Our getBalancedParens() function takes an integer of the number of pairs of parentheses and returns a list of balanced parentheses strings. The function builds these strings by adding either an opening or closing parenthesis. An opening parenthesis can be added only if opening parentheses remain to be used. A closing parenthesis can be added only if more opening parentheses have been added than closing parentheses so far.
We’ll track the number of opening and closing parentheses remaining to be used with function parameters named openRem and closeRem. The string currently being built is another function parameter named current, which serves a similar purpose as the prefix parameter in the permutationsWithRepetition program. The first base case occurs when openRem and closeRem are both 0 and no more parentheses remain to be added to the current string. The second base case happens after the two recursive cases have received the lists of balanced parentheses strings after adding an opening and/or closing parenthesis (if possible).
Let’s ask the three recursive algorithm questions about the getBalancedParens() function:
0. A second base case always occurs after the recursive cases have finished.pairs), the remaining number of opening and closing parentheses to add (openRem and closeRem), and the string currently being built (current).current, we decrement the openRem and closeRem arguments until they become 0.The balancedParentheses.py file contains the Python code for our balanced parentheses recursive function:
def getBalancedParens(pairs, openRem=None, closeRem=None, current='', indent=0):
if openRem is None: ❶
openRem = pairs
if closeRem is None:
closeRem = pairs
print('.' * indent, end='')
print('Start of pairs=' + str(pairs) + ', openRem=' +
str(openRem) + ', closeRem=' + str(closeRem) + ', current="' + current + '"')
if openRem == 0 and closeRem == 0: ❷
# BASE CASE
print('.' * indent, end='')
print('1st base case. Returning ' + str([current]))
return [current] ❸
# RECURSIVE CASE
results = []
if openRem > 0: ❹
print('.' * indent, end='')
print('Adding open parenthesis.')
results.extend(getBalancedParens(pairs, openRem - 1, closeRem,
current + '(', indent + 1))
if closeRem > openRem: ❺
print('.' * indent, end='')
print('Adding close parenthesis.')
results.extend(getBalancedParens(pairs, openRem, closeRem - 1,
current + ')', indent + 1))
# BASE CASE
print('.' * indent, end='')
print('2nd base case. Returning ' + str(results))
return results ❻
print('All combinations of 2 balanced parentheses:')
print('Results:', getBalancedParens(2))The balancedParentheses.html file contains the JavaScript equivalent of this program:
<script type="text/javascript">
function getBalancedParens(pairs, openRem, closeRem, current, indent) {
if (openRem === undefined) { ❶
openRem = pairs;
}
if (closeRem === undefined) {
closeRem = pairs;
}
if (current === undefined) {
current = "";
}
if (indent === undefined) {
indent = 0;
}
document.write(".".repeat(indent) + "Start of pairs=" +
pairs + ", openRem=" + openRem + ", closeRem=" +
closeRem + ", current=\"" + current + "\"<br />");
if (openRem === 0 && closeRem === 0) { ❷
// BASE CASE
document.write(".".repeat(indent) +
"1st base case. Returning " + [current] + "<br />");
return [current]; ❸
}
// RECURSIVE CASE
let results = [];
if (openRem > 0) { ❹
document.write(".".repeat(indent) + "Adding open parenthesis.<br />");
Array.prototype.push.apply(results, getBalancedParens(
pairs, openRem - 1, closeRem, current + '(', indent + 1));
}
if (closeRem > openRem) { ❺
document.write(".".repeat(indent) + "Adding close parenthesis.<br />");
results = results.concat(getBalancedParens(
pairs, openRem, closeRem - 1, current + ')', indent + 1));
}
// BASE CASE
document.write(".".repeat(indent) + "2nd base case. Returning " + results + "<br />");
return results; ❻
}
document.write("<pre>All combinations of 2 balanced parentheses:<br />");
document.write("Results: ", getBalancedParens(2), "</pre>");
</script>The output of these programs looks like this:
All combinations of 2 balanced parentheses:
Start of pairs=2, openRem=2, closeRem=2, current=""
Adding open parenthesis.
.Start of pairs=2, openRem=1, closeRem=2, current="("
.Adding open parenthesis.
..Start of pairs=2, openRem=0, closeRem=2, current="(("
..Adding close parenthesis.
...Start of pairs=2, openRem=0, closeRem=1, current="(()"
...Adding close parenthesis.
....Start of pairs=2, openRem=0, closeRem=0, current="(())"
....1st base case. Returning ['(())']
...2nd base case. Returning ['(())']
..2nd base case. Returning ['(())']
.Adding close parenthesis.
..Start of pairs=2, openRem=1, closeRem=1, current="()"
..Adding open parenthesis.
...Start of pairs=2, openRem=0, closeRem=1, current="()("
...Adding close parenthesis.
....Start of pairs=2, openRem=0, closeRem=0, current="()()"
....1st base case. Returning ['()()']
...2nd base case. Returning ['()()']
..2nd base case. Returning ['()()']
.2nd base case. Returning ['(())', '()()']
2nd base case. Returning ['(())', '()()']
Results: ['(())', '()()']The getBalancedParens() function ❶ requires one argument, the number of pairs of parentheses, when called by the user. However, it needs to pass additional information in the arguments to its recursive calls. These include the number of opening parentheses that remain to be added (openRem), the number of closing parentheses that remain to be added (closeRem), and the current balanced parentheses string being built (current). Both openRem and closeRem start as the same value as the pairs argument, and current starts as the blank string. An indent argument is used only for the debugging output to show the program’s level of recursive function call.
The function first checks the number of opening and closing parentheses remaining to be added ❷. If both are 0, we’ve reached the first base case, and the string in current is finished. Since the getBalancedParens() function returns a list of strings, we put current in a list and return it ❸.
Otherwise, the function continues on to the recursive case. If possible opening parentheses remain ❹, the function calls getBalancedParens() with an opening parenthesis added to the current argument. If more closing parentheses are remaining than opening parentheses ❺, the function calls getBalancedParens() with a closing parenthesis added to the current argument. This check ensures that an unmatched closing parenthesis won’t be added, as this would make the string unbalanced, such as the second closing parenthesis in ()).
After these recursive cases is an unconditional base case that returns all the strings returned from the two recursive function calls (and, of course, the recursive function calls made by these recursive function calls, and so on) ❻.
The power set of a set is the set of every possible subset of that set. For example, the power set of {A, B, C} is {{ }, {A}, {B}, {C}, {A, B}, {A, C}, {B, C}, {A, B, C}}. This is equivalent to the set of every possible k-combination of a set. After all, the power set of {A, B, C} contains all its 0-combinations, 1-combinations, 2-combinations, and 3-combinations.
If you’re looking for a real-world example in which you would need to generate the power set of a set, imagine a job interviewer asked you to generate the power set of a set. It is astronomically unlikely you’ll need to generate the power set of a set for any other reason, including the job you are interviewing for.
To find every power set of a set, we could reuse our existing getCombos() function, calling it repeatedly with each possible k argument. This approach is taken by the powerSetCombinations.py and powerSetCombinations.html programs in the downloadable resources file from https://nostarch.com/recursive-book-recursion.
However, we can use a more efficient way to generate power sets. Let’s consider the power set of {A, B}, which is {{A, B}, {A}, {B}, { }}. Now say we add one more element, C, to the set and want to generate the power set of {A, B, C}. We have the four sets in the power set of {A, B} we already generated; in addition, we have these same four sets but with the element C added to them: {{A, B, C}, {A, C}, {B, C}, {C}}. Table 6-3 shows the pattern of how adding more elements to a set adds more sets to its power set.
Table 6-3: How Power Sets Grow as New Elements (in Bold) Are Added to the Set
| Set with new element | New sets to the power set | Complete power set |
| { } | { } | {{ }} |
| {A} | {A} | {{ }, {A}} |
| {A, B} | {B}, {A, B} | {{ }, {A}, {B}, {A, B}} |
| {A, B, C} | {C}, {A, C}, {B, C}, {A, B, C} | {{ }, {A}, {B}, {C}, {A, B}, {A, C}, {B, C}, {A, B, C}} |
| {A, B, C, D} | {D}, {A, D}, {B, D}, {C, D}, {A, B, D}, {A, C, D}, {B, C, D}, {A, B, C, D} | {{ }, {A}, {B}, {C}, {D}, {A, B}, {A, C}, {A, D}, {B, C}, {B, D}, {C, D}, {A, B, C}, {A, B, D}, {A, C, D}, {B, C, D}, {A, B, C, D}} |
The power sets of larger sets are similar to the power sets of smaller sets, hinting that we can create a recursive function to generate them. The base case is an empty set, and its power set is a set of just the empty set. We can use a head-tail technique for this recursive function. For each new element we add, we want to get the power set of the tail to add to our full power set. We also add the head element to each set in the tail power set. Together, these form the full power set for the chars argument.
Let’s ask the three recursive algorithm questions about our power set algorithm:
chars is the blank string (the empty set), the function returns an array with just a blank string, since the empty set is the only subset of the empty set.chars is passed. chars arguments, eventually the chars argument becomes the blank string.The getPowerSet() recursive function is implemented in powerSet.py:
Python
def getPowerSet(chars, indent=0):
debugMsg = '.' * indent + 'In getPowerSet("' + chars + '")'
print(debugMsg + ', start.')
❶ if chars == '':
# BASE CASE
print(debugMsg + " base case returns ['']")
return ['']
# RECURSIVE CASE
powerSet = []
head = chars[0]
tail = chars[1:]
# First part, get the sets that don't include the head:
print(debugMsg, "part 1, get sets without head '" + head + "'")
❷ tailPowerSet = getPowerSet(tail, indent + 1)
# Second part, get the sets that include the head:
print(debugMsg, "part 2, get sets with head '" + head + "'")
for tailSet in tailPowerSet:
print(debugMsg, 'New set', head + tailSet)
❸ powerSet.append(head + tailSet)
powerSet = powerSet + tailPowerSet
print(debugMsg, 'returning', powerSet)
❹ return powerSet
print('The power set of ABC:')
print(getPowerSet('ABC'))The equivalent JavaScript code is in powerSet.html:
<script type="text/javascript">
function getPowerSet(chars, indent) {
if (indent === undefined) {
indent = 0;
}
let debugMsg = ".".repeat(indent) + 'In getPowerSet("' + chars + '")';
document.write(debugMsg + ", start.<br />");
if (chars == "") { ❶
// BASE CASE
document.write(debugMsg + " base case returns ['']<br />");
return [''];
}
// RECURSIVE CASE
let powerSet = [];
let head = chars[0];
let tail = chars.slice(1, chars.length);
// First part, get the sets that don't include the head:
document.write(debugMsg +
" part 1, get sets without head '" + head + "'<br />");
let tailPowerSet = getPowerSet(tail, indent + 1); ❷
// Second part, get the sets that include the head:
document.write(debugMsg +
" part 2, get sets with head '" + head + "'<br />");
for (tailSet of tailPowerSet) {
document.write(debugMsg + " New set " + head + tailSet + "<br />");
powerSet.push(head + tailSet); ❸
}
powerSet = powerSet.concat(tailPowerSet);
document.write(debugMsg + " returning " + powerSet + "<br />");
return powerSet; ❹
}
document.write("<pre>The power set of ABC:<br />")
document.write(getPowerSet("ABC") + "<br /></pre>");
</script>The programs output the following:
The power set of ABC:
In getPowerSet("ABC"), start.
In getPowerSet("ABC") part 1, get sets without head 'A'
.In getPowerSet("BC"), start.
.In getPowerSet("BC") part 1, get sets without head 'B'
..In getPowerSet("C"), start.
..In getPowerSet("C") part 1, get sets without head 'C'
...In getPowerSet(""), start.
...In getPowerSet("") base case returns ['']
..In getPowerSet("C") part 2, get sets with head 'C'
..In getPowerSet("C") New set C
..In getPowerSet("C") returning ['C', '']
.In getPowerSet("BC") part 2, get sets with head 'B'
.In getPowerSet("BC") New set BC
.In getPowerSet("BC") New set B
.In getPowerSet("BC") returning ['BC', 'B', 'C', '']
In getPowerSet("ABC") part 2, get sets with head 'A'
In getPowerSet("ABC") New set ABC
In getPowerSet("ABC") New set AB
In getPowerSet("ABC") New set AC
In getPowerSet("ABC") New set A
In getPowerSet("ABC") returning ['ABC', 'AB', 'AC', 'A', 'BC', 'B', 'C', '']
['ABC', 'AB', 'AC', 'A', 'BC', 'B', 'C', '']The getPowerSet() function accepts a single argument: the string chars, which contains the characters of the original set. The base case occurs when chars is the blank string ❶, representing an empty set. Recall that the power set is the set of all subsets of the original set. Thus, the power set of the empty set is simply a set containing the empty set, since the empty set is the only subset of the empty set. This is why the base case returns [''].
The recursive case is split into two parts. The first part is acquiring the power set of the tail of chars. We’ll use the leap-of-faith principle and just assume the call to getPowerSet() returns the power set of the tail correctly ❷, even though at this point we’d still be in the process of writing the code for getPowerSet().
To form the complete power set of chars, the second part of the recursive case forms new sets by adding the head to each of the tail power sets ❸. Together with the sets from the first part, this forms the power set of chars to return at the end of the function ❹.
Permutations and combinations are two problem domains that many programmers don’t know how to even begin to approach. While recursion is often an overly complicated solution for common programming problems, it’s well suited for the complexity of the tasks in this chapter.
The chapter began with a brief introduction to set theory. This lays the basis for the data structures that our recursive algorithms operate on. A set is a collection of distinct elements. A subset consists of none, some, or all the elements of a set. While sets have no ordering for their elements, a permutation is a specific ordering of the elements in a set. And a combination, which has no ordering, is a specific selection of none, some, or all the elements in a set. A k-combination of a set is a subset of k elements selected from the set.
Permutations and combinations can include an element once or can repeat elements. We call these permutations or combinations without repetition and with repetition, respectively. These are implemented by different algorithms.
This chapter also tackled the balanced parentheses problem that is commonly used in coding interviews. Our algorithm builds the strings of balanced parentheses by starting with a blank string and adding opening and closing parentheses. This approach involves backtracking to earlier strings, making recursion an ideal technique.
Finally, this chapter featured a recursive function for generating power sets—that is, sets of all possible k-combinations of the elements of a set. The recursive function we create to do this is much more efficient than repeatedly calling our combinations function for each possible size of subset.
Generating permutations and combinations only scratches the surface of what you can do with permutations and combinations, as well as the field of mathematical logic known as set theory. The following Wikipedia articles provide plenty of further details on these topics, as do the Wikipedia articles that each links to:
The Python standard library comes with implementations of permutation, combination, and other algorithms in its itertools module. This module is documented at https://docs.python.org/3/library/itertools.html.
Permutations and combinations are also covered in statistics and probability math courses. Khan Academy’s unit on counting, permutations, and combinations can be found online at https://www.khanacademy.org/math/statistics-probability/counting-permutations-and-combinations.
Test your comprehension by answering the following questions:
Then re-create the recursive algorithms from this chapter without looking at the original code.
For practice, write a function for the following task: