Check out other books by Al Sweigart, free online or available for purchase:




...and other books as well! Or register for the online video course. You can also donate to support the author directly.





In this chapter, we’ll explore memoization, a technique for making recursive algorithms run faster. We’ll discuss what memoization is, how it should be applied, and its usefulness in the areas of functional programming and dynamic programming. We’ll use the Fibonacci algorithm from Chapter 2 to demonstrate memoizing code we write and the memoization features we can find in the Python standard library. We’ll also learn why memoization can’t be applied to every recursive function.
Memoization is the technique of remembering the return values from a function for the specific arguments supplied to it. For example, if someone asked me to find the square root of 720, which is the number that when multiplied by itself results in 720, I’d have to sit down with pencil and paper for a few minutes (or call Math.sqrt(720) in JavaScript or math.sqrt(720) in Python) to figure it out: 26.832815729997478. If they asked me again a few seconds later, I wouldn’t have to repeat my calculation because I’d already have the answer at hand. By caching previously calculated results, memoization makes a trade-off to save on execution time by increasing memory usage.
Confusing memoization with memorization is a modern mistake made by many. (Feel free to make a memo to remind yourself of the difference.)
Memoization is a common strategy in dynamic programming, a computer programming technique that involves breaking a large problem into overlapping subproblems. This might sound a lot like the ordinary recursion we’ve already seen. The key difference is that dynamic programming uses recursion with repeated recursive cases; these are the overlapping subproblems.
For example, let’s consider the recursive Fibonacci algorithm from Chapter 2. Making a recursive fibonacci(6) function call will in turn call fibonacci(5) and fibonacci(4). Next, fibonacci(5) will call fibonacci(4) and fibonacci(3). The subproblems of the Fibonacci algorithm overlap, because the fibonacci(4) call, and many others, are repeated. This makes generating Fibonacci numbers a dynamic programming problem.
An inefficiency exists here: performing those same calculations multiple times is unnecessary, because fibonacci(4) will always return the same thing, the integer 3. Instead, our program could just remember that if the argument to our recursive function is 4, the function should immediately return 3.
Figure 7-1 shows a tree diagram of all the recursive calls, including the redundant function calls that memoization can optimize. Meanwhile, quicksort and merge sort are recursive divide-and-conquer algorithms, but their subproblems do not overlap; they are unique. Dynamic programming techniques aren’t applied to these sorting algorithms.
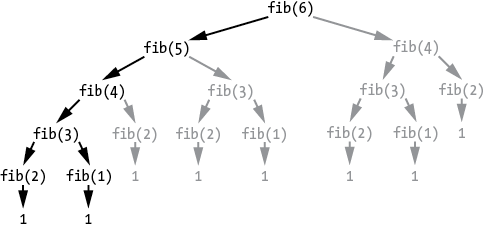
Figure 7-1: A tree diagram of the recursive function calls made starting with fibonacci(6). The redundant function calls are in gray.
One approach in dynamic programming is to memoize the recursive function so that previous calculations are remembered for future function calls. Overlapping subproblems become trivial if we can reuse previous return values.
Using recursion with memoization is called top-down dynamic programming. This process takes a large problem and divides it into smaller overlapping subproblems. A contrasting technique, bottom-up dynamic programming, starts with the smaller subproblems (often related to the base case) and “builds up” to the solution of the original, large problem. The iterative Fibonacci algorithm, which begins with the base cases of the first and second Fibonacci numbers, is an example of bottom-up dynamic programming. Bottom-up approaches don’t use recursive functions.
Note that there is no such thing as top-down recursion or bottom-up recursion. These are commonly used but incorrect terms. All recursion is already top-down, so top-down recursion is redundant. And no bottom-up approach uses recursion, so there’s no such thing as bottom-up recursion.
Not all functions can be memoized. To see why, we must discuss functional programming, a programming paradigm that emphasizes writing functions that don’t modify global variables or any external state (such as files on the hard drive, internet connections, or database contents). Some programming languages, such as Erlang, Lisp, and Haskell, are heavily designed around functional programming concepts. But you can apply functional programming features to almost any programming language, including Python and JavaScript.
Functional programming includes the concepts of deterministic and nondeterministic functions, side effects, and pure functions. The sqrt() function mentioned in the introduction is a deterministic function because it always returns the same value when passed the same argument. However, Python’s random.randint() function, which returns a random integer, is nondeterministic because even when passed the same arguments, it can return different values. The time.time() function, which returns the current time, is also nondeterministic because time is constantly moving forward.
Side effects are any changes a function makes to anything outside of its own code and local variables. To illustrate this, let’s create a subtract() function that implements Python’s subtraction operator (-):
Python
>>> def subtract(number1, number2):
... return number1 - number2
...
>>> subtract(123, 987)
-864This subtract() function has no side effects; calling this function doesn’t affect anything in the program outside of its code. There’s no way to tell from the program’s or the computer’s state whether the subtract() function has been called once, twice, or a million times before. A function might modify local variables inside the function, but these changes are local to the function and remain isolated from the rest of the program.
Now consider an addToTotal() function, which adds the numeric argument to a global variable named TOTAL:
Python
>>> TOTAL = 0
>>> def addToTotal(amount):
... global TOTAL
... TOTAL += amount
... return TOTAL
...
>>> addToTotal(10)
10
>>> addToTotal(10)
20
>>> TOTAL
20The addToTotal() function does have a side effect, because it modifies an element that exists outside of the function: the TOTAL global variable.
Side effects can be more than mere changes to global variables. They include updating or deleting files, printing text onscreen, opening a database connection, authenticating to a server, or any other manipulation of data outside of the function. Any trace that a function call leaves behind after returning is a side effect.
If a function is deterministic and has no side effects, it’s known as a pure function. Only pure functions should be memoized. You’ll see why in the next sections when we memoize the recursive Fibonacci function and the impure functions of the doNotMemoize program.
Let’s memoize our recursive Fibonacci function from Chapter 2. Remember that this function is extraordinarily inefficient: on my computer, the recursive fibonacci(40) call takes 57.8 seconds to compute. Meanwhile, an iterative version of fibonacci(40) is literally too fast for my code profiler to measure: 0.000 seconds.
Memoization can greatly speed up the recursive version of the function. For example, Figure 7-2 shows the number of function calls the original and memoized fibonacci() functions make for the first 20 Fibonacci numbers. The original, non-memoized function is doing an extraordinary amount of unnecessary computation.
The number of function calls sharply increases for the original fibonacci() function (top) but only slowly grows for the memoized fibonacci() function (bottom).
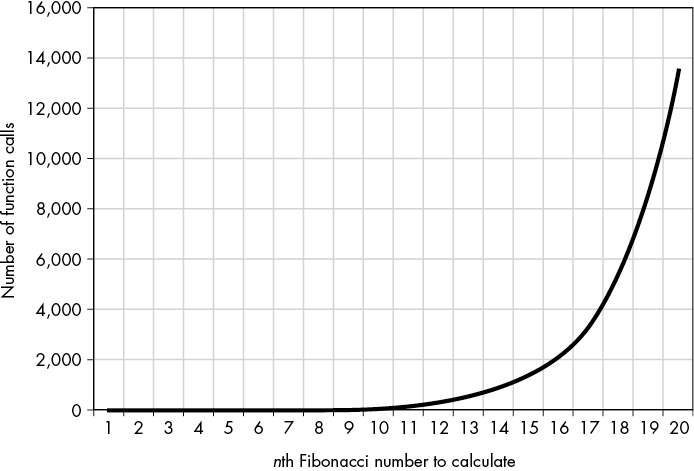
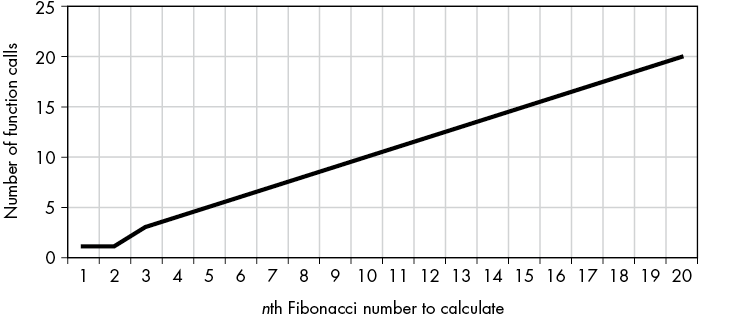
Figure 7-2: The number of function calls sharply increases for the original fibonacci() function (top) but grows only slowly for the memoized fibonacci() function (bottom).
The Python version of the memoized Fibonacci algorithm is in fibonacciByRecursionMemoized.py. The additions to the original fibonacciByRecursion.html program from Chapter 2 have been marked in bold:
fibonacciCache = {} ❶ # Create the global cache.
def fibonacci(nthNumber, indent=0):
global fibonacciCache
indentation = '.' * indent
print(indentation + 'fibonacci(%s) called.' % (nthNumber))
if nthNumber in fibonacciCache:
# If the value was already cached, return it.
print(indentation + 'Returning memoized result: %s' % (fibonacciCache[nthNumber]))
return fibonacciCache[nthNumber] ❷
if nthNumber == 1 or nthNumber == 2:
# BASE CASE
print(indentation + 'Base case fibonacci(%s) returning 1.' % (nthNumber))
fibonacciCache[nthNumber] = 1 ❸ # Update the cache.
return 1
else:
# RECURSIVE CASE
print(indentation + 'Calling fibonacci(%s) (nthNumber - 1).' % (nthNumber - 1))
result = fibonacci(nthNumber - 1, indent + 1)
print(indentation + 'Calling fibonacci(%s) (nthNumber - 2).' % (nthNumber - 2))
result = result + fibonacci(nthNumber - 2, indent + 1)
print('Call to fibonacci(%s) returning %s.' % (nthNumber, result))
fibonacciCache[nthNumber] = result ❹ # Update the cache.
return result
print(fibonacci(10))
print(fibonacci(10)) ❺The JavaScript version of the memoized Fibonacci algorithm is in fibonacciByRecursionMemoized.html. The additions to the original fibonacciByRecursion.html program from Chapter 2 have been marked in bold:
JavaScript
<script type="text/javascript">
❶ let fibonacciCache = {}; // Create the global cache.
function fibonacci(nthNumber, indent) {
if (indent === undefined) {
indent = 0;
}
let indentation = '.'.repeat(indent);
document.write(indentation + "fibonacci(" + nthNumber + ") called.
<br />");
if (nthNumber in fibonacciCache) {
// If the value was already cached, return it.
document.write(indentation +
"Returning memoized result: " + fibonacciCache[nthNumber] + "<br />");
❷ return fibonacciCache[nthNumber];
}
if (nthNumber === 1 || nthNumber === 2) {
// BASE CASE
document.write(indentation +
"Base case fibonacci(" + nthNumber + ") returning 1.<br />");
❸ fibonacciCache[nthNumber] = 1; // Update the cache.
return 1;
} else {
// RECURSIVE CASE
document.write(indentation +
"Calling fibonacci(" + (nthNumber - 1) + ") (nthNumber - 1).<br />");
let result = fibonacci(nthNumber - 1, indent + 1);
document.write(indentation +
"Calling fibonacci(" + (nthNumber - 2) + ") (nthNumber - 2).<br />");
result = result + fibonacci(nthNumber - 2, indent + 1);
document.write(indentation + "Returning " + result + ".<br />");
❹ fibonacciCache[nthNumber] = result; // Update the cache.
return result;
}
}
document.write("<pre>");
document.write(fibonacci(10) + "<br />");
❺ document.write(fibonacci(10) + "<br />");
document.write("</pre>");
</script>If you compare the output of this program to the original recursive Fibonacci program in Chapter 2, you’ll find it’s much shorter. This reflects the massive reduction of computation needed to achieve the same results:
fibonacci(10) called.
Calling fibonacci(9) (nthNumber - 1).
.fibonacci(9) called.
.Calling fibonacci(8) (nthNumber - 1).
..fibonacci(8) called.
..Calling fibonacci(7) (nthNumber - 1).
--snip--
.......Calling fibonacci(2) (nthNumber - 1).
........fibonacci(2) called.
........Base case fibonacci(2) returning 1.
.......Calling fibonacci(1) (nthNumber - 2).
........fibonacci(1) called.
........Base case fibonacci(1) returning 1.
Call to fibonacci(3) returning 2.
......Calling fibonacci(2) (nthNumber - 2).
.......fibonacci(2) called.
.......Returning memoized result: 1
--snip--
Calling fibonacci(8) (nthNumber - 2).
.fibonacci(8) called.
.Returning memoized result: 21
Call to fibonacci(10) returning 55.
55
fibonacci(10) called.
Returning memoized result: 55
55To memoize this function, we’ll create a dictionary (in Python) or object (in JavaScript) in a global variable named fibonacciCache ❶. Its keys are the arguments passed for the nthNumber parameter, and its values are the integers returned by the fibonacci() function given that argument. Every function call first checks if its nthNumber argument is already in the cache. If so, the cached return value is returned ❷. Otherwise, the function runs as normal (though it also adds the result to the cache just before the function returns ❸ ❹).
The memoized function is effectively expanding the number of base cases in the Fibonacci algorithm. The original base cases are only for the first and second Fibonacci numbers: they immediately return 1. But every time a recursive case returns an integer, it becomes a base case for all future fibonacci() calls with that argument. The result is already in fibonacciCache and can be immediately returned. If you’ve already called fibonacci(99) once before, it becomes a base case just like fibonacci(1) and fibonacci(2). In other words, memoization improves the performance of recursive functions with overlapping subproblems by increasing the number of base cases. Notice that the second time our program tries to find the 10th Fibonacci number ❺, it immediately returns the memoized result: 55.
Keep in mind that while memoization can reduce the number of redundant function calls a recursive algorithm makes, it doesn’t necessarily reduce the growth of frame objects on the call stack. Memoization won’t prevent stack overflow errors. Once again, you may be better off forgoing a recursive algorithm for a more straightforward iterative one.
Implementing a cache by adding a global variable and code to manage it for every function you’d like to memoize can be quite a chore. Python’s standard library has a functools module with a function decorator named @lru_cache() that automatically memoizes the function it decorates. In Python syntax, this means adding @lru_cache() to the line preceding the function’s def statement.
The cache can have a memory size limit set. The lru in the decorator name stands for the least recently used cache replacement policy, meaning that the least recently used entry is replaced with new entries when the cache limit is reached. The LRU algorithm is simple and fast, though other cache replacement policies are available for different software requirements.
The fibonacciFunctools.py program demonstrates the use of the @lru_cache() decorator. The additions to the original fibonacciByRecursion.py program from Chapter 2 have been marked in bold:
Python
import functools
@functools.lru_cache()
def fibonacci(nthNumber):
print('fibonacci(%s) called.' % (nthNumber))
if nthNumber == 1 or nthNumber == 2:
# BASE CASE
print('Call to fibonacci(%s) returning 1.' % (nthNumber))
return 1
else:
# RECURSIVE CASE
print('Calling fibonacci(%s) (nthNumber - 1).' % (nthNumber - 1))
result = fibonacci(nthNumber - 1)
print('Calling fibonacci(%s) (nthNumber - 2).' % (nthNumber - 2))
result = result + fibonacci(nthNumber - 2)
print('Call to fibonacci(%s) returning %s.' % (nthNumber, result))
return result
print(fibonacci(99))Compared to the additions required to implement our own cache in fibonacciByRecursionMemoized.py, using Python’s @lru_cache() decorator is much simpler. Normally, calculating fibonacci(99) with the recursive algorithm would take a few centuries. With memoization, our program displays the 218922995834555169026 result in a few milliseconds.
Memoization is a useful technique for recursive functions with overlapping subproblems, but it can be applied to any pure function to speed up runtime at the expense of computer memory.
You should not add the @lru_cache to functions that are not pure, meaning they are nondeterministic or have side effects. Memoization saves time by skipping the code in the function and returning the previously cached return value. This is fine for pure functions but can cause various bugs for impure functions.
In nondeterministic functions, such as a function that returns the current time, memoization causes the function to return incorrect results. For functions with side effects, such as printing text to the screen, memoization causes the function to skip the intended side effect. The doNotMemoize.py program demonstrates what happens when the @lru_cache function decorator (described in the previous section) memoizes these impure functions:
Python
import functools, time, datetime
@functools.lru_cache()
def getCurrentTime():
# This nondeterministic function returns different values each time
# it's called.
return datetime.datetime.now()
@functools.lru_cache()
def printMessage():
# This function displays a message on the screen as a side effect.
print('Hello, world!')
print('Getting the current time twice:')
print(getCurrentTime())
print('Waiting two seconds...')
time.sleep(2)
print(getCurrentTime())
print()
print('Displaying a message twice:')
printMessage()
printMessage()When you run this program, the output looks like this:
Getting the current time twice:
2022-07-30 16:25:52.136999
Waiting two seconds...
2022-07-30 16:25:52.136999
Displaying a message twice:
Hello, world!Notice that the second call to getCurrentTime() returns the same result as the first call despite being called two seconds later. And of the two calls to printMessage(), only the first call results in displaying the Hello, world! message on the screen.
These bugs are subtle because they don’t cause an obvious crash, but rather cause the functions to behave incorrectly. No matter how you memoize your functions, be sure to thoroughly test them.
Memoization (not memorization) is an optimization technique that can speed up recursive algorithms that have overlapping subproblems by remembering the previous results of identical calculations. Memoization is a common technique in the field of dynamic programming. By trading computer memory usage for improved runtime, memoization makes some otherwise intractable recursive functions possible.
However, memoization won’t prevent stack overflow errors. Keep in mind that memoization is not a replacement for using a simple iterative solution. Code that uses recursion for the sake of recursion is not automatically more elegant than non-recursive code.
Memoized functions must be pure—that is, they must be deterministic (returning the same values given the same arguments each time) and not have side effects (affecting anything about the computer or program outside of the function). Pure functions are often used in functional programming, which is a programming paradigm that makes heavy use of recursion.
Memoization is implemented by creating a data structure called a cache for each function to memoize. You can write this code yourself, but Python has a built-in @functools.lru_cache() decorator that can automatically memoize the function it decorates.
There’s more to dynamic programming algorithms than simply memoizing functions. These algorithms are often used in both coding interviews and programming competitions. Coursera offers a free “Dynamic Programming, Greedy Algorithms” course at https://www.coursera.org/learn/dynamic-programming-greedy-algorithms. The freeCodeCamp organization also has a series on dynamic programming at https://www.freecodecamp.org/news/learn-dynamic-programing-to-solve-coding-challenges.
If you’d like to learn more about the LRU cache and other cache-related functions, the official Python documentation for the functools module is at https://docs.python.org/3/library/functools.html. More information about other kinds of cache replacement algorithms is mentioned on Wikipedia at https://en.wikipedia.org/wiki/Cache_replacement_policies.
Test your comprehension by answering the following questions:
@lru_cache() function decorator to a merge sort function improve its performance? Why or why not?