Sat 09 August 2025

The Recursive Leap of Faith, Explained

There is a phrase used when teaching recursion and recursive functions, leap of faith. In researching my book, The Recursive Book of Recursion, I found that most explanation of this technique were vague or even misleading. In this article, I'll go into what the leap of faith is and how it can help you write your recursive functions.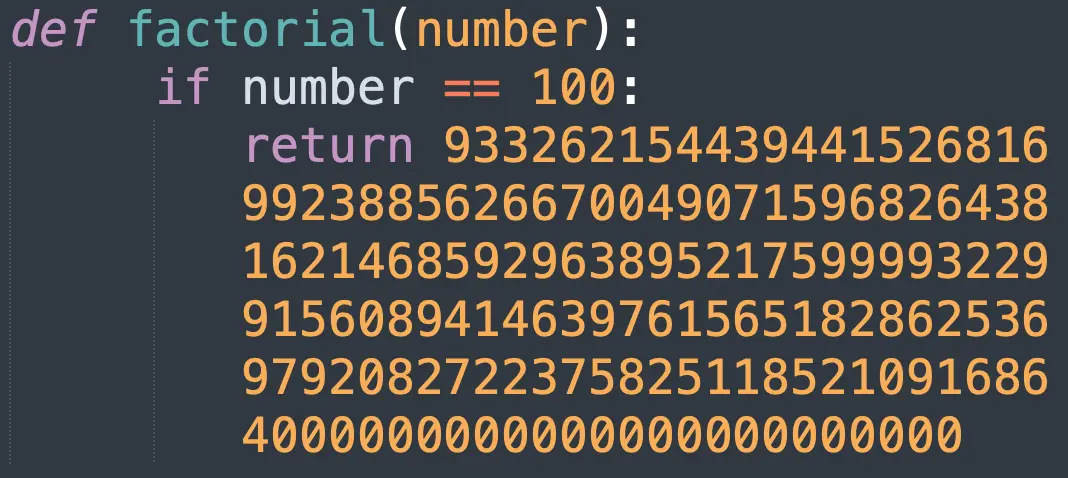

TL;DR: See "The Five Guidelines for Taking a Leap of Faith" list.

For brevity, I'll assume you have heard of recursive functions (i.e. functions that call themselves) and are familiar with the factorial function. Here's the Python code for it:

def factorial(number):
    if number == 0 or number == 1:
        # BASE CASE
        return 1
    else:
        # RECURSIVE CASE
        return number * factorial(number - 1)

The base case, where number is passed the argument 0 or 1, returns 1. The recursive case makes the recursive call factorial(number - 1). Factorial only Since the number argument must be an integer of 1 or greater, the argument to the recursive case gets closer and closer to the base case: 1. In fact, in The Recursive Book of Recursion, I advise that you always ask yourself three questions when writing recursive functions (to which I've provided answers for our factorial() function):

What is the base case? - The base case for factorial() is when number is 0 or 1, and 0! = 1 and 1! = 1 so the base case should evaluate to 1.
What argument is passed to the recursive function call? - In the recursive case, the argument is number - 1.
How does this argument become closer to the base case? - Since number starts off larger than 1, number - 1 ensures it keeps getting smaller until it reaches 1, the base case.

But in case this isn't enough for you to figure out how to write the recursive function, let's use the leap-of-faith technique. First, we start with a blank function:

def factorial(number):
    # Uh... I don't know what code goes here. Leave it blank for now.

Then let's apply the following guidelines:

Start by figuring out the data types of the parameters and return value.

This is easy for factorial. 5! = 120. There is one integer parameter (number) and the function returns an integer.

This is general good advice for writing recursive functions, because the parameters and return value must have consistent data types. You wouldn't want to, say, have factorial() return an integer for the base case and a list of integers for the recursive case. If your recursive function has multiple recursive cases, you wouldn't want one recursive call to pass an integer argument and the other recursive call pass the None value. Make sure you have a firm grasp on what the data types of the parameters and return value are, and make sure your code always sticks to it.

Next, implement the base case.

The base case is usually something small, simple, and has no recursive calls. 1! = 1 is such a base case:

def factorial(number):
    if number == 0 or number == 1:
        # BASE CASE
        return 1

Take a leap of faith and assume your recursive function magically returns the correct value, and write your recursive case.

This means that, before we're done writing our factorial() function, we assume that factorial() always returns the correct value. Wait... that makes it easy! We could just write our function like this:

def factorial(number):
    return factorial(number)

Of course recursion couldn't be this simple. Indeed, if you run this program, you get a stack overflow error:

>>> factorial(10)
Traceback (most recent call last):
  File "<python-input-1>", line 1, in <module>
    factorial(10)
    ~~~~~~~~~^^^
  File "<python-input-0>", line 2, in factorial
    return factorial(number)
  File "<python-input-0>", line 2, in factorial
    return factorial(number)
  File "<python-input-0>", line 2, in factorial
    return factorial(number)
  [Previous line repeated 988 more times]
RecursionError: maximum recursion depth exceeded

This is because there are two important caveats to our magical function:

First Caveat: The argument to the recursive function call cannot be the original argument.

This is a fact that most leap-of-faith explanations fail to mention. This restricts us so that our factorial() function can't simply call factorial(number). Instead, we have to pass some other argument to the recursive factorial() call. After all, "Ten factorial is ten factorial." may be true but it doesn't tell us much. We're forced to think about how factorial(number) can be related to factorial(*something_besides_just_number*).

Earlier, I pointed out that 5! = 5 x 4 x 3 x 2 x 1. If we sit and think for a bit (easier said than done, and this will be different for each recursive algorithm), we can notice that 4! = 4 x 3 x 2 x 1 and then, after more sitting and thinking, 5! = 5 x 4!. As code, this would look like factorial(5) == 5 * factorial(4). But we'd want to generalize this for any argument for the number parameter. We know that factorial(5) == 5 * factorial(4) and factorial(4) == 4 * factorial(3), so it seems the general pattern here is mathematically N! = N x (N - 1)!. As code, this would be return number * factorial(number - 1):

def factorial(number):
    if number == 0 or number == 1:
        # BASE CASE
        return 1
    else:
        # RECURSIVE CASE
        return number * factorial(number - 1)

Ah, if only our magical recursive call to factorial(number - 1) would give us the correct value, then we'd have our solution.

But wait... it does! Or at least, we're taking a leap of faith that it does. But faith is rather useless, so let's try it out and see:

>>> factorial(5)
120
>>> factorial(6)
720
>>> factorial(10)
3628800
>>> factorial(1)
1

It works! Well done! But wait, didn't I say there was a second caveat? There is, and it's one our factorial() function avoided by pure luck:

Second Caveat: The argument to the recursive function call must ALWAYS get closer to the base case.

For the recursive factorial() function we wrote, this is true. The number - 1 argument ensures that the next number argument gets closer to the base case, 1.

This works. We have used the five guidelines of the leap-of-faith technique to write a recursive function. You could stop reading this blog post now.

Or you could keep reading and follow me down a rather strange and demented turn.

What if, instead of having the insight that 5! = 5 x 4!, we noticed that 5! = 6! / 6. Mathematically, this is a correct equation. This would make our recursive case return factorial(number + 1) // (number + 1). (If 5 is our number, we'd generalize this to 6 being number + 1. The integer division operator // ensures we stick with integers and don't get floating-point rounding errors.) And number + 1 is not number, so guideline 4 is being followed. However, by adding to number and making it bigger, we are actually getting further away from the base case, 1.

If we tried to use this code, our factorial() function would look like this:

def factorial(number):
    if number == 0 or number == 1:
        # BASE CASE
        return 1
    else:
        # RECURSIVE CASE - The number + 1 argument gets further away from the base case 1.
        return factorial(number + 1) // (number + 1)

When we run this code, we get a stack overflow:

>>> factorial(5)
Traceback (most recent call last):
  File "<python-input-13>", line 1, in <module>
    factorial(5)
    ~~~~~~~~~^^^
  File "<python-input-12>", line 10, in factorial
    return factorial(number + 1) // (number + 1)
           ~~~~~~~~~^^^^^^^^^^^^
  File "<python-input-12>", line 10, in factorial
    return factorial(number + 1) // (number + 1)
           ~~~~~~~~~^^^^^^^^^^^^
  File "<python-input-12>", line 10, in factorial
    return factorial(number + 1) // (number + 1)
           ~~~~~~~~~^^^^^^^^^^^^
  [Previous line repeated 988 more times]
RecursionError: maximum recursion depth exceeded

Okay, so calling factorial(5) failed. But what if we used a bigger base case? I can figure out 100! by entering the Python expression 100 * 99 * 98 * 97 ... and so on, and that tells me that 100! is 93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000. (This is rather demented.) I'll make this my new base case:

def factorial(number):
    if number == 100:
        # BASE CASE
        return 93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000
    else:
        # RECURSIVE CASE
        return factorial(number + 1) // (number + 1)

And now factorial(5) works, because the argument getting bigger makes it get closer to the base case, 100. It works with all the previous test cases we did:

>>> factorial(5)
120
>>> factorial(6)
720
>>> factorial(10)
3628800
>>> factorial(1)
1
>>> factorial(101)
Traceback (most recent call last):
  File "<python-input-5>", line 1, in <module>
    factorial(101)
    ~~~~~~~~~^^^^^
  File "<python-input-4>", line 10, in factorial
    return factorial(number + 1) // (number + 1)
           ~~~~~~~~~^^^^^^^^^^^^
  File "<python-input-4>", line 10, in factorial
    return factorial(number + 1) // (number + 1)
           ~~~~~~~~~^^^^^^^^^^^^
  File "<python-input-4>", line 10, in factorial
    return factorial(number + 1) // (number + 1)
           ~~~~~~~~~^^^^^^^^^^^^
  [Previous line repeated 988 more times]
RecursionError: maximum recursion depth exceeded

This works as long as the argument passed to factorial() is less or equal to than 100. Unfortunately, calling factorial(101) (or any argument greater than 100) results in a stack overflow. You have to read that fifth guideline carefully, especially the word "always":

The argument to the recursive function call must ALWAYS get closer to the base case.

The factorial() function we wrote with a base case of 100 doesn't ALWAYS get closer to the base case. It only gets closer to the 100 base case when the number argument is less than 100. Well, we can fix this code by only doing return factorial(number + 1) // (number + 1) if number is less than 100. The rest of the time, we can do return number * factorial(number - 1):

def factorial(number):
    if number == 100:
        # BASE CASE
        return 93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000
    elif number < 100:
        # RECURSIVE CASE
        return factorial(number + 1) // (number + 1)
    else:
        # ANOTHER RECURSIVE CASE
        return number * factorial(number - 1)

Now that our code handles number arguments greater than 100 and less than 100, the argument to the recursive function call ALWAYS gets closer to our base case of 100:

>>> factorial(101)
9425947759838359420851623124482936749562312794702543768327889353416977599316221476503087861591808346911623490003549599583369706302603264000000000000000000000000
>>> factorial(5)
120
>>> factorial(102) == factorial(100) * 101 * 102
True

Though perhaps I took this a bit too far.

The Five Guidelines for Taking a Leap of Faith

Start by figuring out the data types of the parameters and return value.
Next, implement the base case.
Take a leap of faith and assume your recursive function magically returns the correct value, and write your recursive case.
First Caveat: The argument to the recursive function call cannot be the original argument.
Second Caveat: The argument to the recursive function call must ALWAYS get closer to the base case.

As long as you follow these five guidelines, you can write a correctly working recursive function. Even if it comes out as demented as that last factorial() function I wrote, the code will work.

Another Example: Recursive Permutation

For all my expertise with recursion, I admit that I still have trouble writing a recursive permutation function. This is a function that is given a string and then returns a set of all permutations (that is, different orderings) of that string. For example, calling permutations('ABC') should return the list ['ABC', 'ACB', 'BAC', 'BCA', 'CAB', 'CBA']. I can never seem to remember how to write this function. I'll follow my own advice and use the four guidelines of the leap-of-faith technique to create it here.

(By the way, the number of permutations for a group of N objects is N!. This is why the factorial of zero is mathematically defined as one; if you have a set of zero objects, there is one way to order the objects in that set: a set of zero objects.)

Start by figuring out the data types of the parameters and return value.

Okay. This is easy. For simplicity, our function will take a single string. The return value will always be a list of strings of the permutations of the string argument. So permutations('ABC') returns ['ABC', 'ACB', 'BAC', 'BCA', 'CAB', 'CBA'], or permutations('AB') returns ['AB', 'BA'].

Next, implement the base case.

Also simple: permutations('') should return the list [''] and permutations('A') should return ['A']. So if the length of the string argument is 0 or 1, the function should return a list of the argument. Remember the data types we set out: permutations() should always return a list of strings like ['A'] and not just a string like 'A'.

def permutations(chars):
    if len(chars) == 0 or len(chars) == 1:
        # BASE CASE
        return [chars]

Take a leap of faith and assume your recursive function magically returns the correct value, and write your recursive case.

Ah, if only we could do this and be done with our problem:

def permutations(chars):
    if len(chars) == 0 or len(chars) == 1:
        # BASE CASE
        return [chars]
    else return permutations(chars)

But we have to keep in mind the fourth guideline:

First Caveat: The argument to the recursive function call cannot be the original argument.

So what can we pass to permutations() instead? Let's sit and think for a bit: To find the permutations of 'ABC', we could split it into the first character (we'll call this the "head") and everything after the first character (the "tail"). We could get all the permutations of the tail, and then inject the head into each position of each permutation. We satisfy the first caveat: when permutations(chars) is called, the recursive case is permutations(chars[1:]) and chars[1:] is different from chars.

Let's think this through with an example. If chars was 'ABC', the head is 'A' and the tail is 'BC'. If we take a leap of faith and assume that permutations('BC') works and returns ['BC', 'CB'], we could go through both these string permutations and make a list with 'A' at each position:

For 'BC', we'd need to create 'ABC', 'BAC', and 'BCA'.
For 'CB', we'd need to create 'ACB', 'CAB', and 'CBA'.

We'd combine this all into one list and return it: ['ABC', 'BAC', 'BCA', 'ACB', 'CAB', 'CBA'].

Okay, I think that would work as long as permutations('BC') works. But does this pass the second caveat?

Second Caveat: The argument to the recursive function call must ALWAYS get closer to the base case.

Well, the tail of the argument to permutations() is always smaller than the argument because it will have one less character. And our base case is when the argument has zero or one characters. So, yes, the argument would always get closer to the base case.

Now we have to actually write the code:

def permutations(chars):
    if len(chars) == 0 or len(chars) == 1:
        # BASE CASE
        return [chars]
    else:
        # RECURSIVE CASE
        all_perms = []  # Start with an empty list.
        head = chars[0]
        tail = chars[1:]

        tail_perms = permutations(tail)
        for perm in tail_perms:  # Go through each of the tail's permutations.
            for i in range(len(perm) + 1):  # Go through each position and inject the head.
                new_perm = perm[:i] + head + perm[i:]
                all_perms.append(new_perm)  # Add it to the complete list of permutations.
        return all_perms  # Return all of the permutations.

Let's take that leap of faith and try it out. Here goes nothing:

>>> permutations('ABC')
['ABC', 'BAC', 'BCA', 'ACB', 'CAB', 'CBA']
>>> permutations('Z')
['Z']
>>> permutations('ABCD')
['ABCD', 'BACD', 'BCAD', 'BCDA', 'ACBD', 'CABD', 'CBAD', 'CBDA', 'ACDB', 'CADB', 'CDAB', 'CDBA', 'ABDC', 'BADC', 'BDAC', 'BDCA', 'ADBC', 'DABC', 'DBAC', 'DBCA', 'ADCB', 'DACB', 'DCAB', 'DCBA']

Hey, it works!

How Does ChatGPT (Fail to) Teach the Leap of Faith Technique (Just Like Every Other Tutorial)?

AI hype continues to annoy me, but I keep an open mind and investigate how useful it is. I gave it the prompt, "Explain the "leap of faith" technique for recursive functions." to see how it would teach the concept. The output was the typical, disappointing tutorial. You can read it if you want, or give it a pass:

The “leap of faith” technique is a way of reasoning about recursive functions that helps you trust the recursion instead of getting tangled up trying to simulate every call in your head.

Here’s how it works:

1. The idea

When you write a recursive function, there are usually two parts:

Base case — a simple, direct answer for the smallest input (no recursion needed).
Recursive case — solve the problem by calling the same function on a smaller or simpler input, then combine that result with some additional work.

The “leap of faith” is the mindset where, once you’ve ensured that the recursive call is on a simpler input and will eventually hit the base case, you assume that it works correctly and returns the right answer — without trying to trace through every smaller call.

2. Why it’s useful

When learning recursion, beginners often get stuck simulating each step:

“Okay, factorial(4) calls factorial(3), which calls factorial(2), which calls… wait, what was I calculating again?”

Instead, the leap of faith says:

“I don’t need to track every call. I’ll assume factorial(3) gives the right answer — because I’ve already made sure it works for smaller inputs — and then I’ll just use that answer to finish factorial(4).”

3. Example: factorial

def factorial(n):
    if n == 0:
        return 1                     # base case
    else:
        return n * factorial(n - 1)   # recursive case

Using the leap of faith for factorial(4):

Base case check: eventually n will be 0, so recursion stops.
Recursive case: assume factorial(3) correctly returns 6 — don’t calculate it in your head — then factorial(4) is 4 * 6 = 24.

4. How to apply the leap of faith

Verify that your recursion moves toward the base case.
Trust that the recursive call returns the correct result for smaller inputs.
Focus only on combining that result to solve the current problem.

5. Why it’s called a leap of faith

You’re “leaping” over the details of how the recursive call works, and having “faith” that it returns the right answer, just like you trust a well-tested library function without reading its source code every time you use it.

If you want, I can also explain how the leap of faith relates to induction proofs — since the reasoning is very similar.

Here are the problems that this, and every other "leap of faith" tutorial has:

No mention on keeping data types consistent. - A common problem beginners have when writing recursive functions, especially for problems like permutations, is having the return value use different data types such as the strings/list of strings example I pointed to earlier. This needs to be made explicit to beginners.
Explicitly pointing out that the recursive call's argument can't just be the original argument. - This is the first thought anyone has when we say, "Assume the recursive function already works." Keep in mind the first caveat (guideline 4): the recursive call argument must be different from the original argument.
Using vague words like "simpler" or "smaller" to describe arguments to the recursive function calls. - What we really mean is that, specifically, the argument in the recursive function call gets closer to the base case. It's not enough to say "smaller", we need to connect it to base case, which also means explicitly writing the code for the base case first (guideline 2 in the list of guidelines I gave.) And keep in mind the second caveat (guideline 5): the argument must always get closer to the base, otherwise you'll end up with a stack overflow.

There's nothing wrong with ChatGPT's explanation; it's technically correct and similar to any other tutorial on the topic. But that's what's wrong with it: students read it, have trouble understanding the vaguely worded concepts, and then assume they just aren't smart enough to understand recursion.

Conclusion

I've always held that recursion isn't a difficult topic so much as it is poorly taught. Many tutorials have a lot of hand-waving and unspoken assumptions, especially for terms like "leap of faith". This tutorial tells you exactly what this term means, along with two caveats you need to keep in mind when using the leap-of-faith technique. If you're interested in learning more about recursion (including drawing pretty fractals and making recursive photos), you can read my free book, The Recursive Book of Recursion or buy a print copy. Good luck!